|
Ente |
Universita’ della Calabria |
|
Struttura |
Facoltà di Ingegneria |
|
Titolo |
Analisi comparativa di alcuni modelli di microsimulazione del traffico stradale |
|
Autore |
Dionesalvi Francesco |
|
Relatore |
Prof. Vittorio Astarita |
|
Correlatore |
|
|
Anno Accad. |
2010 - 2011 |
INDICE
Modelli di simulazione del traffico
1.2 I modelli dinamici di simulazione del traffico
1.3 Dettaglio dei Modelli Microscopici
Il software di microsimulazione INTEGRATION 2.30
2.1 Descrizione del software INTEGRATION 2.30
2.3 Input e Output del modello
2.4 Approccio al modello microscopico
2.5.1 Valutazione della velocità veicolare
2.5.4 Selezione della Rotta e assegnazione del traffico
2.5.5 Modello di Gap Acceptance e segnali di traffico
2.6 Emissioni veicolari di HC, CO e NOx
2.7 Aggregazione delle statistiche sui link e coppie O/D
2.9 Transizione Link-to-Link corsia
2.11 Implementazione e simulazione del software Integration 2.30
2.11.2 File 1: caratteristiche del Nodo
2.11.3 File 2: caratteristiche dell’Arco
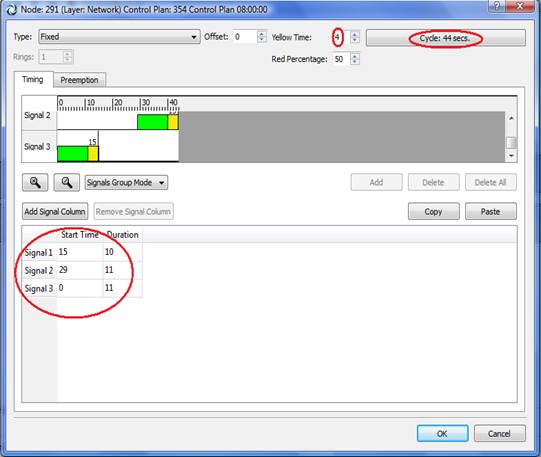
2.11.4 File 3: Piani Semaforici
2.11.6 File 4: domande di traffico Origine/Destinazione
2.11.7 File 5: Incidenti o blocchi di corsia
2.11.8 Modello Output fondamentale
Il software di microsimulazione
3.1 Descrizione del software SUMO TRAFFIC
3.4 Caratteristiche del software
3.5 Modello alla base di Sumo Traffic
3.5.1 Comportamento del veicolo
3.5.2 Lane-Changing e Car-Following
3.7 Caratteristiche aggiuntive
3.9 Elementi aggiuntivi di Sumo Traffic
3.11 Preparazione della simulazione
Il software di microsimulazione AIMSUN 6.1
4.1 Il modello microscopico alla base di AIMSUN
4.1.1 Modello di Car Following
4.1.2 Calcolo della velocità di un veicolo in una sezione
4.1.3 Il modello di car-following nel caso di doppia corsia
4.1.4 Calibrazione del modello di car-following
4.1.5 Modello di Lane-Changing
4.1.6 Il Modello Gap Acceptance di AIMSUN
4.2 Implementazione e simulazione
4.2.6 Assegnazione del tipo di strada alle sezioni
Il software di microsimulazione Tritone
5.1 Il modello alla base di Tritone
5.3 Organizzazione dell’area di lavoro
5.4 Creazione di una rete stradale
5.4.1 Inserimento e modifica dei nodi della rete
5.4.2 Inserimento e modifica degli archi della rete
5.4.3 Inserimento e modifica dei flussi veicolari sulla rete
5.4.4 Inserimento e modifica incidenti o cantieri sulla rete
5.4.5 Inserimento e modifica dei semafori sulla rete
5.5 Modifica dei parametri dei modelli
La scienza non è altro che percezione.
Non si possono concepire i molti senza l'uno.
(Platone per bocca di Socrate, Gorgia)
La linea filosofica del realismo matematico, proposta da Platone, afferma l’esistenza di un livello di razionalità del tutto distaccato dalle percezioni, dalle entità fisiche, dalla mutevolezza e arbitrarietà delle opinioni. Proprio come gli oggetti materiali sono visti dai sensi, gli oggetti matematici come numeri e forme possono essere osservati attraverso il pensiero astratto, rivelando attributi oggettivamente verificabili. Nessun uomo potrà mai dubitare che un triangolo sia quella figura la somma dei cui angoli è uguale a 180 gradi. Ma questa verità eterna ed universale non si riferisce al triangolo ‘materiale’, tracciato sulla carta, che è sempre imperfetto, bensì soltanto al suo modello, appunto l’idea di triangolo, che può venire soltanto colta con il pensiero e non percepita con i sensi. I concetti matematici, pertanto, sono "reali" quanto gli oggetti concreti, solamente invisibili ai sensi esterni come il suono è impercettibile all'occhio.
La simulazione su computer ci porta a riscoprire il realismo matematico. La mente di Platone poteva considerare solo oggetti matematici semplici, portandola a dicotomie come l'idea di una sfera perfetta contro la palla di marmo imperfetta e graffiata. La simulazione elettronica, come un telescopio per la mente, estende la nostra visione oltre il regno dei semplici oggetti, a dettagli di mondi lontani, alcuni tanto complessi quanto la realtà fisica.
Il nostro stesso mondo appartiene a questa gamma di tutti i mondi possibili, definiti dalle relazioni astratte che chiamiamo leggi della fisica, come ogni simulazione è definita dalle sue regole interne.
In La Repubblica, Platone afferma, sempre per bocca di Socrate:
“Nella ricerca dell’intellegibile, l’anima è costretta a ricorrere a ipotesi, senza arrivare al principio, perché non può trascendere le ipotesi; essa si serve, come d’immagini, di quegli oggetti stessi di cui quelli della classe inferiore sono copie e che in confronto a questi ultimi sono ritenuti e stimati evidenti realtà.”
La differenza tra la realtà fisica e la realtà matematica è quindi un’illusione data dal nostro punto di vista: il mondo reale è semplicemente il mondo astratto che ci contiene.
Renè Descartes concorda con Platone che il mondo che percepiamo attraverso i sensi potrebbe essere un’elaborata messinscena. Nel diciassettesimo secolo, Descartes postulò un improbabile demone, capace di creare un’esistenza illusoria controllando tutto quello che vediamo e sentiamo. Oggi la tecnologia della realtà virtuale ci ha fornito questo potere. L’uomo, cibernauta entusiasta, utilizza visori e fili collegati ad appositi sensori per brevi immersioni in mondi immaginari, basati su meccanismi fondamentali completamente differenti dai campi quantici che, le ultime teorie suggeriscono, costituiscono il nostro mondo fisico. L’esploratore virtuale contemporaneo però non trascende del tutto dal mondo reale: se colpisce un oggetto vero, sente dolore vero.
Fino a che punto sarà possibile indebolire questo collegamento?
Riusciremo in futuro a connettere tutti i nervi periferici del cervello ad un elaborata simulazione non solo del mondo circostante, ma anche di un corpo che lo ospiti?
Sarà forse possibile confezionare il cervello in una scatola, come quelle che troviamo sugli scaffali dei supermercati, e spezzarne tutti i legami con il mondo esterno implementando il cervello stesso come simulazione?
Se parti del cervello danneggiate o in pericolo, proprio come il corpo, potessero essere rimpiazzate da simulazioni equivalenti, alcuni individui potrebbero sopravvivere alla distruzione fisica totale, e ritrovarsi vivi sotto forma di pura simulazione elettronica, in mondi virtuali.
Una siffatta ipotesi apre la strada ad un inquietante pensiero: un mondo simulato ospitante una persona simulata costituisce un’entità autocontenuta. Tutto ciò potrebbe esistere come programma su un computer che elabora silenziosamente dati in qualche angolo oscuro, senza dare segni esterni di gioie e dolori, di successi e frustrazioni. Dentro alla simulazione, invece, gli eventi si susseguirebbero secondo la rigida logica del programma, che definirebbe le leggi della fisica all'interno di tale simulazione. L'abitante potrebbe, attraverso paziente ricerca e deduzione, elaborare qualche rappresentazione delle leggi della simulazione, ma non inferire la natura, e nemmeno l'esistenza del computer simulatore.
Le simulazioni di oggi, come ad esempio quelle del traffico sulle reti stradali, vengono utilizzate per ottenere risposte ed immagini, attraverso programmi aggiuntivi che traducono le rappresentazioni interne della simulazione in forme convenienti per noi, osservatori umani esterni. Il presente lavoro, in particolar modo, è incentrato sullo studio e l’analisi di quei processi che implementano, o codificano, la microsimulazione del traffico veicolare.
Un qualcosa è chiaramente un codice se esiste una maniera di decodificarlo, o tradurlo, in qualche forma della simulazione che sia riconoscibile. I software che producono immagini di auto in movimento, o viste di intersezioni stradali, nel caso dei simulatori del traffico, sono esempi di tali decodificazioni.
La relazione tra gli elementi all'interno della simulazione e la loro rappresentazione esterna potrebbe essere talmente complicata da rendere il processo di decodificazione proibitivo. Ma non esiste un limite ben definito. Una traduzione che è impossibile oggi potrebbe essere possibile domani, con computer più potenti o mediante qualche approccio matematico finora sconosciuto.
L'interpretazione di una simulazione è infatti solo un rapporto matematico tra i passi di una simulazione e visualizzazioni della stessa, che abbiano senso per un particolare osservatore. Per rendere possibile l'interpretazione potrebbe essere sufficiente un piccolo e veloce programma, ma matematicamente, l'interpretazione potrebbe anche richiedere una gigantesca tabella, che contenga una visuale dell'osservatore per ogni stato del processo. Ma se è vero che esiste sempre una possibile tabella che traduca qualunque situazione allora, non solo i supercomputer, ma qualunque cosa può essere in teoria considerata una simulazione di ogni mondo possibile! L’uomo pertanto, è capace di cogliere solo una porzione infinitesimale dell'infinità di possibili mondi, tuttavia, una porzione sempre maggiore sarà potenzialmente visibile, all’aumentare della nostra abilità nel manipolare i dati. È probabile che i nostri discendenti superintelligenti saranno in grado di compiere passi interpretativi sempre più grandi, spingendosi oltre l’immaginabile. A noi, oggi, soldati della ragione, armati dalla razionalità matematica, non ci resta che affidarci a Socrate, nostro generale, e chiedergli di condurci attraverso il mondo dei modelli ideali, al fine di ricercare quelle verità universali e perfette che stanno anche alla base dei “modelli di microsimulazione del traffico stradale”.
Negli ultimi decenni la mobilità ed il traffico sono diventati temi di grande attualità. L’auto è diventata il mezzo preferenziale per fasce di mercato sempre più vaste, a causa dei cambiamenti subiti dalla domanda di trasporto non solo in termini quantitativi, ma anche riguardo alla sua struttura temporale e spaziale. Tutto questo non è stato accompagnato da una corretta pianificazione dei sistemi di trasporto, che sarebbe servita per giungere ad un equilibrio territoriale e di ripartizione modale. Di conseguenza, le strade sono state portate ai limiti della capacità, e, maggiori e sempre più frequenti, sono diventati i fenomeni di congestione che peggiorano le prestazioni delle reti stesse. Le congestioni che si possono verificare hanno una forte caratterizzazione temporale, infatti sono fenomeni che si presentano in particolari momenti del periodo di osservazione. Per esempio, se analizziamo delle situazioni relative ad intersezioni che si trovano nei pressi di edifici scolastici vedremo che la maggiore affluenza si avrà all’orario di ingresso e di uscita degli studenti dalla struttura scolastica. Ci sono molti altri esempi che potrebbero essere proposti come quello dei centri commerciali, o come la riduzione della capacità della strada a causa di un incidente o di un cantiere presente sulla carreggiata.
Per una giusta valutazione di questi fenomeni sono necessari degli strumenti adeguati che, oltre a collocare spazialmente il fenomeno, ne descrivano i suoi effetti nel tempo, considerando il momento di inizio e la sua evoluzione, al variare del tempo e delle condizioni di traffico. A tal proposito, i modelli di assegnazione dinamica del traffico o modelli DTA (Dynamic Traffic Assignment), hanno trovato un largo impiego, quali strumenti analitici per la simulazione e l’analisi quantitativa dei fenomeni caratteristici di una rete di trasporto.
I modelli dinamici di simulazione del traffico vengono utilizzati in ambito progettuale, per poter effettuare valutazioni sia in fase di realizzazione che di collaudo dei progetti. Essi permettono di rappresentare su scala ridotta, e, quindi, ad un costo relativamente basso, gli effetti e le conseguenze relativi allo sviluppo di un nuovo progetto (una strada, un’area di parcheggio, un ponte, ecc). Negli ultimi tempi le potenzialità di questi modelli che simulano le condizioni più varie del traffico si sono sempre più perfezionate. In generale, la modellazione e la simulazione matematica si sono rivelate uno strumento valido, sempre più utilizzato, per l'analisi di un numero sempre maggiore di problemi.
1.2 I modelli dinamici di simulazione del traffico
I metodi di simulazione tradizionale si basano sull’ipotesi di stazionarietà intraperiodale. Si valuta cioè la domanda di trasporto,assunta in termini di valore medio nel periodo considerato, su un intervallo sufficientemente lungo tale da poter considerare le condizioni come stazionarie.
Nella realtà, affinché il sistema possa raggiungere la condizione di funzionamento stazionario, domanda, scelta di percorso e sistema di offerta dovrebbero rimanere costanti per tutto il periodo di tempo necessario al raggiungimento di tale condizione. In tal caso l’invarianza nel tempo delle variabili che descrivono il funzionamento del sistema di trasporto, consente di darne una rappresentazione mediante un’unica fotografia; una rappresentazione che potremmo pertanto definire statica. Tuttavia, le semplificazioni, indotte da tale assunzione di stazionarietà, non consentono di rappresentare il funzionamento interno del sistema. Pertanto, non possono essere considerati tutti quei fenomeni dinamici che caratterizzano le reti congestionate: la propagazione del ritardo a ritroso, la formazione di code e la loro evoluzione e dissipazione, gli effetti di un incidente sulla rete stradale, la variazione della domanda nel tempo e le prestazioni della rete nel caso di fenomeni eccezionali come, per esempio, l’evacuazione di alcune aree a causa di calamità naturali.
Chiaramente fenomeni di questo tipo non possono essere studiati in termini di valori medi, perché proprio la variabilità della domanda e di altre caratteristiche porta alla formazione di ulteriori fenomeni di congestione. Basti pensare, per esempio, ad una rete sulla quale, in un particolare momento del periodo di osservazione, la domanda supera la capacità dell’infrastruttura con il conseguente verificarsi di rallentamenti ed, in alcuni casi, di arresto dei veicoli. Tuttavia, se il valore della domanda rilevato durante il periodo di osservazione viene espresso in termini medi, non è possibile mettere in luce il fenomeno che porta alla situazione critica prima descritta. Quindi l’obiettivo dei modelli dinamici è proprio quello di considerare la variazione del flusso nel tempo per rilevare le situazioni di criticità che sarebbero altrimenti non evidenziabili con l’utilizzo di strumenti statici.
I primi modelli dinamici del deflusso stradale, proposti negli anni cinquanta del secolo scorso, fornivano una rappresentazione del deflusso stradale basata su di un’analogia con il deflusso idrico. In tale approccio i singoli veicoli sono trattati come un fluido continuo (mono-dimensionale), per il quale possono definirsi in ciascun punto dello spazio e del tempo variabili quali la portata, la densità e la velocità. La rete stradale viene considerata come una rete di incanalamenti percorsa dai flussi di traffico. Le caratteristiche dei tronchi della rete (capacità,velocità medie, ecc.) e la domanda di mobilità (volume di traffico, origine destinazione dei veicoli, ecc.) determinano il modo in cui la rete viene percorsa da tali flussi. Nel tempo le variabili di stato, sono state modellate attraverso un’equazione alle derivate parziali che comprende tanto la conservazione della massa (i veicoli) quanto una relazione sperimentale tra flusso e densità.
Sebbene siano ormai diversi anni che gli esperti di mobilità si dedicano a modelli di comportamento dinamico, solo negli ultimi tempi la ricerca si è indirizzata verso il comportamento dinamico del traffico nell’ambito della modellizzazione e assegnazione dello stesso nell’intero sistema di rete.
La maggior parte degli studi di settore hanno proposto dei modelli dinamici di assegnazione del traffico : Dynamic Traffic Assignment . I modelli DTA servono a determinare il modello di traffico della rete nel tempo come conseguenza delle interazioni dinamiche dell’offerta e della domanda. Le proprietà di questi modelli hanno implicazioni importanti sulla pianificazione del traffico e dipendono fortemente da due componenti:
- la scelta del percorso da parte dell’individuo
- la componente traffico-flusso
La scelta del percorso incorpora al suo interno il comportamento degli utenti, cioè il modo con il quale un individuo autonomamente decide le rotte, l’orario di partenza o le destinazioni. L’altra componente descrive come il traffico si propaga all’interno di una rete di trasporto e perciò controlla la performance della rete in termini di tempi di percorrenza.
Il settore della modellistica è molto vasto ed in continuo sviluppo. L’interesse per la creazione di applicazioni matematiche, cioè modelli e algoritmi che descrivano l’ambiente operativo (rete e offerta), nonché l’utenza, con le sue esigenze (domanda), hanno portato alla formulazione di diverse teorie con risultati anche discordi. Sulla base di queste teorie sono stati realizzati e implementati svariati software di simulazione a supporto delle diverse strategie di pianificazione dei trasporti. Questi modelli variano per approccio teorico, metodo di assegnazione, gestione delle casualità ed interfaccia grafica, nonché nel livello di dettaglio che descrive lo scenario. I modelli possono essere classificati basandosi, da un lato sulla rappresentazione del flusso di utenti (continua o discreta), e dall’altro sulle funzioni di prestazioni adottate (aggregate o disaggregate). Secondo una classificazione generalmente condivisa è possibile distinguere tre importanti approcci alla simulazione.
|
|
Funzioni di prestazioni |
|
|
Rappresentazione del flusso |
Aggregate |
Disaggregate |
|
Continua |
macroscopici |
|
|
Discreta |
mesoscopici |
microscopici |
Tabella 1.1: Approcci alla simulazione (Rivadossi, 2004), in [1].
La tabella 1.1 presenta una classificazione di modelli di deflusso veicolare non stazionari per sistemi continui. La scelta del modello da utilizzare dipende naturalmente dal livello di dettaglio richiesto dall’applicazione; per questo motivo bisogna tenere conto che ogni tipologia di modello (micro, macro e meso) presenta delle difficoltà di raccolta dei dati e di costruzione del modello stesso.
Appartengono alla prima categoria, i modelli di macrosimulazione (detti anche “di prima generazione”). Essi considerano il traffico nella sua totalità, descrivendolo come un flusso definito da regole comportamentali incentrati principalmente sull’interazione dei veicoli tra di loro e con l’infrastruttura. I modelli macroscopici (modelli aggregati) si basano sulla simulazione continua del traffico, concentrandosi perlopiù sul traffico nella sua evoluzione, fornendo previsioni sulla velocità media di scorrimento, sul flusso e sulla densità veicolare (grandezze continue e mediate) (Ortúzar e Willumsen, 1995), in [2]. Pertanto in questo tipo di modellazione non viene seguito direttamente il singolo veicolo, come avviene nei modelli microscopici dove si valutano direttamente le traiettorie veicolari, ma semplicemente l’evolversi continuo dell’intero flusso veicolare. Tali modelli, quindi, si possono classificare in base alla loro rappresentazione dello spazio, assumendo continuo il tempo (Cascetta, 2006),in [3], e pertanto sono anche detti modelli continui nel tempo e nello spazio. I modelli a spazio continuo si basano su variabili definite in ogni punto dello spazio; soluzioni analitiche di questi modelli sono state fornite per schemi molto semplici mentre, situazioni più complesse richiedono una soluzione numerica ottenuta attraverso una discretizzazione spazio/temporale. I modelli a spazio discreto sono invece più prossimi ai modelli statici: le variabili di base, che influenzano la prestazione del ramo (densità e velocità), sono definite a livello dell’intero ramo; la loro soluzione richiede solitamente una discretizzazione temporale.
La teoria matematica, alla base dei modelli di macrosimulazione, rappresenta il traffico stradale come un fluido continuo e affida la simulazione del traffico ad alcune equazioni differenziali che esprimono le leggi di conservazione del flusso. Il vantaggio principale, legato all’utilizzo di questa tipologia di modello, è connesso al fatto che in fase di formulazione del problema è possibile effettuare una rappresentazione più compatta e generica, tutto ciò determina però un elevato grado di difficoltà nel rappresentare fenomeni di formazione di code o casi di sovrasaturazione del sistema.
I modelli mesoscopici, si collocano tra l’approccio aggregato dei modelli macroscopici e quello più particolare dei modelli microscopici riferito al singolo elemento. Essi consentono di avere un livello di rappresentazione più dettagliato rispetto ai modelli macroscopici, nonostante le prestazioni della rete vengano simulate a livello aggregato, utilizzando variabili quali la capacità, il flusso, la densità, etc. Questi modelli concentrano l’attenzione sul comportamento di gruppi di utenti e gli output che si ottengono sono riferiti appunto a tali gruppi e non ai singoli veicoli (come nella microsimulazione). Ogni singolo insieme (detto “pacchetto”) è composto da veicoli che hanno la stessa origine, la stessa destinazione e la stessa strategia di scelta (percorso, velocità, etc.) durante il loro movimento. Di questi gruppi, si simula lo spostamento rigido seguendone la traiettoria nello spazio; quanto più piccola è la dimensione del gruppo, tanto più la soluzione del modello è vicina al tipo microscopico. Attraverso l’utilizzo dei suddetti modelli, è possibile rappresentare numerosi fenomeni di tipo dinamico, tra cui sovra saturazione, formazione e propagazione di code, ma, non è altresì possibile simulare alcuni fenomeni di deflusso quali i sorpassi, i cambi di corsia ed altri.
Si parla di microsimulazione, se si desidera ricostruire l’evoluzione del traffico studiando la singola unità. Nello specifico, i modelli di microsimulazione (modelli disaggregati) simulano il movimento e le traiettorie dei singoli veicoli, consentendo di rappresentare in maniera puntuale, precisa e specifica il traffico e la sua evoluzione, istante per istante. A tal proposito, si dovranno tenere in considerazione gli aspetti geometrici di dettaglio dell’infrastruttura nonché il comportamento reale del conducente, legato all’accoppiamento delle caratteristiche del veicolo e del guidatore. In sostanza tali modelli di simulazione, rappresentano il traffico stradale ad un livello di dettaglio molto elevato. Permettono di simulare lo spostamento di ogni veicolo della rete (rappresentazione della velocità, dell’accelerazione, etc.) e tutte le sue interazioni con gli altri veicoli della rete (sorpassi, cambi di corsia, etc.). Fra tutti i modelli di simulazione, i microscopici, sono quelli che consentono un maggiore dettaglio significativo, tuttavia essi presentano, anche, un livello di complessità molto elevato. Infatti, solo recentemente, grazie all’incremento delle potenzialità computazionali, i modelli di microsimulazione sono diventati mezzi di analisi interessanti, in grado di lavorare con un’elevata risoluzione sia temporale che spaziale. Tuttavia, vista l’elevata quantità di dati che tali modelli richiedono e producono, (basti pensare a simulazioni dove si considerano le attività giornaliere di più di un milione di persone) è possibile applicarli generalmente a reti di dimensioni ridotte, per le quali non è necessario impegnare notevoli risorse di calcolo sia in termini di memoria disponibile che di velocità di esecuzione. In Figura 1.1 si riporta una raffigurazione riassuntiva dei diversi approcci alla simulazione.
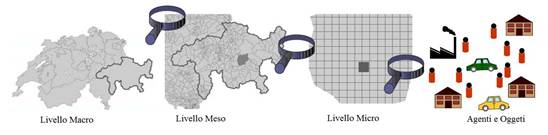
Figura 1.1: Risoluzione spaziale dei diversi approcci alla simulazione (versione adattata Schwarze et al., 2004), in [4].
Negli ultimi anni sono stati realizzati una quantità significativa di lavori al fine di aumentare la qualità e l’accuratezza dei modelli di simulazione del deflusso veicolare. Molti di questi lavori hanno interessato modelli nati dalla necessità di rappresentare l’interazione tra i singoli veicoli. Il moto dei veicoli si ottiene come risultato di scelte disaggregate individuali e delle interazioni con gli altri mezzi presenti sulla rete. La scelta del percorso, le decisioni di accelerare o di cambiare corsia, il comportamento alle intersezioni di ogni singolo veicolo vengono esplicitamente modellate. Ogni veicolo inoltre possiede le proprie caratteristiche relative, ad esempio, alle prestazioni dei singoli mezzi (l’accelerazione massima o la velocità) o alle caratteristiche dei guidatori (il tempo di reazione o la velocità desiderata). I modelli microscopici solitamente considerano la coppia formata dal veicolo e dal suo guidatore come un unico elemento e non separano quindi il processo decisionale del guidatore dal controllo del veicolo. La ragione principale alla base di questa scelta è dovuta al fatto che questi modelli sono stati messi a punto e vengono tuttora utilizzati principalmente con lo scopo di analizzare i sistemi di traffico. Di solito il comportamento dei flussi di traffico viene riprodotto come risultato dell’interazione tra i guidatori, in maniera tale da ottenere una rappresentazione realistica delle dinamiche del deflusso veicolare. Anche se i modelli sono disaggregati, in quanto riproducono il moto dei singoli veicoli, sono spesso utilizzati per analisi aggregate (flussi, lunghezze di coda, tempi di percorrenza, etc.). Ogni tipologia di modello (micro, macro e meso) presenta delle difficoltà nella raccolta dei dati e nella costruzione del modello stesso. Inoltre il problema dinamico di caricamento della rete dipende principalmente dalla complessità di riprodurre lo stato dinamico del traffico, ed è accentuato dal fattore umano insito nel comportamento degli utenti. La corrente di traffico su una rete è determinata da un insieme di regole che variano a seconda del modello utilizzato. Questa corrente è definita come il flusso q(t) (1.1) attraverso un punto della sezione S della strada:
(1.1)
Un metodo elementare per la modellizzazione dell’arco, per una singola destinazione, è composto dal sistema di equazioni differenziali 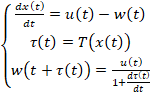(1.2):
(1.2)
dove ogni arco al tempo t ha le seguenti caratteristiche: flusso a monte u(t), flusso a valle w(t) e numero totale di utenti x(t) sull’arco; dove x(t), u(t) e w(t) sono funzioni continue nel tempo mentre τ(t) è il tempo di viaggio rispetto a t (tempo di viaggio della porzione che entra nell’arco al tempo t). Il modello (1.2) è stato ampliato per riprodurre il fenomeno del blocco delle intersezioni a monte (spill-back delle code) e il modello analitico proposto è quello più elementare che riesce a riprodurre tale fenomeno. Di seguito verranno analizzati, nel dettaglio, i modelli di simulazione microscopici.
1.3 Dettaglio dei Modelli Microscopici
I modelli microscopici descrivono i movimenti dei singoli veicoli come il risultato di scelte individuali disaggregate e delle interazioni con gli altri veicoli e con l’ambiente. La scelta del percorso, le decisioni di accelerazione o cambio corsia, il comportamento alle intersezioni etc., di ciascun veicolo, sono in generale modellizzati esplicitamente. Pertanto, oltre a fornire tutti gli elementi per una dettagliata analisi quantitativa, variazioni dei tempi di percorrenza, durata delle code, consumi di carburante, emissioni di inquinanti, etc., i modelli di microsimulazione consentono di visualizzare in maniera realistica il movimento dei singoli veicoli, moto, auto, furgoni e mezzi pubblici nonché l’evoluzione del traffico sulla rete stradale. Per tutte queste ragioni essi risultano essere lo strumento più aggiornato per la valutazione degli effetti di scelte progettuali e di regolazione sulla rete di trasporto stradale sia su scala locale che su quelle più ampie.
Le possibilità di applicazione di un modello Microscopico, pertanto, sono molteplici: la progettazione di nuove infrastrutture (strade, rotatorie, svincoli, ecc.), sistemi di controllo semaforico, corsie riservate, sensi unici di marcia, zone a traffico limitato, ecc.
Questi modelli inoltre, sono in grado di simulare eventi eccezionali (incidenti, cantieri di lavoro, ecc.) i quali provocando una temporanea limitazione della capacità delle sezioni stradali, potrebbero limitare in modo assai rilevante le condizioni del traffico veicolare. L’approccio utilizzato da questi modelli è di tipo micro, poiché durante tutto l’intervallo di analisi, il comportamento di ogni singolo veicolo viene simulato sulla base di algoritmi decisionali di tipo comportamentale, i quali stabiliscono, di volta in volta, il cambio di corsia, regolano la distanza dal veicolo che precede l’immissione nelle corsie di accelerazione e decelerazione, i sorpassi, etc.. La scelta del percorso stesso viene, periodicamente, calcolata in funzione delle mutate condizioni della rete (presenza di congestione o di un eventuale impedimento alla circolazione). Ogni aggiornamento viene ottenuto dal guidatore considerando la propria velocità ed accelerazione e tenendo presente la situazione del traffico che lo circonda. Infatti in questi modelli, si considera che la posizione del veicolo al tempo t+∆t dipende dalla posizione e dalla velocità tenuta dal guidatore al tempo t. Quest’ultima grandezza, invece, viene definita da ulteriori fattori, che dipendono dal veicolo considerato e da quello immediatamente davanti; fattori significativi sono perciò la distanza, la velocità relativa, il tempo di reazione dell’autista, in relazione al gap dal veicolo che lo precede e alla velocità di quest’ultimo, e infine, la presenza di altri veicoli nelle corsie adiacenti.
L’aggressività e lo stile di guida dei conducenti possono influenzare l’andamento della simulazione, in quanto i guidatori, “molto abili” o “aggressivi”, hanno tempi di reazione più brevi degli altri; essi possono guidare vicino ai veicoli precedenti, trovare intervalli di accesso più rapidamente e facilmente, accelerare e frenare repentinamente. Tutti questi elementi fanno in modo che il modello si avvicini il più possibile alla realtà.
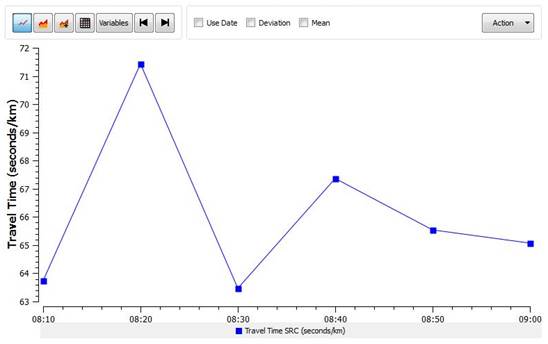
L’applicazione di un modello microscopico produce sia risultati di tipo grafico che di tipo statistico. Dal punto di vista grafico gli attuali sistemi software permettono di ottenere animazioni tridimensionali e bidimensionali, che rappresentano le condizioni istantanee della rete, i diagrammi di visualizzazione della velocità di percorrenza, dei veicoli in coda, etc. I risultati di tipo statistico, che si possono ottenere, riguardano principalmente i flussi, la velocità media, il tempo di viaggio, la differenza tra il tempo di viaggio effettivo e il tempo che occorrerebbe per compiere il tragitto in condizioni ottimali, il numero di volte che i veicoli si fermano, il tempo trascorso in coda, le lunghezze delle code, etc. Le statistiche sono relative alla rete stradale nel suo complesso, a porzioni di essa, a determinati percorsi o a singole sezioni stradali. Il modello fornisce, inoltre, statistiche relative al consumo di carburante ed alle emissioni dei principali inquinanti.
I software di microsimulazione basano il loro funzionamento su modelli in grado di rappresentare singolarmente il movimento di ciascun veicolo sulla base del comportamento del conducente, che segue le regole, dettate dalla teoria dell’inseguitore “Car-Following”, da quella del cambio corsia “Lane-Changing” e da quelle dell’intervallo minimo di accesso “Gap-Acceptance”.
I modelli car following si basano sull’idea, che ogni veicolo si muove lungo una strada seguendo il veicolo che lo precede, e perciò la sua dinamica è funzione solo di quel veicolo. Questa ipotesi risulta di semplice modellazione matematica, anche se è relativamente poco complessa se confrontata con la totalità dei comportamenti che si tengono durante la guida. I modelli microscopici, in linea generale, assumono la forma riportata nella 1.3.
(1.3)
nella quale:
- 
è
la distanza effettiva tra il veicolo e il suo predecessore tenendo in
considerazione la lunghezza del veicolo;
- v(t) e x(t) rappresentano la velocità e la posizione del veicolo al tempo t;
- 
rappresentano
la velocità e la posizione del veicolo che precede quello considerato;
- ∆t è il tempo di campionamento;
- ξ(t) è un componente stocastico di rumore inserito nel modello. Ogni guidatore, infatti è un’entità autonoma, dotata di un suo modo di agire e di tempi di reazione diversi;
- p è il vettore delle componenti parametriche del modello.
Il modello può essere schematizzato come in Figura 1.2:
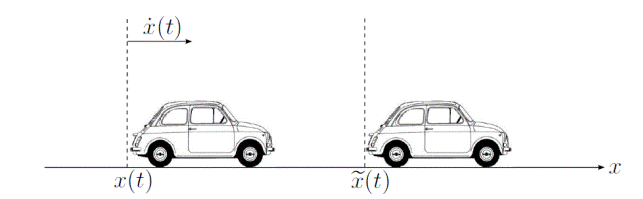
Figura 1.2: Schema del modello car-following.
Nei modelli di car
following, introdotti per la prima volta attorno alla metà del secolo scorso e
attribuibili a Reuschel e Pipes [5][6], si assume che ogni guidatore tende a
muoversi con la stessa velocità del veicolo che lo precede. Se si considera,
quindi, un tratto di strada fissato, ogni macchina occuperà una posizione 
e
una lunghezza 
.
Posti 
e
,
rispettivamente la posizione del veicolo che precede e quella del veicolo
considerato, è possibile determinare la velocità 
e
l’accelerazione 
del
veicolo 
.
Quest’ultima risulta essere funzione della velocità del veicolo stesso e di
quello che lo precede.
(1.4)
dove la funzione 
sarà
scelta nel rispetto dei parametri essenziali al fine di rispecchiare al meglio lo
scorrimento del traffico. Secondo Pipes e Reuschel, l’equazione che descrive il
moto della coppia dei veicoli è la seguente:
(1.5)
Da ciò si evince che ogni automobilista
mantiene una distanza di sicurezza, funzione della propria velocità e della
distanza 
,
relativa
alla lunghezza dell’auto che lo precede (Figura 1.3).
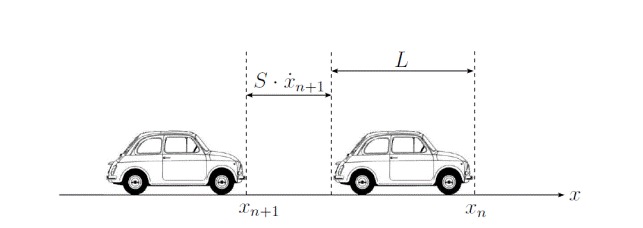
Figura 1.3: Il modello di Pipes
Derivando l’equazione 1.5 otteniamo:
(1.6)
dove il rapporto ( 
)
viene detto fattore di sensibilità.
L’equazione (1.6) è la formula generale del modello lineare Follow the leader (uno degli approcci del metodo car following), proposta per la prima volta dall’americano Chandler [7].
Dal momento che
l’automobilista non risponde istantaneamente agli stimoli esterni, è stato
introdotto un ritardo 
,
in funzione del quale è possibile riscrivere l’equazione (1.6) come segue:
(1.7)
Tale relazione è anche nota come l’equazione di base dei modelli car following.
Al fine di ottenere risultati più accurati, è consigliabile esprimere il fattore λ in funzione di ogni guidatore:
(1.8)
dove 
è
una costante ed l e m sono esponenti interi.
Il modello proposto da Reuschel e Pipes, considerato uno dei migliori tra quelli microscopici, fu approvato nel 1958 da Chandler e altri ricercatori grazie ai dati forniti dal General Motors Technical Center.
1.3.1.1 Il Modello di Gipps
Il modello di Gipps[8] appartiene alla categoria dei car following e consiste in due componenti separate di accelerazione e decelerazione. La prima componente, rappresenta il proposito di un dato veicolo di raggiungere una velocità desiderata v* in accordo con le caratteristiche del veicolo stesso; la seconda equazione riproduce la limitazione sulla velocità imposta dal veicolo immediatamente precedente.
Queste due condizioni, possono essere formulate come in (1.9), dove la prima equazione modella la dinamica del veicolo in condizioni di flusso libero, mentre la seconda modella l’interazione con il veicolo che lo precede.
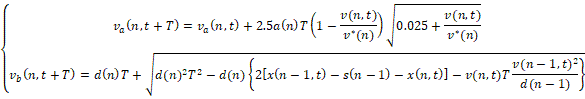(1.9)
- n indica l’n-esimo veicolo,
- 
è
la velocità desiderata dell’n-esimo veicolo,
- a(n) e d(n) sono la massima accelerazione e decelerazione possibile per il veicolo,
- d(n–1) è la massima decelerazione possibile per il veicolo che precede l’n-esimo,
- x(n-1, t) e x(n, t) sono rispettivamente la posizione al tempo t del veicolo (n–1)-esimo e di quello che lo segue,
- v(n-1,t) e v(n, t) sono le velocità al tempo t dei due veicoli,
- T è il tempo di campionamento dal quale derivano le prestazioni del modello e che quindi va fissato in base al caso specifico. In genere, 0≤T≤1.25 secondi, ma ciò dipende molto dal tipo di strada.
Il modello dinamico che si ricava dalle (1.9) è quindi:
(1.10)
Il modello di Gipps permette di simulare la dinamica di ogni singolo veicolo, che risulta essere condizionata dalle interazioni con il veicolo che lo precede.
L’inconveniente maggiore, che però si può riscontrare, è la difficoltà nel reperire le informazioni relative alla massima accelerazione e decelerazione dei veicoli e alle caratteristiche dei guidatori. Tuttavia il modello di Gipps, grazie anche ad alcune rettifiche che ne semplificano l’impiego, è attualmente uno dei più usati e dei più accurati tra i modelli microscopici. Esso è preso come riferimento anche dal simulatore del traffico AIMSUN2.
Le modifiche riguardano:
- il
calcolo di ,
- l’influenza dei veicoli della corsia adiacente sulle decisioni del veicolo, nel caso di multi corsia,
- l’effetto della salita e della discesa della rete stradale.
Il primo miglioramento è
legato alla velocità desiderata. Il calcolo di è
funzione di tre parametri:
1. la
velocità massima desiderata 
,
2. il
limite massimo di velocità per il tratto di strada s preso
in esame, 
,
3. il rispetto dei limiti di velocità da parte del guidatore, Ө(n). Tale parametro può essere scelto attraverso una distribuzione di probabilità, che partendo da osservazioni reali riproduce il grado di aggressività dei guidatori. In particolare:
a) se Ө(n)<1, il guidatore viaggia ad una velocità inferiore rispetto ai limiti di velocità,
b)
se
Ө(n)=1,
il guidatore viaggia ad una velocità pari a ,
c) se Ө(n)>1, il guidatore non rispetta il limite di velocità.
La formula per calcolare la velocità desiderata diventa:
(1.11)
essendo:
(1.12)
Il secondo miglioramento
si basa sull’ipotesi che anche i veicoli della corsia adiacente possono influenzare
la velocità del veicolo n-esimo.
Se la corsia adiacente è una corsia di decelerazione, si indica con 
la
differenza massima di velocità tra il veicolo n-esimo e
gli altri veicoli che si trovano nella corsia di accelerazione e con 
la
velocità media dei veicoli che si trovano nella stessa corsia di quello n-esimo e
ad una certa distanza da esso, ottenendo:
(1.13)
Se la corsia adiacente è
di altro tipo, si indica con 
la
differenza massima di velocità tra il veicolo n-esimo e
i veicoli nell’altra corsia, ottenendo:
(1.14)
ed infine, per assicurare
che la differenza di velocità tra due corsie adiacenti sia sempre minore di o
di ,
si scrive:
(1.15)
La terza modifica riguarda l’influenza della salita e della discesa sui parametri caratteristici dei veicoli, in particolare su a(n) e d(n), rispettivamente la massima accelerazione e decelerazione del veicolo n-esimo.
La relazione empirica, di seguito proposta, è utile per tenere in considerazione questo effetto:
(1.16)
Dove “ 
” rappresenta
la pendenza percentuale della strada.
Per utilizzare il modello di Gipps realmente, è necessario separare i veicoli in classi, raggruppandoli in base alle loro prestazioni (a(n),d(n)). Questa elevata approssimazione dei casi di traffico riscontrabili riduce notevolmente la complessità del modello, anche se esso richiede dati molto dettagliati su ogni veicolo, come d'altronde tutti i modelli microscopici. Per tale ragione, il modello di Gipps viene usato o con dati autogenerati o con veicoli dotati di G.P.S. di cui si conosce la posizione e la velocità in ogni istante[9].
1.3.1.2 Cellular Automata
Gli Automi Cellulari (AC) furono ideati nel 1948 da John Von Neumann con la collaborazione del matematico polacco Stanislav Ulam, allo scopo di studiare il comportamento dei sistemi biologici. Poichè Von Neumann era interessato ai principi logici che permettono a un sistema di auto riprodursi e non agli aspetti genetici o fisico-chimici del processo, si concentrò sulle modalità di interazione fra entità elementari, che chiamò automi, per la semplicità del loro comportamento individuale, e cellulari, perché si auto riproducevano come vere e proprie cellule viventi. Successivamente, queste nuove entità vennero studiate e classificate in quattro principali tipologie (a seconda della loro tipica evoluzione verso forme stabili o caotiche) dal fisico e matematico Stephen Wolfram [10].
In generale un automa cellulare è un sistema complesso, composto da un numero finito di unità che interagiscono tra loro. Esso è formato da una griglia di celle, ognuna delle quali cambia di stato, ad intervalli regolari, secondo un insieme di regole che non riguardano soltanto la singola cella, ma anche quelle limitrofe. Gli elementi descrittivi del comportamento di un automa cellulare sono per
ogni cellula:
- lo spazio, che consiste in un reticolo discreto di celle;
- lo stato, in cui essa si trova ad ogni istante discreto di tempo;
- il vicinato, che è l’insieme delle celle ad essa vicine;
- la dinamica, che descrive l’evoluzione di stato in funzione dello stato attuale della cella in considerazione e di quello delle celle vicine;
- i passi temporali discreti di evoluzione.
Oltre agli elementi descrittivi sopra esposti, è possibile dare una definizione formale degli automi cellulari riferendoci a cinque caratteristiche fondamentali:
- l’uniformità: le regole di evoluzione sono le stesse per tutte le celle;
- la località: ogni entità cambia stato tenendo conto solamente di quanto accade entro una certa distanza;
- la sincronicità: a ogni passo temporale le regole sono applicate simultaneamente a tutte le celle;
- l’essere discreto: lo spazio, il tempo e gli stati delle celle sono discreti e non continui;
- l’essere finito: i possibili valori degli stati di una cella sono finiti e non infiniti.
La definizione suppone di essere in uno spazio euclideo, nel quale vengono fissati la dimensione dell’ambiente e il numero degli stati; quest’ultimi in numero almeno pari a due, per evitare il verificarsi di situazioni troppo semplici e banali.
All’interno di questo reticolo si inseriscono le entità (chiamate di solito cellule), che potranno assumere un insieme finito di stati (vivo o morto, un colore, una forma ecc.). Dopo un tempo prefissato tutte le entità cambieranno stato contemporaneamente; il nuovo stato dipenderà dallo stato precedente della singola entità e dagli stati delle entità del vicinato.
Un’altra grandezza da decidere è la distanza massima delle entità da considerare per il cambiamento di stato; questa variabile serve per capire quali celle vicine sono controllate da quella in esame al fine del loro aggiornamento e quindi della loro evoluzione.
L’ultima grandezza da fissare è una funzione di cambiamento di stato. In base a quanto detto, si può definire l’automa cellulare come una quadrupla <d,Q,N,f> in cui:
• d è la dimensione, rappresentata con un numero intero positivo,
• Q è lo spazio degli stati, definito come un insieme finito,
• N è l’indice di vicinato, è un sottoinsieme finito di Zd,
• f è
una funzione definita su 
tale
che, detto 
lo
stato dell’entità nel punto i-esimo dello spazio
Zd al
tempo t,
e indicati con 
gli
elementi di N, risulta:
(1.17)
in ogni punto i ed ad ogni istante t.
L’automa cellulare più
semplice, ma non banale, è quello unidimensionale, avente due soli stati
possibili per ogni cella e con le celle vicine definite come le celle adiacenti
da entrambi i lati. Ogni cella, con le sue due celle vicine, cioè adiacenti, costituisce
un vicinato di tre celle e per questo motivo ci saranno 
possibili
configurazioni di vicinato. Questo porta ad un totale di 
regole
che si possono attuare. L’insieme di questi 256 automi cellulari, generalmente,
sono riportati utilizzando la notazione di Wolfram; il nome dell’automa
cellulare è il numero decimale che in notazione binaria ci fornisce la tabella
delle regole, con elencati gli otto possibili vicinati. Per esempio nella Figura
1.4 è riportata la tabella che definisce il Cellular Automaton 184, CA184.
In numero binario il numero 184 si scrive come 10111000 e quindi la tabella
dell’evoluzione diventa:
Figura 1.4: Regola 184
Nel diagramma i valori possibili delle tre celle componenti in vicinato sono mostrati nella riga di sopra e il valore risultante che assumerà la cella centrale nella generazione successiva è mostrato nella riga sottostante; se è presente un 1 la cella verrà occupata altrimenti resta libera. Quindi inizialmente bisogna scrivere il numero relativo all’automa in notazione binaria; successivamente si dovranno raffigurare gli otto possibili vicinati (riga superiore) e poi a seconda che ci sia un 1 o uno 0 riempire la cella centrale. La rappresentazione grafica dell’evoluzione dopo 12 passi, partendo da una griglia con due sola cella nere (colorate in rosso nella figura per distinguerle dalle altre), è rappresentata in Figura 1.5. La regola 184 può essere usata come un semplice modello per il flusso di traffico ad un’unica corsia e fornisce le basi per molti modelli cellular automata destinati appunto a questo scopo.
In questi modelli le particelle, che rappresentano i veicoli, si muovono in un’unica direzione, si fermano e ripartono in base alle automobili che hanno di fronte a loro. Il numero di particelle rimane invariato durante la simulazione.
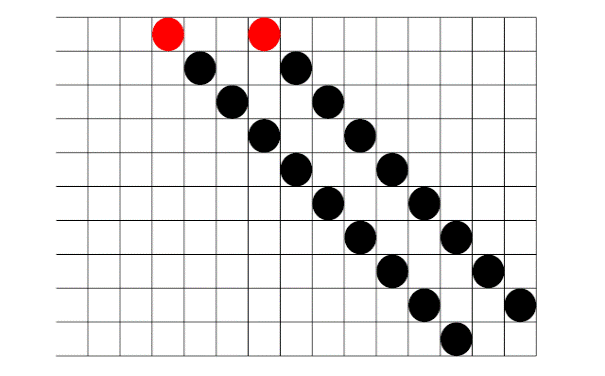
Figura 1.5: Evoluzione della griglia utilizzando la regola 184
Il modello Cellular Automation è uno dei più semplici modelli per la simulazione microscopica. Il modello base è a singola corsia ma può essere facilmente esteso al caso di multi-corsia ed è discreto sia nel tempo che nello spazio. La strada è suddivisa in celle di lunghezza costante ed, in ogni momento, la cella può essere vuota o occupata da un veicolo.
Imponiamo che un veicolo occupi una e una sola
cella e che la sua velocità possa assumere solo valori interi compresi tra 0 e 
.
Ad ogni step lo stato del
sistema è aggiornato seguendo un ben preciso ordine di azioni; l’efficienza
computazionale dei modelli CA è il principale vantaggio di questo sistema
rispetto ad altri. Se si denotano la posizione e la velocità dell’n-esimo
veicolo rispettivamente con 
e 
,
e si chiama 
il
gap tra il veicolo n-esimo e quello che precede, l’aggiornamento allo
step t+1
viene effettuato parallelamente sugli N veicoli
in accordo con le quattro regole seguenti:
1. accelerazione:
se la velocità v di
un veicolo è minore della e
se il gap 
è
maggiore di v+1, allora la velocità viene aumentata
a v
+
1
;
2. rallentamento
(dovuto ad altri veicoli): se il gap del
veicolo n-esimo è
minore della propria velocità, la velocità del veicolo n-esimo viene
ridotta di −1
;
3. randomization: la velocità di ogni veicolo (se maggiore di 0) viene diminuita di 1, con una probabilità p
;
4. movimento: ogni veicolo viene avanzato di v celle
Attraverso i quattro step, le proprietà del traffico sono modellate sulla base delle regole del Cellular automaton; già questo modello semplice mostra un comportamento del sistema non banale e realistico. Lo schema dell’aggiornamento del modello NaSch (dai nomi Nagel e Schreckenberg)[11] è illustrato tramite un esempio in Figura 1.6.
La prima riga rappresenta
la configurazione iniziale; ogni macchina possiede una velocità compresa tra 0
e =
2, indicata dal numero in alto a destra.
Nel primo step, ogni
veicolo aumenta la propria velocità di 1, nel caso in cui quest’ultima sia minore
di .
Nel secondo step, il veicolo che non avrà abbastanza celle vuote dinanzi a sé, ridurrà la propria velocità; per questo motivo la macchina A, dal momento che ha una sola cella libera davanti a sé, riduce la propria velocità di 1. La macchina C riduce la velocità di 2, perché non ha nessuna cella libera.
Nel terzo step, dato che
si è assunto 
,
mediamente
una macchina su tre verrà rallentata; nell’esempio, è accaduto alla macchina A.
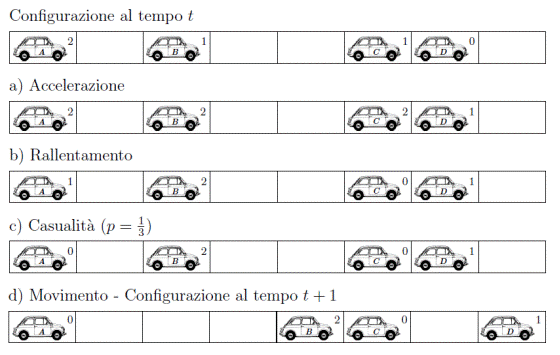
Figura 1.6: Esempio dell’applicazione delle regole di aggiornamento
Nell’ultimo step, si vede la configurazione finale: la macchina A, avendo velocità pari a 0, rimarrà ferma; la macchina B, avendo velocità pari a 2, si sposterà di due celle; la macchina C, avendo velocità pari a 0 non si muoverà; e la macchina D, avendo velocità pari a 1 si sposterà di una cella. Ognuno dei quattro passi ha un obiettivo preciso e prende in considerazione i diversi comportamenti dei veicoli. Il primo passo riflette la tendenza generale dei guidatori a guidare con una velocità il più possibile elevata se ve ne è l’opportunità, senza oltrepassare i limiti consentiti. Il secondo passo è necessario al fine di evitare collisioni e quindi incidenti tra i veicoli. Il passo 3 è essenziale nella simulazione del flusso realistico di traffico poiché, se non ci fosse, la dinamica dei veicoli risulterebbe completamente deterministica; l’inserimento di questa stocasticità considera le variazioni naturali di velocità dovute al comportamento umano e alle circostanze esterne. Questo step, infatti, contempla il differente comportamento dei guidatori, specialmente riguardo ad un’accelerazione non deterministica o ad una reazione eccessiva durante il rallentamento. Ciò è importante per una formazione spontanea del traffico. Senza questa casualità, ogni configurazione iniziale dei veicoli raggiungerebbe molto rapidamente un modello stazionario. Apportare un cambiamento all’ordine degli steps, relativi all’aggiornamento del sistema, potrebbe implicare il cambiamento delle proprietà del modello; se, per esempio, venissero invertiti i passi 2 e 3 non ci sarebbe una reazione alla frenata e pertanto non si avrebbe una spontanea formazione del traffico. Il modello NaSch può essere considerato come un modello cellular automata stocastico. Nel caso di vmax = 1, si ha un’equivalenza del modello con la regola 184 della notazione di Wolfram vista precedentemente, in Figura 1.4. Il modello NaSch, così come altri modelli di traffico, sono stati formulati in modo che non siano possibili incidenti tra i veicoli; tuttavia sappiamo che in condizioni reali, se le condizioni di sicurezza diminuiscono, è possibile la collisione dei veicoli. Per questo motivo, Boccara et Al.[12], hanno modificato la regola di aggiornamento del modello NaSch con la regola:
(1.18)
dove 
è
una variabile random bernoulliana che assume valore 1 con probabilità 
e
0 con probabilità 
.
Un’altra possibile generalizzazione del modello NaSch consiste nel modificare il secondo passo con la seguente regola di aggiornamento:
(1.19)
dove 
è
l’accelerazione assegnata al veicolo n-esimo.
Una limitazione dei modelli car following consiste nel fatto che, in generale, vengano usati per modellare strade ad un’unica corsia. Per quanto riguarda, perciò, la modellizzazione di tratte stradali più grandi, sarà necessario considerare la possibilità di effettuare dei cambi di corsia. A tal proposito i modelli car following vengono migliorati con l’aggiunta di una nuova componente modellistica chiamata lane changing models. Il primo modello lane changing è stato introdotto da Gipps nel 1986[13]; esso passa in rassegna un’ampia casistica riguardante le scelte intraprese dai guidatori in ambito urbano dove i segnali, le ostruzioni e la presenza di veicoli pesanti fanno si che il cambio di corsia diventi un’operazione assai frequente. I tre fattori principali che sono stati valutati nel processo di decisione sono: la necessità, l’opportunità e la sicurezza di un cambiamento di corsia.
La necessità o l’opportunità di modificare corsia è determinata calcolando, per ogni guidatore, un fattore di rischio, il quale è funzione della posizione relativa del veicolo rispetto all’oggetto che dà luogo alla necessità di un cambiamento di corsia. Il fattore di rischio è funzione della decelerazione che un guidatore dovrà applicare se il suo predecessore frena. I fattori di rischio del veicolo in esame nei riguardi di quello che precede e, del veicolo che segue nei riguardi di quello in esame, sono calcolati per ogni cambio di corsia. Il rischio viene poi confrontato con un fattore di rischio accettabile, il quale dipende dal cambiamento di corsia effettuato e dalla sua urgenza. Molti microsimulatori basano i comportamenti lane changing sul modello di Gipps.
A differenza di Gipps (1986), Yang e Koutsopoulos [14], hanno sviluppato un modello lane changing applicabile solo alle autostrade, utilizzando un quadro probabilistico capace di simulare il comportamento del guidatore qualora possa intraprendere più decisioni. In questo modello i cambiamenti di corsia sono classificati come:
- MLC (scelta obbligata), quando il guidatore è obbligato a cambiare corsia, è questo il caso di rampe di uscita,
- DLC (scelta a discrezione), quando il guidatore ritiene che le condizioni di guida nell’altra corsia soddisfano maggiormente le sue necessità.
Un guidatore considera un possibile cambiamento di corsia quando la velocità del veicolo che lo precede è inferiore alla velocità da lui desiderata; in tal caso controlla se sulla corsia adiacente vi è l’opportunità di aumentare la velocità di viaggio. Al fine di valutare se la velocità attuale è sufficientemente bassa e se la velocità nell’altra corsia è sufficientemente elevata, sono stati proposti due parametri: un fattore di intolleranza e un fattore di velocità.
Yang e Koutsopoulos, inoltre, hanno sviluppato un modello gap acceptance che mette in luce il fatto che il valore di gap critico (cioè il gap minimo) riferito ad una situazione MLC è inferiore a quello appartenente ad una situazione DLC.
Recentemente, Ahmed et Al.[15], hanno sviluppato una struttura per un modello un generale di Lane changing, che esamina il comportamento di cambio corsia sia nella situazione MLC che in quella DLC.
Il lane changing viene quindi modellato come una sequenza di quattro passi:
1) la decisione di considerare un cambiamento di corsia,
2) la scelta della corsia,
3) l’accettazione del gap,
4) l’esecuzione della manovra.
Ahmed ha stimato i parametri del modello solo per un caso particolare: l’entrata in autostrada mediante una rampa. In questo caso, è evidente che i conducenti abbiano già intrapreso la scelta di entrare nella corsia adiacente e pertanto, il processo decisionale continua con l’accettazione del gap e l’esecuzione della manovra di svolta.
Secondo Yang e Koutsopoulos (1996), il gap è accettabile solo quando sia il lead gap che il lag gap sono accettabili.
La Figura 1.7 mostra la definizione di lead e lag gap.
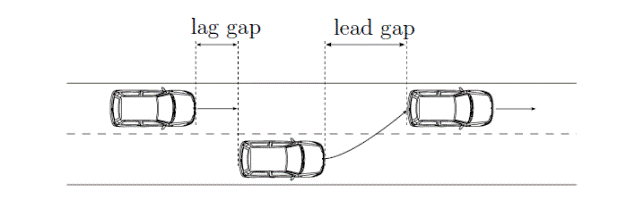
Figura 1.7: Schema della manovra di lane changing
Il lead e il lag gap si
assumono distribuiti secondo una distribuzione lognormale del tipo 
dove
Y
è
distribuita normalmente con media 
e
deviazione standard 
.
La stima del lead gap critico per il guidatore n-esimo
all’istante
t è:
(1.20)
dove:
- 
è il lead critical gap,
-
è
un valore random, costante per ogni guidatore e avente distribuzione normale
- 
varia
al variare del gap e del guidatore; è distribuito secondo N(0,1.612).
La stima del lag gap critico per il guidatore n-esimo all’istante t è:
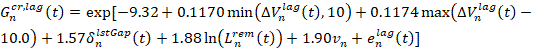(2.16)
dove:
- 
è il lag critical gap,
- 
è la velocità
del veicolo che segue (lag) sottratta a quella del veicolo considerato,
- 
- 
è
il tempo trascorso sotto l’applicazione delle condizioni MLC,
- 
è la
distanza rimanente nella corsia nella quale deve essere completata la manovra
di lane change,
- 
è un valore random distribuito secondo N(0,1.312)
La stima del lane changing, supposto che entrambi i gap siano accettati, è:
(1.21)
In tutti i casi, comunque, il cambio di corsia viene effettuato tenendo in considerazione la corsia attuale, quella prescelta, i possibili veicoli in arrivo già presenti sulla corsia futura, la loro distanza e velocità nonché il grado di propensione al rischio del guidatore. Per questo motivo i modelli di lane changing sono studiati come un caso particolare di gap acceptance.
Il gap acceptance è un elemento importante nella maggior parte dei modelli lane changing. Il conducente stabilisce quando eseguire una manovra (cambiare corsia, attraversare un’intersezione, inserirsi in un flusso di traffico, entrare in una rotatoria, ecc.), valutando se esiste l’intervallo temporale minimo necessario per la manovra, sulla base delle velocità relative degli altri veicoli. I modelli di gap acceptance, pertanto, sono formulati come un problema di scelta binario, nel quale i guidatori decidono se accettare o rifiutare il possibile gap, confrontandolo con un gap critico. Il “Critical gap” è il minimo intervallo di tempo individuato da un veicolo in ingresso prima che esso si immetta nella corrente di traffico. Il “Reject gap”,invece, è l’intervallo di tempo che definisce l’incapacità del veicolo di immettersi in una corsia a causa dell’eccessivo flusso. Per cui avremo come “Maximum reject gap” il più grande tra i “Reject gap” di tutti i veicoli rispetto al singolo veicolo.
Differenti modelli di gap acceptance sono stati sviluppati negli anni Sessanta e Settanta e sono basati sull’ipotesi che il critical gap segua una specifica distribuzione di probabilità.
Herman e Weiss[16], hanno supposto che il gap sia distribuito con una distribuzione esponenziale, Drew et al., in [17], hanno usato una distribuzione lognormale, e Miller, in [18], ha assunto una distribuzione normale. Daganzo, in [19], utilizzò una formulazione appropriata del particolare modello probit (specificazione di un modello di regressione binaria) per stimare il gap acceptance. Il gap critico per il conducente n-esimo all’istante t è espresso dalla seguente relazione:
(2.18)
dove:
-
è una componente del gap critico attribuibile al guidatore n-esimo,
- 
è
un valore random che varia al variare del gap e del guidatore.
Si assume che queste due
variabili siano indipendenti e, inoltre, che sia
distribuita con una distribuzione normale di media G e
varianza 
e
che sia
distribuita con distribuzione normale di media 0 e varianza 
Mahmassani e Sheffi, in [20], hanno utilizzato i dati raccolti da Daganzo (1981), scegliendo come distribuzione del gap critico quella normale. La media di tale distribuzione dei gap è funzione di alcune variabili esplicative, le quali descrivono l’interazione di diversi fattori influenzanti il comportamento dei guidatori riguardo l’accettazione del gap. La variabile numero di gap rigettati, analizzando il fattore di impazienza, ha un riscontro importante per quanto riguarda la condotta del guidatore.
Highway Capacity Manual, in [21], utilizza la media del gap critico a un incrocio per stimare il ritardo e la capacità di quest’ultimo. HCM definisce il gap critico, per un’intersezione controllata da due stop, come la media di tutti i gap accettabili. Una grave limitazione di tale definizione è che un’osservazione su un grande gap accettato da un conducente non fornisce informazioni circa il minimo gap accettabile. Nella revisione della procedura HCM, il gap critico è definito come il più grande gap rigettato. Questa definizione è ancora imperfetta, poiché un guidatore molto prudente può aumentare notevolmente la stima, in quanto, anche con gap elevati non effettua la manovra. In aggiunta, Cassidy et Al., in [22], hanno elencato altre carenze di questo approccio, tuttavia la definizione HCM rimane molto vantaggiosa in quanto consente di stimare molto facilmente il parametro Gap Acceptance.
Kita, in [23], usò un modello logit per stimare il gap nei casi di fusione di una rampa con l’autostrada. Egli, oltre la lunghezza del gap, valutò la velocità relativa del veicolo rispetto a quella della corsia principale, nonché la distanza rimanente sulla corsia d’accelerazione, parametri influenzanti il comportamento del guidatore.
Cassidy et Al. (1995), utilizzando l’approccio di Kita, sono giunti alla conclusione che una funzione con fattori diversi ha più significato di una che include solo la media dei gap.
[1] Rivadossi, M. (2004) Metodologie per la modellazione di un’area critica: Il caso della zona Piazza Arnaldo-Canton Mombello a Brescia, Tesi di laurea, Università degli Studi di Brescia, Facoltà di Ingegneria Civile.
[2] Ortúzar, J. e L.G. Willumsen (1995) Modelling Transport, J. Wiley & Sons, New York, USA.
[3] Cascetta E. (2006) “Modelli per i Sistemi di Trasporto: Teoria e Applicazioni” UTET editore.
[4] Schwarze, B., D. Strauch, H. Mühlhans e G. Rindsfüser (2004) Bedarf, Anforderungen und Verwendung räumlicher Daten in einer integrierten, dynamisch-mikroskopischen Simulation der Stadtentwicklung, In: Raubal M., A. Sliwinski and W. Kuhn, Eds. (2004) Geoinformation und Mobilität - Von der Forschung zur praktischen Anwendung. IfGIprints 22. Verlag Natur & Wissenschaft, Solingen, Germany.
[5] L. A. Pipes, “An operational analysis of traffic dynamics,” Journal of Applied Physics, vol. 24, no. 3, pp. 274–281, 1953, http://link.aip.org/ link/?JAP/24/274/1.
[6] A. Reuschel, “Vehicle movements in a platoon,” Oesterreichisches Ingenieeur-Archir, vol. 4, pp. 193–215, 1950.
[7] R. Chandler, R. Herman, and E. Montroll, “Traffic dynamics: Studies in car following,” Opns. Res., vol. 6, pp. 317–45, 1958.
[8] P. Gipps, “A behavioural car following for computer simulation,” Transp. Res. B15, pp. 105–111, 1981.
[9] “TSS-transport simulation systems,” http://www.tss-bcn.com.
[10] S. Wolfram, A New Kind of Science, 2002.
[11] K. Nagel and M. Shreckenberg, “A cellular automaton model for freeway traffic,” J. Phisique I, vol. 2, no. 12, pp. 2221–2229, 1992.
[12] N. Boccara, H. Fuks, and Q. Zeng, “Car accidents and number of stopped cars due to road blockage on a one-lane highway,” Physical Review A, vol. 30, p. 3329, 1997.
[13] P. G. Gipps, “A model for the structure of lane-changing decisions,” Transportation Research Part B, vol. 5, pp. 403–414, 1986.
[14] Q. Yang and H. Koutsopoulos, “A microscopic traffic simulator for evaluation of dynamic traffic management systems,” Transportation Research Part C: Emerging Technologies, vol. 4, no. 3, pp. 113–129, 1996.
[15] K. Ahmed, E. Moshe, H. Koutsopoulos, and R. Mishalani, “Models of freeway lane changing and gap acceptance behavior,” 1996.
[16] R. Herman and G. H. Weiss, “Comments on the highway crossing problem,” Operations Research, vol. 9, pp. 828–840, 1981.
[17] D. R. Drew, L. R. LaMotte, J. H. Buhr, and J. A. Wattleworth, “Gap acceptance in the freeway merging process,” Highway Research Record. No 208, pp. 1–16, 1967.
[18] A. J. Miller, “Nine estimators of gap acceptance parameters,” Bulletin Transport Section, Civil Engineering, pp. pp. 215–235, 1972.
[19] C. F. Daganzo, “Estimation of gap acceptance parameters within and across the population from direct roadside observation,” Transportation Research Part B 15B, pp. 1–15, 1981.
[20] H. Mahmassani and Y. Sheffi, “Using gap sequences to estimate gap acceptance functions,” Transportation Research Part B 15B, pp. 143–148, 1981.
[21] “HCM - highway capacity manual,” TRB Special Report 209, washington D.C.: Office of Research, FHWA.
[22] M. J. Cassidy, S. M. Madanat, M. Wang, and F. Yang, “Unsignalized intersection capacity and level of service : Revisiting critical gap,” Transportation Research Board, 74th Annual Meeting, 1995.
[23] H. Kita, “Effect of merging lane length on the merging behavior at expressway on ramps,” Transportation and Traffic Theory, pp. 37–51, 1993, in C. F. Daganzo (Ed.).
2.1 Descrizione del software INTEGRATION 2.30
Il modello INTEGRATION fu sviluppato da Michel Van Aerde agli inizi degli anni ottanta presso l’Università di Waterloo, in Canada. Il nome INTEGRATION deriva dal fatto che il modello “integrates”, cioè unisce e racchiude in sé, una serie di potenzialità uniche. In primo luogo, il modello propone l’uso combinato di singoli veicoli e teoria del deflusso microscopico, rappresentando il flusso con una serie di veicoli che rispettano singolarmente alcune relazioni di deflusso macroscopiche, definite per ogni ramo della rete, [1]. Proprio per questa sua caratteristica di modellazione, ovvero sia per singoli veicoli (visione microscopica) sia per un flusso di traffico (visione macroscopica), INTEGRATION risulta assimilabile ad un sistema ibrido e quindi inseribile tra i modelli di tipo mesoscopico. Questa capacità consente di superare il divario tra il campo di applicazione dei modelli di pianificazione della rete e gli strumenti operativi necessari a fornire il miglior livello di soluzione possibile.
In secondo luogo, il modello ha integrato i tradizionali Sistemi di Trasporto Intelligenti quali, ad esempio, ATMS (Advanced Traffic Management Systems) e ATIS (Advanced Traveler Information System).
Nel corso degli anni Integration è evoluto considerevolmente da tali origini mesoscopiche . Questa evoluzione ha avuto luogo grazie alla valorizzazione e alla raffinatezza di alcune nuove funzioni implementate durante il periodo di applicazione pratica del modello. Alcuni di questi miglioramenti decisivi, quali l'aggiunta del car-following, del lane changing, e anche di un assegnazione dinamica del traffico, hanno rafforzato il modello del flusso di traffico. Inoltre, l'inserimento di funzionalità per la modellazione dei caselli e le emissioni dei veicoli hanno avuto un ruolo determinante ed, unite ad altre caratteristiche, quali la grafica in tempo reale, l'animazione e le statistiche dei veicoli sonda, hanno reso il modello più facile da capire, convalidare e calibrare.
INTEGRATION, pertanto, è un modello di simulazione del traffico a livello microscopico in grado di tracciare i singoli movimenti di ogni veicolo della rete dall’origine alla destinazione. L’aggiornamento dello stato del veicolo è eseguito ogni decimo di secondo o deci-secondo, affinché l’utente possa avere un buon grado di conoscenza e comprensione delle caratteristiche della microsimulazione.
Il software è capace di modellare l’insieme di decisioni che l’utente, alla guida di un veicolo, prende per spostarsi da un’origine verso una certa destinazione. Le decisioni intraprese dal conducente possono essere classificate in due grandi tipologie:
- Decisioni di tipo pre-trip:
Ovvero decisioni che l’utente deve prendere prima di iniziare lo spostamento. Si tratta di decisioni, riguardanti la destinazione da raggiungere, il mezzo da utilizzare per effettuare lo spostamento e, inoltre, l’istante temporale in cui iniziare lo spostamento stesso. Ognuna di queste decisioni è indipendente dalle altre, ma solitamente vengono prese contemporaneamente. La decisione rispetto ad un potenziale spostamento deve tener conto anche della possibilità di effettuarlo per un dato istante di partenza . Una volta presa la decisione di fare il viaggio verso una data destinazione, il viaggiatore deve decidere come effettuare lo spostamento, se utilizzare autovetture private o mezzi pubblici, se utilizzare uno o più veicoli.
- Decisioni di tipo on-route:
Ossia decisioni che l’utente prende intanto che lo spostamento è in atto. Questo tipo di decisioni non vengono stabilite in maniera univoca, ma sono intraprese e aggiornate mentre lo spostamento è in atto. Rientra in questa famiglia di decisioni quella della scelta del percorso. Infatti, una volta stabilito l’itinerario, il conducente può decidere di modificarlo, anche in maniera parziale, durante lo spostamento. Altra importante decisone, che il conducente di un veicolo deve effettuare durante il viaggio, riguarda la velocità con cui procedere e la corsia da percorrere. In particolare, prima di iniziare il viaggio, si deve scegliere la rotta da seguire. Questa scelta solitamente non viene fissata all’inizio del viaggio ma si preferisce lasciare al guidatore la libertà di modificarla durante il percorso. Una volta che il veicolo è entrato lungo questo percorso, il conducente deve scegliere anche in base alla propria velocità la corsia da utilizzare (se possibile). La velocità e il cambiamento di corsia si modificano spesso anche lungo un collegamento a causa di interazioni con altri veicoli. Infine, quando il conducente arriva alla fine di un collegamento, può essere costretto ad attraversare un flusso di traffico opposto e deve decidere se accettare o respingere tutti gli eventuali gap e quindi fondersi con il flusso di traffico convergente .
Il campo attuale di applicazione della versione commerciale del modello di Integration include una serie di decisioni prese dal conducente, una volta che il viaggio è iniziato. Questo set di decisioni inizia dal momento in cui il conducente ha deciso di spostarsi da una determinata origine a una particolare destinazione, in un determinato momento, e per mezzo di un’auto privata. Ciò implica che, allo stato attuale, il modello commerciale di INTEGRATION, non contempla l’effetto causato dai guidatori che scelgono di partire in un altro momento, con un mezzo differente, o con una destinazione alternativa. Tuttavia, visto l’interesse crescente in merito all’impatto che queste decisioni possono avere sul traffico, è stata sviluppata una versione che aggiorna il modello di simulazione di INTEGRATION. Questo aggiornamento permette di valutare i cambiamenti delle modalità di viaggio, orario di partenza o destinazione da raggiungere in modo iterativo attraverso le applicazioni del modello (l’aggiornamento non è stato usato nel presente progetto).
2.3 Input e Output del modello
INTEGRATION è un modello microscopico in grado di tracciare, con una precisione di 1/10 di secondo, sia i movimenti laterali che quelli longitudinali dei veicoli. Esso permette di rappresentare la domanda di traffico, la selezione dei percorsi e la capacità dei rami. È possibile, ancora, eseguire il controllo del traffico in modo variabile nel tempo, con continuità, definendo intervalli di tempo comuni, nei quali determinare le suddette caratteristiche. È capace, inoltre, di gestire l’evoluzione dei tassi di partenza dei veicoli da un’origine ad una destinazione, i tempi di semaforizzazione e altri fenomeni del traffico con continuità nel tempo e non come sequenza di stati stazionari. La logica di funzionamento è la seguente: prima di iniziare la simulazione vera e propria, tutti i veicoli devono essere generati e poi caricati sulla rete. Il tutto viene effettuato sulla base dell’indicazione della destinazione da raggiungere, partendo da una certa origine; a tal proposito la domanda complessiva viene scomposta in serie temporali con un certo numero di istogrammi, raffiguranti i tassi di partenza per ogni coppia O/D, appartenente alla rete. Ogni cella dell’istogramma può avere una durata temporale differente, che va da 1 secondo a 24 ore. Quando la stessa coppia O/D viene ripetuta nella lista di partenza, con una sovra saturazione temporale, i veicoli vengono sommati. Ogni veicolo viene identificato in maniera univoca, così come tutti gli spostamenti all’interno della rete. Vengono registrati, inoltre, tutti i dati caratteristici (velocità, accelerazione, tempo di fermata, ecc..) di ciascun veicolo. Quando un veicolo parte dalla sua zona di origine procede di ramo in ramo, selezionando la corsia sulla quale muoversi in base al distanziamento dagli altri veicoli. Selezionata la corsia su cui viaggiare, il veicolo regola la propria velocità in relazione alla distanza intercorrente con il veicolo, che lo precede sulla stessa corsia. Altra importante caratteristica del software è la possibilità di simulare incidenti, avvenuti sulla rete stradale, e analizzare le conseguenze che questi determinano a livello di traffico veicolare. Gli incidenti possono avere una qualunque durata e possono avvenire in un qualsiasi punto della rete. La gravità di un incidente può essere simulata sulla base della riduzione di capacità del tratto stradale interessato e può variare da un minimo pari a 0% a un massimo pari al 100%. È possibile, inoltre, simulare la presenza contemporanea di più incidenti su uno stesso tratto stradale. La presenza di un incidente su un tratto di strada determina una riduzione della massima velocità a cui i veicoli possono procedere, tutto ciò può far si che per alcuni veicoli della rete sia più conveniente scegliere strade alternative per raggiungere la meta prefissata. Per poter effettuare una simulazione in INTEGRATION è necessario creare alcuni file di input forniti come file di testo o sotto forma di tabelle. I file richiesti dal programma sono:
- Master Control File (file di settaggio)
- File 1: contiene le coordinate, le caratteristiche e gli attributi dei nodi della rete.
- File 2: contiene le strutture, le caratteristiche e le coordinate degli archi della rete.
- File 3: contiene la descrizione dei piani di semaforizzazione da inserire nella rete.
- File 4: contiene la descrizione della domanda di spostamento da un’origine ad una destinazione
- File 5: contiene la descrizione degli incidenti presenti sulla rete.
Per il corretto funzionamento del programma occorre fornire in input tutti i dati necessari per la modellazione del sistema; essi vengono inseriti in INTEGRATION tramite un file di settaggio (master control file) che li elabora e li restituisce nei file output, [2].
Il master control file, file di testo con estensione .INT, deve contenere informazioni su nomi e directory di appartenenza dei file di input e di output e, specificare la durata dell’intera simulazione e l’intervallo di tempo di generazione degli output. In parole più semplici il master control file gestisce i tempi di simulazione, indica ad INTEGRATION da quale cartella prelevare i file di input e in quale cartella generare gli output.
La struttura di tutti i file di input è sostanzialmente quella di una tabella, caratterizzata dalle presenze di righe e colonne. Ogni riga (escluse le prime) rappresenta una componente dei file ed ogni colonna ne descrive le caratteristiche specifiche. La struttura delle righe è uguale per quasi tutti i file ma le colonne avranno di volta in colta un numero ed un significato diverso. Bisogna precisare che l’implementazione dei file di input è la maggiore difficoltà legata all’uso del programma, non solo per la complicata comprensione delle righe di testo, ma anche per il dispendio di tempo. Tuttavia si ricorda, che in fase di simulazione, il programma riesce ad individuare gli errori e indica il file di input dove è stato commesso.
Una volta terminata la simulazione, il programma fornisce degli output che è possibile distinguere principalmente in due differenti tipologie:
- Output grafico: è rappresentato da un’interfaccia grafica, che visualizza in maniera istantanea ed intuitiva l’evolversi del traffico sulla rete stessa.
- Output di testo: è costituito da files di testo che forniscono un’analisi più dettagliata di tutti i fenomeni che si verificano sulla rete in esame.
Gli output grafici di INTEGRATION sono costituiti da rappresentazioni animate dal traffico, nelle quali viene visualizzata l’intera rete modellizzata, nonché tutti i veicoli in movimento sui suoi tronchi stradali (vedere Figura 2.1). Tramite gli output di testo, invece, è offerta all’utente la possibilità di ottenere stime dei tempi di percorrenza sugli archi, delle lunghezze medie delle code, dei consumi di carburante, delle emissioni di inquinanti, oltre che statistiche aggregate per arco e per coppia origine destinazione.
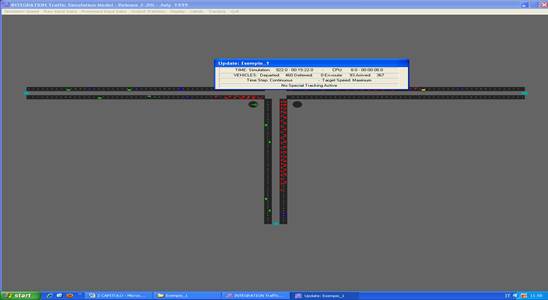
Figura 2.1: Output grafico di INTEGRATION
2.4 Approccio al modello microscopico
Questo approccio microscopico consente l'analisi di molti fenomeni dinamici di traffico, quali le ondate veicolari, il gap acceptance, il divario tra i veicoli; cioè molti aspetti che sarebbero di difficile valutazione se operassimo in condizioni non- stazionarie utilizzando un tipo di modello macroscopico basato sulla rete. Per esempio, in una rete dinamica, il dato medio del gap acceptance, generalmente, non può essere utilizzato per le svolte a sinistra se la percentuale del flusso opposto varia da ciclo a ciclo o all'interno di un particolare ciclo. L’approccio microscopico di INTEGRATION è da ritenersi un mezzo per raggiungere un fine, piuttosto che un fine in sé. Questa scelta non aumenta significativamente i requisiti di memoria e di calcolo del modello, ma è finalizzata a un miglioramento del grado di fedeltà con cui è possibile rappresentare le condizioni dinamiche del traffico. Il modello di INTEGRATION non si limita a fissare gli istanti di partenza, i segnali orari, la gravità degli incidenti o i percorsi di traffico ma è in grado di trattare ciascuno dei suddetti attributi del modello, non come una sequenza di stati costanti, ma come parametri modificabili nel corso del tempo, in [3].
L’approccio microscopico consente, inoltre, una notevole flessibilità qualora si vogliano rappresentare variazioni spaziali nelle condizioni del traffico.
Ad esempio, mentre la maggior parte dei modelli assume le condizioni del traffico il più possibile uniformi, lungo un dato collegamento, INTEGRATION permette, invece, una variazione continua della densità del traffico su tutta la lunghezza del collegamento. In particolare, una simile variazione dinamica di densità su un’arteria, permette la rappresentazione della partenza di plotoni di veicoli da un semaforo e la conseguente propagazione di onde di shock verso monte e/o verso valle. In conclusione, è importante notare che, sebbene il modello sia soprattutto microscopico, queste regole microscopiche sono state attentamente calibrate al fine di catturare la maggior parte delle caratteristiche macroscopiche del traffico che sono più familiari agli ingegneri trasportisti. Alcune di queste caratteristiche sono le relazioni di velocità-flusso nei collegamenti, l’assegnazione del traffico, il ritardo casuale e quello dovuto alla sovra saturazione. La sfida principale nella progettazione di INTEGRATION è quindi stata quella di garantire che queste importanti caratteristiche macroscopiche si distinguessero dalle regole fondamentali del modello microscopico, necessarie per rappresentare le dinamiche del sistema usando un unico approccio integrato, in [4].
Il modo in cui INTEGRATION rappresenta i flussi di traffico, può essere meglio spiegato disquisendo in merito a come un veicolo tipo inizia il suo viaggio, seleziona la sua velocità, effettua il cambio di corsia, si sposta di arco in arco, e sceglie il suo percorso.
Prima di iniziare la simulazione, occorre generare i singoli veicoli che devono essere caricati sulla rete. Poiché la maggior parte delle matrici O/D presentano informazioni di natura macroscopica, INTEGRATION consente di specificare la domanda di traffico come una serie temporale di matrici O/D per ogni possibile coppia O/D presente all'interno della rete.
Ogni cella istogramma all'interno di questa serie temporale può variare in durata da 1 secondo a 24 ore e, la durata di ciascuna cella è indipendente dalla matrice O/D successiva o dal successivo intervallo di tempo.
La generazione dei singoli veicoli avviene in modo tale da soddisfare gli indici macroscopici di variazione temporale delle partenze, i quali sono forniti al modello attraverso i file di input, come illustrato nella Figura 2.2. Si può notare che il modello, prima che inizi la simulazione, in uno specificato intervallo di tempo variabile, scompone la domanda della matrice O/D in una serie di singoli veicoli. Ad esempio, se il dato O/D aggregato di input richiede partenze con un passo uniforme di 600 veicoli / ora tra le 8:00 e le 8:15 AM, allora saranno generati un totale di 150 veicoli con un intervallo di 6 secondi l’uno dall’altro. Si deve notare che, come precedentemente specificato, il file della domanda è disaggregato; ciascuna delle partenze dei singoli veicoli è contrassegnata con l’istante di partenza desiderato, con l’origine e la destinazione del viaggio e con un numero identificativo relativo al veicolo stesso. Questo numero può essere utilizzato per rintracciare il veicolo mentre procede verso la sua destinazione.
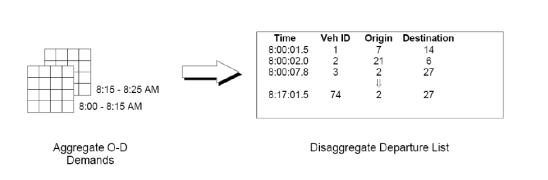
Figura 2.2: Conversion of aggregate O-D traffic demands into disaggregate departure list
2.5.1 Valutazione della velocità veicolare
Quando l’istante della simulazione ha raggiunto il tempo di partenza di uno specifico veicolo, quest’ultimo entra nella rete dalla zona di origine . Da questo punto in poi il veicolo procede verso la destinazione finale, passando di arco in arco. Una volta entrato nel primo tratto, il veicolo seleziona la corsia di marcia. Questa è di solito la corsia con la massima distanza disponibile per il movimento del veicolo. Una volta scelta la corsia, il veicolo calcola la sua velocità desiderata in base al distanziamento esistente tra esso e il veicolo immediatamente a valle che marcia nella sua stessa corsia. Questo calcolo si basa su una specifica relazione del modello microscopico di car following, opportunamente calibrata al fine di ottenere dato aggregato flusso-velocità conforme al particolare collegamento [1]. Nota la velocità del veicolo, è possibile adeguare la posizione dello stesso in base alla distanza percorsa a quella velocità in un deci-secondo. Sulla base di queste posizioni aggiornate, rilevate dopo ogni decimo di secondo, verranno calcolate le nuove velocità ed i nuovi intervalli, relativi ai deci-secondi successivi. La calibrazione macroscopica della relazione microscopica di car following, assicura che i veicoli si spostino coerentemente al legame esistente tra la velocità desiderata e quella libera (free speed), alla velocità alla capacità e alla densità massima. La Figura 2.3 illustra la corrispondenza diretta tra aspetti macroscopici, quali velocità del flusso, e la relazione velocità-densità. Questa corrispondenza è illustrata per tre diverse condizioni di traffico, che sono identificate con i punti a, b, c. A partire dal rapporto velocità-flusso, è possibile rilevare che, il punto a rappresenta condizioni non congestionate , mentre b rappresenta la capacità massima del flusso e c è invece relativo a condizioni congestionate. In sostanza si può affermare che i veicoli sono in grado di mantenere la velocità desiderata quanto più il distanziamento tra essi risulti importante, viceversa questa velocità è destinata a ridursi man mano che aumenta la densità veicolare, e quindi, con la conseguente riduzione del distanziamento tra i veicoli.
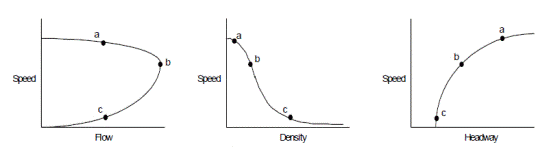
Figura 2.3: Determination of microscopic speed from corresponding macroscopic relationships.
Una conseguenza naturale della logica del car following seguita da INTEGRATION, è quella di rappresentare tutte le code come orizzontali piuttosto che come entità verticali. Una tale rappresentazione assicura che le code si rovescino correttamente all’indietro lungo l’arco, cioè verso monte, nello spazio e nel tempo (fenomeno di spill-back). Inoltre, l'uso del rapporto speed-headway, consente di considerare variabile la densità della coda, in funzione delle velocità associate ai veicoli che costituiscono la coda stessa.
Altra componente principale nel modello di INTEGRATION è la funzione di lane changing. I cambi di corsia possono essere obbligatori o discrezionali, Figura 2.4. La discrezionalità si realizza quando vi è l’opportunità di ottenere un vantaggio, ad esempio, quando vi è la possibilità, cambiando corsia, di aumentare la velocità di marcia. I cambi di corsia però richiedono un gap abbastanza grande per eseguire la manovra. Pertanto, se la manovra non presenta vantaggi, l’auto rimarrà nella sua corsia e continuerà il viaggio, oppure, qualora la manovra risultasse conveniente ma non ci fosse abbastanza spazio per effettuarla, il veicolo rallenterà aspettando un gap che permetta il cambio di corsia.
Il cambio discrezionale è funzione delle condizioni prevalenti di traffico, mentre i cambi di corsia obbligatori sono di solito funzione della geometria della rete.
Al fine di determinare se è opportuno effettuare un cambio di corsia (discrezionale), ogni veicolo calcola tre velocità alternative ogni decimo di secondo. La prima alternativa rappresenta la velocità potenziale alla quale il veicolo può continuare a viaggiare nella corsia in cui si trova, mentre la seconda e la terza alternativa rappresentano la velocità potenziale alla quale il veicolo può viaggiare nella corsia posta immediatamente alla sua sinistra e immediatamente alla sua destra. Il veicolo pertanto sceglierà di viaggiare nella corsia che gli consentirà di raggiungere la massima tra queste tre velocità. Ad esempio nella Figura 2.4, il veicolo D sceglie di lasciare la propria corsia per quella di centro al fine di aumentare il distanziamento e quindi la velocità. Non dimentichiamo comunque che, in base a quanto detto prima, il cambiamento di corsia (discrezionale) è anche funzione del gap tra i veicoli. Mentre i cambi discrezionali di corsia sono effettuati da un veicolo al fine di ottimizzare la sua velocità, i cambi di corsia obbligatori derivano principalmente dalla necessità del veicolo di seguire la connessione della corsia alla fine di ogni collegamento. Ad esempio, sempre dalla Figura 2.4, si evince che il veicolo M avrebbe il desiderio di rimanere nella corsia mediana, al fine di mantenere una velocità elevata, tuttavia è costretto a rallentare ed a entrare nella corsia di decelerazione per accedere alla rampa di uscita.
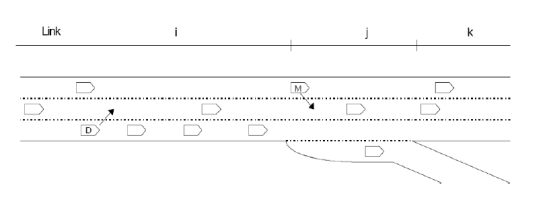
Figura 2.4: Discretionary and mandatory lane changes
La rete stradale in INTEGRATION è fatta come un insieme di connessioni, che consentono il transito di un flusso di traffico in una direzione, su una o più corsie. Alla fine di ogni collegamento, il veicolo entrerà nel successivo, fino a quando non raggiungerà la sua destinazione finale. I collegamenti possono presentare alcune limitazioni. Il software consente di definire anche le corsie riservate ad alcuni tipi di veicoli (bus, taxi, etc...). Inoltre, le manovre di svolta possono essere limitate, cioè effettuabili solo in specifiche corsie, o anche impedite dalla geometria della strada. Per quanto riguarda il routing, in INTEGRATION gli spostamenti origine-destinazione sono eseguiti sulla base di alcune informazioni. Il percorso intrapreso dai veicoli è caratterizzato da un punto d’inizio (origine), un punto di fine (destinazione) e da una tabella di spostamenti. I percorsi indicati nella tabella possono essere statici e deterministici, cioè risultano predeterminati (ad esempio inseriti dal modellatore o automaticamente, utilizzando l’algoritmo di Dijkstra), oppure possono essere dinamici e stocastici, cioè determinati sulla base del livello di congestione interessante il tratto stradale. INTEGRATION consente la coesistenza di diverse tabelle di routing, ciò facilita, ad esempio, l’assegnazione di traffico multi-path.
2.5.4 Selezione della Rotta e assegnazione del traffico
La scelta del prossimo collegamento da percorrere è legata alla logica interna del modello di routing, in [5]. Esistono diverse variazioni al modello base dell’assegnazione, di conseguenza, i dettagli di questa vanno al di là del campo di applicazione della simulazione creata. In generale, esistono all'interno del modello tantissimi modi, tutti diversi, per individuare il collegamento a valle. Comunque, indipendentemente dalla tecnica che viene utilizzata per determinare le rotte, quest’ultime vengono trasmesse al veicolo simulato utilizzando una tabella in formato look-up, vedi Figura 2.5. Questo routing nella tabella di look-up, indica il prossimo link da prendere per raggiungere una destinazione particolare. Al termine di ogni link, un veicolo della pertinente tabella di look-up, sarà legato all’attuale collegamento da attraversare. Ciò consente al veicolo di determinare il percorso da seguire per raggiungere la destinazione finale nella maniera più efficiente. Raggiunto e completato il nuovo collegamento, il processo viene ripetuto, e così per ogni collegamento fino a quando non sono stati attraversati tutti i link che portano alla destinazione finale. Al fine di assegnare un traffico multi-path, sarà necessario inserire un set di più tabelle indicanti il relativo percorso di routing. La simulazione osservata all'interno di questo processo di assegnazione di traffico ha fatto riscontrare che i movimenti di svolta e quindi tutti i cambi di corsia obbligatori, sono basati sul percorso di uno specifico veicolo, piuttosto che su percentuali di svolta arbitrarie.
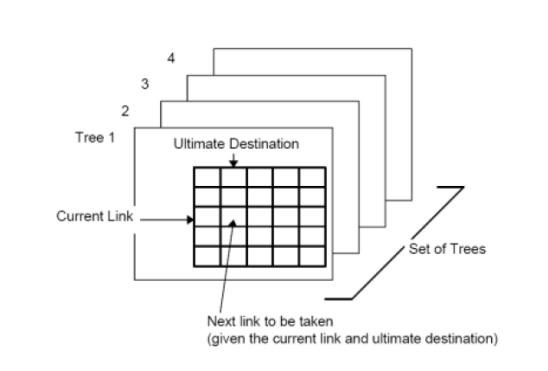
Figura 2.5: Illustration of the routing tree table concept
2.5.5 Modello di Gap Acceptance e segnali di traffico
Uno dei compiti più complessi del modello, nella stima della capacità sia dei segnali stradali isolati che coordinati, è il trattamento delle svolte a sinistra permissive e/o a destra quando è acceso il rosso. In ambiente INTEGRATION, un modello microscopico di Gap Acceptance è utilizzato per riflettere l’effetto causato dai flussi avversari su l'una o l'altra di queste opposte manovre, in [6]. Questa opposizione è misurata automaticamente dal modello, in ciascuna intersezione, mediante l’utilizzo di una logica che specifica quali movimenti contrari entrano in conflitto per ciascuna manovra effettuata sul collegamento oggetto di analisi. Questa logica interna inoltre individua i movimenti di svolta che si oppongono all'interno di una stessa corsia o di uno stesso arco. Tutto ciò permette di valutare l'impatto delle manovre permissive verso sinistra e la durata delle fasi di svolta a sinistra in modo molto dettagliato.
2.6 Emissioni veicolari di HC, CO e NOx
Una serie di modelli compatibili con le emissioni dei veicoli sono accoppiati al modello di consumo di carburante. Questi modelli, che stimano gli idrocarburi, il monossido di carbonio e le emissioni di protossido di azoto, sono sensibili alla velocità del veicolo e alla temperatura ambientale. Tali modelli hanno dimostrato che l’emissione di questi tre composti inquinanti è spesso legata al veicolo, al tempo di viaggio, alla distanza, alla velocità e al consumo di carburante in modo non lineare. Di conseguenza, la gestione strategica del traffico, che può avere un impatto positivo su un provvedimento, non sempre garantisce un effetto positivo su una qualsiasi di queste tre misure. Pertanto, le analisi da effettuare, devono essere estese ben oltre il limite del modello EPAs MOBILE5, che considera un unico profilo di velocità e considera il numero di miglia percorso dal veicolo la principale variabile di previsione, in [7], [8].
2.7 Aggregazione delle statistiche sui link e coppie O/D
Il concetto di time card, utilizzato per rilevare i tempi di viaggio del veicolo e il numero delle fermate su un particolare collegamento, è anche utilizzato per monitorare il consumo di carburante e le emissioni cumulative di ciascun veicolo su ogni link. Inoltre, queste statistiche vengono ulteriormente aggregate per tutti i link attraversati da un determinato veicolo e per tutti i veicoli che hanno attraversato un particolare tratto di strada. I dati statistici possono essere aggregati a livello di matrice O/D, riferite a un certo intervallo di tempo o alla tipologia di veicolo, oppure si possono presentare aggregati per differenti periodi di tempo, mediante l’uso di una griglia fatta di celle aventi latitudine e longitudine. Quando i dati sulle emissioni sono monitorati da latitudine e longitudine in una serie temporale, questi possono servire, a loro volta, come input per un altro modello sulle qualità delle emissioni atmosferiche, relativamente all'intera area urbana. Oltre a rilevare il numero di cambi di corsia che si verificano all'interno della rete, contando il numero di lascia passare per i veicoli, il modello fornisce anche una stima del rischio di incidenti.
Il modello impiegato in INTEGRATION consente di ottenere un livello di rappresentazione più realistico mediante l’impiego di detector loop o di veicoli sonda posti lungo il tracciato. In particolare, quando un veicolo attraversa un anello rivelatore, il modello registra il passaggio del veicolo, la velocità e stima anche il tasso di occupazione. Questi dati sono poi cumulati in un intervallo di tempo, ad esempio di 20, 30 o 60 secondi , che può essere fornito come ulteriore modello di produzione. La capacità di individuare il passaggio di un veicolo su ciascun collegamento oppure di più veicoli su tutta la rete, consente di ottenere un maggior numero di statistiche. Inoltre, ciò permette il monitoraggio in tempo reale di possibili incidenti. Qualora il veicolo fosse contrassegnato come veicolo sonda, il software genera un registro separato all’inizio o alla fine del viaggio del veicolo stesso. Un registro separato può essere generato anche ogni qual volta un veicolo sonda completa un link, oppure per intervalli di tempo regolari, ad esempio ogni secondo. Queste ultime statistiche, più dettagliate, sono utili per il monitoraggio del profilo di velocità dei veicoli che si muovono lungo un arco.
2.9 Transizione Link-to-Link corsia
Quando il veicolo si appresta a raggiungere la fine di un link esso si sposta automaticamente lungo la corsia che gli consente di accedere al collegamento successivo posto a valle. Questa condizione di transizione o spostamento, in realtà, è influenzata dal fatto che deve sussistere un’adeguata distanza di sicurezza, quindi un valore soddisfacente della densità del traffico. Se ciò non accadesse, il veicolo manterrebbe la sua posizione originale finché non si presentasse l’occasione per eseguire lo spostamento. Questa situazione si delinea nel momento in cui si verificano delle code a valle del collegamento, le quali poi si propagano all’indietro, risalendo verso monte il collegamento stesso. La variazione della capacità è dunque influenzata anche dal numero di corsie che si vanno a fondere a valle del collegamento (merge). Ad esempio, qualora si avessero tre corsie divergenti che convergono in una sola, ciascuna delle tre aventi un flusso di saturazione di 2000 veh/h/corsia, allora l’afflusso, da parte del collegamento in ingresso, sarà limitato a 6000 veh/h quando il collegamento a valle non è congestionato. Tuttavia, se si verificasse un incidente, la capacità della corsia potrebbe ridursi a solo 4000 veh/h. Su una sola corsia, oltre al gap si cercano anche eventuali ritardi tra i veicoli successivi che condividono l'uso della stessa corsia; mentre, in un approccio multi-corsia, i veicoli sono in grado di utilizzare le capacità residue delle restanti corsie. In conformità a quanto prevede tale logica, i veicoli procedono verso la loro destinazione, con la loro velocità e le posizioni longitudinali e laterali, sono aggiornate ogni decimo di secondo fino a quando il veicolo raggiunge il collegamento finale. Quindi, completato il percorso, il veicolo viene rimosso dalla simulazione; le statistiche sono tabulate e aggiornate, e le eventuali variabili temporanee sono assegnate.
La logica del modello, porta INTEGRATION a risolvere scenari in cui i tratti di strada si fondono (merge) in una o più corsie o si allontanano (diverge), tra di essi nascono anche delle zone di scambio (weaving) .
In generale, quando si fondono due flussi di traffico, tutta la capacità disponibile di fusione è assegnata in proporzione alla capacità della non-coda dei due link convergenti. Tuttavia, poiché una delle corsie della fusione non è in grado di utilizzare appieno il suo diritto, l'effettiva capacità di fusione deve sempre essere assegnata dinamicamente. Nel caso di una rampa di accesso, pertanto, si possono formare code a valle della rampa, o a monte della rampa sull’ autostrada, o su entrambi, a seconda dell’esigenza prevalente nello spostamento. Ad esempio, quando una corsia di accelerazione è presente, dopo la rampa, la coda sarà automaticamente modellata manifestandosi immediatamente a monte della corsia di discesa, Figura 2.6 (parte alta).
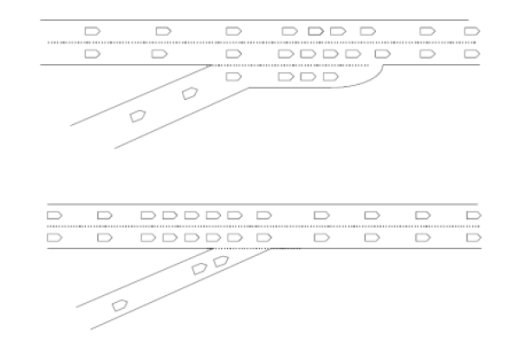
Figura 2.6: Congestion formation at a merge
La formazione della coda è chiaramente influenzata dalla modalità di arrivo dei veicoli. Tuttavia, se non vi è alcuna corsia di accelerazione, la coda si forma a monte della rampa, Figura 2.6 (parte bassa). Una volta determinate le percentuali di flusso convergente, INTEGRATION elabora le onde di shock a monte della fusione o sulla rampa principale. Inoltre, l'assenza di un intervallo di tempo definito nel modello di analisi consente la formazione di alcune code, che devono essere analizzate sia per brevi sia per lunghi intervalli temporali. Ad esempio, la formazione di code convergenti, su intervalli di tempo che vanno dai 15 minuti a diverse ore, possono essere modellate se sono stati considerati i sovraccarichi tipici del periodo di picco della domanda. Tuttavia, se a monte della rampa, è presente un segnale di traffico, il modello può anche considerare la sovrasaturazione a breve termine riferita ad intervalli di 30 - 60 secondi.
In caso di divergenza, le code si possono formare quando vi è una richiesta veicolare in ingresso superiore alla capacità. Tale limitazione nella capacità può essere dovuta, ad esempio, alla geometria della rampa di uscita o a un segnale stradale situato all’estremità di valle della stessa. Quando uno dei rami divergenti, ad esempio un impianto con rampa in uscita, possiede capacità insufficiente, i veicoli, destinati ad attraversare questo collo di bottiglia, formeranno la coda sulla sezione di monte della divergenza.
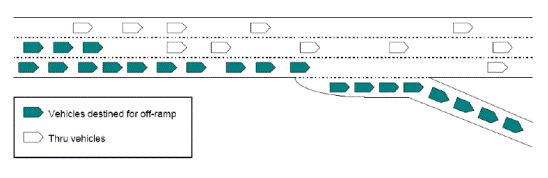
Figura 2.7: Queue formation due to an off-ramp
Di conseguenza, la coda formatasi costringe il flusso da una parte e non permette l’utilizzo della rampa di uscita. INTEGRATION calcola inoltre la conseguente coda di spillback come una funzione di sovra saturazione della rampa d’uscita, nonchè l’estensione dei veicoli che utilizzano la rampa d’uscita, i quali tendono a riunirsi nella corsia che alimenta tale rampa. Una conseguenza importante delle code spill-back nelle divergenze è che il link nel suo insieme non è più conforme alla logica delle code FIFO (First-In-First-Out).
In INTEGRATION le conseguenze finali del cambio di corsia sono funzione del modello di car-following e di lane changing. In particolare, si può osservare che i veicoli impegnati nella manovra di cambio corsia, occupano entrambe le corsie, sia quella di provenienza che quella da raggiungere, in [9].
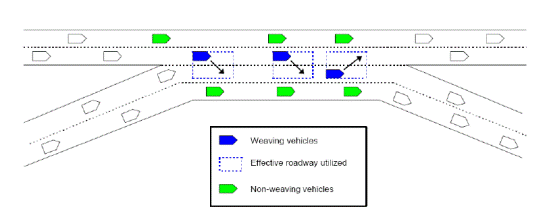
Figura 2.8: Capacity impact of weaving vehicles
Ciò si traduce in una momentanea variazione di capacità dovuta all’occupazione di uno spazio maggiore. Questo effetto, è proporzionale alla durata del cambiamento di corsia e alla frazione di veicoli che effettuano la manovra di cambio corsia. La riduzione effettiva di capacità nella sezione di manovra, in cui un gran numero di veicoli cambia corsia, non solo determina la formazione di coda, ma comporta anche una riduzione della velocità in tale sezione prima che la coda si manifesti. La capacità totale solitamente subisce anche un’altra riduzione dovuta al fatto che la disponibilità del lane changing gap non è uniforme ma casuale. Il modello è anche sensibile alla lunghezza della zona di cambio, in effetti, un tratto di strada più lungo per effettuare il cambio, influisce meno sulle dinamiche dei veicoli, in [10]. Pertanto, la riduzione di capacità, in quelle zone in cui un gran numero di cambi di corsia obbligatori sono necessari, dipenderà dai veicoli che effettuano il cambio rispetto al flusso in arrivo nella zona di cambio.
2.11 Implementazione e simulazione del software Integration 2.30
I dati d’input, richiesti dal modello, si distinguono in fondamentali e avanzati. I dati fondamentali sono essenziali per il funzionamento del modello mentre quelli avanzati consentono di sfruttare alcune caratteristiche opzionali del modello.
Tramite i file di input (file di testo con estensione .DAT) si devono fornire le indicazioni essenziali per la costruzione della rete, quali:
- Le coordinate, le caratteristiche e gli attributi dei nodi della rete;
- Le strutture, le caratteristiche e le coordinate degli archi;
- I piani di semaforizzazione;
- La domanda O/D di traffico;
- La descrizione degli incidenti;
- Informazioni addizionali fornite al programma dai file di input opzionali;
La struttura di tutti i file di input è sostanzialmente quella di una tabella, caratterizzata dalle presenze di righe e colonne. Ogni riga (esclusa la prima) rappresenta un componente dei file ed ogni colonna ne descrive le caratteristiche specifiche. La struttura delle righe è uguale per quasi tutti i file ma le colonne assumeranno sempre un numero ed un significato diverso. In questi file sono essenzialmente elencati:
- TITOLO: nome del file e suo utilizzo
- DATI: contatore del numero di oggetti elencati (righe) e fattori di scala per la visualizzazione grafica di Integration;
- OGGETTI: si susseguono i singoli componenti che avranno un numero di colonne prestabilito in base al tipo di file che descrivono. La prima colonna di ogni riga rappresenta il numero identificativo di ogni oggetto contenuto nel file.
Occorre precisare che l’implementazione dei file di input è la maggiore difficoltà per l’uso del programma di modellazione, non solo per la complicata comprensione delle righe di testo, ma anche per il dispendio di tempo, comunque è da ricordare che in fase di simulazione il programma riesce ad individuare gli errori e indicare i file di input dove sono stati commessi. I dati e i nomi saranno inseriti nei file d’input con caratteri ASCII in formato tabulato. I file d’input (Tabella 2.1) possono essere generati e modificati con qualsiasi redattore standard di testo o foglio di calcolo elettronico.
Il Master Control File fornisce al modello i parametri generali della simulazione e definisce i file di dati in entrata che saranno poi utilizzati. Indica anche dove sono localizzati gli input, definisce quali output saranno prodotti e dove questi saranno riportati. Per convenzione, agli archivi è assegnata tipicamente l’estensione .INT .
Il master file di solito è posto nella stessa cartella di destinazione dei file. In tal modo, non si dovrà indicare per intero il percorso della cartella di destinazione (es. INTGRATS TEST1.INT). In alternativa, se il MASTER FILE è allocato in una cartella differente o in una unità differente, il percorso completo deve essere specificato (es. INTGRATS D: \ TRAFFIC \ TEST1.INT). Tutti gli altri file dati, invece, sono indicati dall’estensione “.DAT” . Mentre tutti i file di output hanno come estensione finale: “.OUT”.
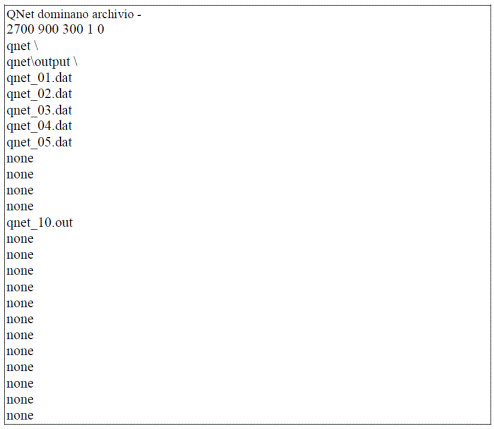
Tabella 2.1: Esempio di Master File con i fondamentali file di input e di output
Il Master file contiene tre tipi principali di dati. Il primo tipo è relativo alla linea 1 sulla quale si riporta il titolo del Master file, sulla linea 2 ci sono invece i parametri che definiscono tempo simulazione, frequenza, etc…
L’altro tipo di dati, contenuti nelle linee 3 e 4, descrivono le directory degli Input e degli Output. Le rimanenti linee contengono i percorsi di allocazione di Input e Output.
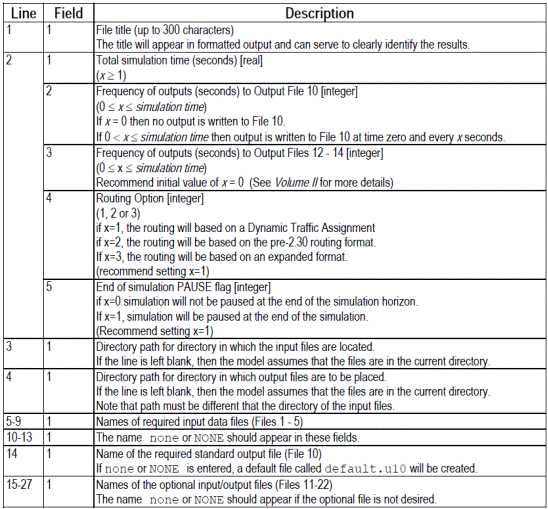
Tabella 2.2: Description of basic fields in Master Control File
La durata della simulazione è specificata sulla linea 2 ed è espressa in secondi. Questo valore dovrebbe essere sufficiente affinché i veicoli completino il loro percorso prima della fine della simulazione. La generazione dei file di Output provoca un intenso lavoro computazionale da parte del simulatore. Generalmente si sceglie un valore pratico per gli intervalli di Output (tipicamente 900 secondi). Il campo 5 della linea 2 ci consente di scegliere se stoppare la simulazione alla fine della stessa, allora si inserisce valore “0”, o 1 secondo prima della fine, quindi all’ultimo secondo della simulazione, allora si inserisce valore “1”.
2.11.2 File 1: caratteristiche del Nodo
Il File delle caratteristiche del Nodo specifica le coordinate X e Y di i nodi della rete. Elenca, inoltre, quali nodi sono intermedi lungo il percorso di un dato veicolo. A ciascun nodo deve essere assegnato un unico Numero Identificativo. Questi numeri possono non essere consecutivi e sequenziali. Per implementare la rete più grande possibile, è consigliabile adottare la convenzione che assegna numeri di nodo più bassi ai nodi origine e/o destinazione, lasciando i numeri più alti ai nodi intermedi. I Fattori di Scala sono utilizzati per modificare le coordinate X e Y dei nodi. Questi fattori moltiplicativi facilitano la trasformazione delle coordinate da un sistema di misura a un altro, come la trasformazione dal sistema miglia al sistema chilometri. I valori delle Coordinate X aumentano da Ovest ad Est, mentre il valori delle coordinate Y aumentano da Sud a Nord. Due nodi distinti non possono avere identiche coordinate X e Y.
I valori delle coordinate sono utilizzati dalla grafica del software, pertanto la loro inesattezza non pregiudica il risultato numerico della simulazione, tuttavia comprometterebbe la disposizione della rete sullo schermo. Nel rappresentare graficamente la rete, INTEGRATION tenta di massimizzare la quantità di schermo usato, sempre rispettando nell'aspetto un rapporto 1:1.
Le Macro Zone forniscono agli utenti un meccanismo per modellare le grandi reti del traffico risparmiando in termini di calcolo e di memoria. Ogni zona di destinazione deve essere associata a una macro-zona. Ogni macro-zona deve avere una sola zona di destinazione codificata come centroide di macro-zona. I nodi che non servono da destinazione devono avere il loro numero di macro-zona pari a zero.
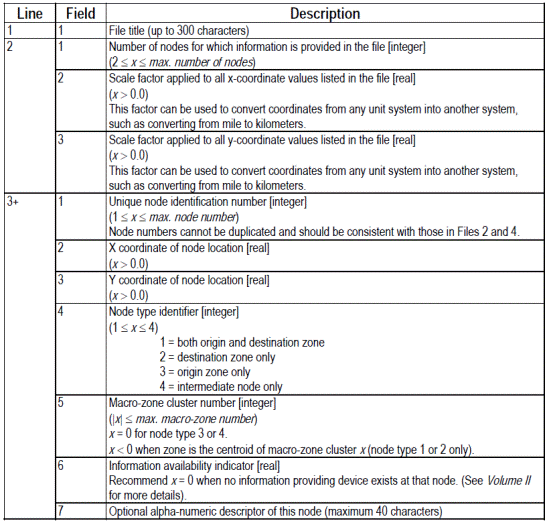
Tabella 2.3: Description of fields in Node Characteristic File (File 1)
2.11.3 File 2: caratteristiche dell’Arco
Il File delle caratteristiche degli Archi specifica i nodi alle estremità di ogni arco direzionale presente nella rete. Sono indicate inoltre le caratteristiche spaziali dell’arco, espresse dalla lunghezza e dal numero di corsie associate allo stesso. Le caratteristiche del flusso di traffico sono descritte in termini di grado di saturazione, velocità libera, velocità limite e densità limite. Nel settaggio della rete, a ciascun arco deve essere assegnato un unico Numero Identificativo. L'orientamento e la direzione di ciascun arco della rete sono definiti dai nodi che l’arco connette. I veicoli viaggiano lungo un arco dal nodo posto all’estremità superiore sino a quello inferiore. Nessuna coppia di archi può condividere gli stessi Nodi Superiore e Inferiore. La Lunghezza di un Arco è esplicitamente specificata. Per permettere al modello di riprodurre i cambi di corsia in modo realistico, dovrebbe essere evitato l’inserimento di archi molto corti. La lunghezza minima dell’arco permessa è una funzione del numero di corsie sull’arco ed è pari a 0,010 chilometri x numero di corsie. Così, la lunghezza di un arco con 3 corsie deve essere uguale o superiore a 30 metri. Questo valore rappresenta un minimo assoluto. La Capacità di un Arco è dedotta dal prodotto tra il numero di corsie specificate e il grado di saturazione per corsia. Questa capacità di base può essere ridotta per rispecchiare l'effetto provocato dai semafori, dalle rampe o dai flussi di traffico. Le velocità dei veicoli sono aggiornate continuamente durante la simulazione, grazie alla relazione Velocità-Flusso precedentemente illustrata. Questa relazione è dedotta dalla velocità libera, dalla capacità, dalla velocità limite e dalla densità limite, specificate dall’utente. La scelta di valori diversi di questi quattro parametri permette la derivazione di qualsiasi relazione velocità-flusso desiderata. Un Flusso di Traffico Opposto può limitare i movimenti dei flussi di traffico uscenti da un arco. INTEGRATION permette che siano specificati al massimo due potenziali flussi di traffico opponenti per ciascun arco. Per identificare questi flussi, l'utente deve esclusivamente individuare gli archi contenenti i flussi opposti, e non le svolte specifiche alle quali sono associati i veicoli opposti su questi archi. I controlli delle rampe possono essere modellati al meglio codificando una singola rampa come due archi separati posti in sequenza. Il primo arco può essere immaginato, in questo caso, come controllato da un segnale di traffico per la rampa. Quest’arco immagazzinerebbe la coda. Il secondo arco permetterebbe poi l'accelerazione dei veicoli dalla linea di stop sulla rampa sino all’area di convergenza con la rampa dell'autostrada.
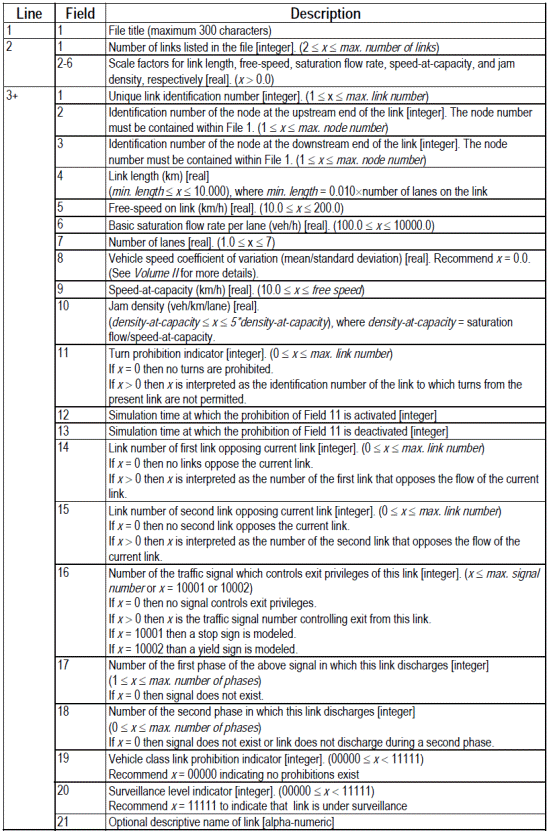
Tabella 2.4: Description of fields in Link Characteristics File (File 2)
2.11.4 File 3: Piani Semaforici
In INTEGRATION i semafori sono inseriti avvalendosi di un metodo articolato in due passi:
1. Il numero del semaforo che controlla ciascun arco della rete è indicato nel File2. Da default, possono essere specificate al massimo due fasi di scarico per ciascun arco.
2. Ciascuno schema delle fasi semaforiche nonché la durata dell'intervallo sono specificate nel File3.
In ciascun piano semaforico, i tempi dei segnali sono specificati in termini di lunghezza del ciclo, di offset della partenza della fase 1 e di numero di fasi nel ciclo semaforico. Sono forniti inoltre le durate dei tempi di verde e i tempi persi associati ad ogni fase. La struttura del modello permette che siano determinate un massimo di 8 fasi diverse per ciascun semaforo. Sebbene il file dei semafori d’esempio specifichi un solo piano semaforico per l'intera simulazione, con la stessa lunghezza di ciclo per tutti i segnali, nel modello non è necessario mantenere una lunghezza di ciclo costante per tutti i semafori all’interno di un dato piano. Non c’è inoltre bisogno che un segnale mantenga la stessa lunghezza del ciclo da un periodo all’altro. Di conseguenza, durante un dato periodo di controllo, i tempi di tutti i segnali possono essere coordinati usando una lunghezza di ciclo comune, oppure uno o più segnali possono operare isolatamente usando una o più lunghezze di ciclo. La scelta tra queste alternative, o qualsiasi loro combinazione, non deve essere affermata esplicitamente dal momento che, essa è implicita nelle specifiche del piano semaforico. Il semplice controllo a tempo fisso può essere modellato in INTEGRATION fornendo un singolo piano semaforico per l’intero periodo della simulazione. Il controllo a tempo fisso giornaliero può essere modellato fornendo diversi piani semaforici, ciascuno avente un tempo di funzionamento pari alla durata specificata dall’utente. Quest’ultimo può poi perfezionare un piano diverso per ogni ora, per ogni 15 minuti (900 secondi), o per qualsiasi altro intervallo di tempo desiderato, multiplo di 60 secondi.
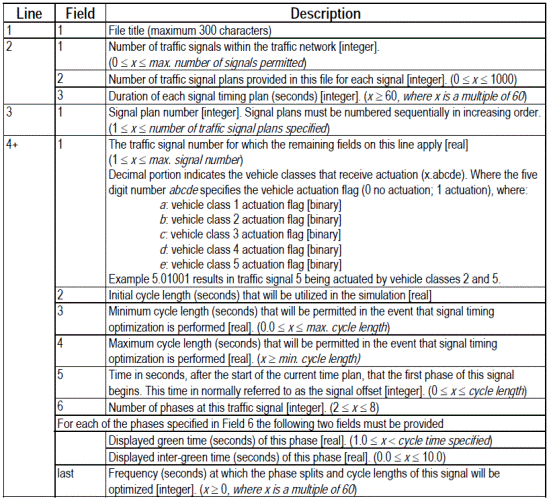
Tabella 2.5: Description of fields in Signal Timing Plan File (File 3)
2.11.6 File 4: domande di traffico Origine/Destinazione
La domanda di traffico è specificata nel modello INTEGRATION come una serie di flussi origine/destinazione in partenza. Durante la simulazione, le serie di partenze richieste sono scomposte in serie di partenze di singoli veicoli. Le domande di traffico sono specificate al modello in termini di flussi O/D in partenza e relativi a uno specifico set di zone origine/destinazione. Inoltre deve essere indicato il periodo di tempo all’interno del quale questi flussi sono attivi . Per esempio, se una domanda con flusso di 2500 vph parte al tempo 0, dopo 1800 secondi, questa domanda genererà un totale di 1250 veicoli (= (1800-0)/3600 x 2500). L'utente può specificare la composizione delle classi dei conducenti associati alla domanda, indicando la frazione di ognuna delle cinque possibili classi di conducenti. Durante la generazione dei veicoli, i conducenti sono assegnati casualmente ad una classe in funzione delle probabilità indicate.
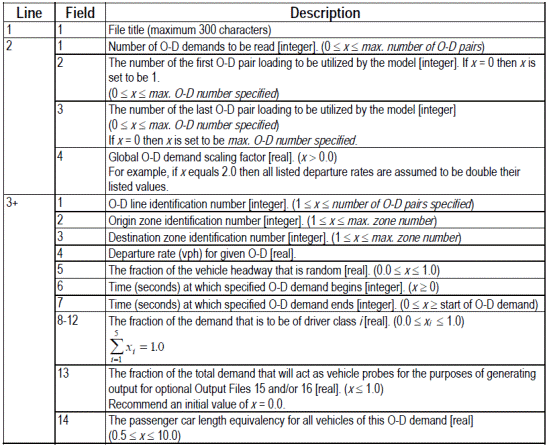
Tabella 2.6: Description of fields in O-D Traffic Demand File (File 4)
2.11.7 File 5: Incidenti o blocchi di corsia
Gli incidenti sono modellati come riduzioni temporali di capacità, tali riduzioni di capacità sono specificate come numero effettivo di corsie perse. Possono essere presi in considerazione molti incidenti allo stesso tempo su archi diversi, o in tempi diversi sullo stesso arco. Quando avviene un incidente, è modellato come se questo fosse stato causato all’estremità terminale dell’arco. La riduzione di capacità è calcolata in funzione del numero effettivo di corsie di traffico che si preveda vadano perse. Questo può essere un numero intero, per riflettere il blocco di corsia completa, o una frazione, per indicare un blocco parziale di una corsia. È anche possibile avere incidenti consecutivi sullo stesso arco. Comunque, è consigliabile non programmare incidenti multipli sullo stesso arco allo stesso tempo, o durante periodi di tempo sovrapposti.
Tabella 2.7: Sample Incident Descriptor File (File 5)
Il file della Tabella 2.7 descrive un incidente che blocca 1.5 corsie per 15 minuti (300 secondi) sull’arco 25, cominciando a 15 minuti (900 secondi) della simulazione. Di conseguenza, per 20 minuti (1200 secondi) nella simulazione, il veicolo è considerato accostato sulla banchina, dove blocca 0.75 corsie, e vi resta per altri 10 minuti (da 900 secondi a 1500 secondi).
Tabella 2.8: Description of the fields in Incident File (File 5)
2.11.8 Modello Output fondamentale
Il modello di INTEGRATION restituisce quattro tipi di output fondamentali, necessari alla comprensione della simulazione da parte dell’utente; questi sono:
1. Su schermo (Graphics)
2. Simulazione con eventuali errori (Runner.Out)
3. Statistiche della simulazione
4. Statistiche riassuntive (Summary.Out)
2.11.8.1 Su schermo (On Screen Graphics/text)
La finestra grafica di Integration mostra con continuità lo stato della rete. Questo output è estremamente prezioso poiché l’utente può controllare visivamente l’andamento della simulazione. La caratteristica di zoom, in particolare, può essere molto utile per valutare dettagliatamente i movimenti dei veicoli, nonché l’ubicazione e la durata di una eventuale congestione del traffico veicolare.
I movimenti dei veicoli che attraversano la rete sono visibili nella finestra grafica in quattro possibili colori. I conducenti che viaggiano a velocità di flusso libero, sono visualizzati sullo schermo con il colore verde. Quando la velocità scende, fino a raggiungere il valore relativo alla capacità dell’arco, il colore dei veicoli diventa azzurro. Appena al disotto di tale soglia il colore diviene giallo. Mentre quando si tendono a raggiungere delle velocità molto basse (formazione di code, congestione, etc…) il colore diventa rosso. Per esempio, i veicoli, che viaggiano su un arco avente una velocità a flusso libero di 100 km/h ed una velocità alla capacità di 60 km/h, sono verdi quando la loro velocità è compresa tra i 100 e gli 80 km/h, blu per una velocità tra gli 80 e i 60 km/h, gialli quando viaggiano tra i 60 e i 30 km/h e rossi per le velocità inferiori ai 30 km/h.
Alcuni incidenti sono mostrati come linee gialle, solitamente sono aggiornati sullo schermo in base al minuto corrente della simulazione. Una finestra aggiuntiva indica il numero dei veicoli che sono partiti allo stato attuale dell’interrogazione e il numero di veicoli che ha completato il percorso.
2.11.8.2 Simulazione con eventuali errori ( Runner.Out ).
Ogni qualvolta INTEGRATION inizia la simulazione il file Runner.Out viene automaticamente creato nella sub directory corrente. In questo file sono indicate:
- le informazioni riguardanti la costruzione della rete e quindi i file relativi alla microsimulazione, nonché le dimensioni degli array per il massimo numero dei nodi, il massimo numero di archi, etc;
- la lista di tutti gli eventuali errori che il software ha individuato durante la microsimulazione. Alcuni errori possono essere scoperti nel corso della microsimulazione o durante l’elaborazione dei dati, la descrizione degli errori commessi nei file offre uno strumento adeguato per la correzione dell’errore stesso. Alcuni errori “fatali” possono causare l’arresto della simulazione, altri invece sono da intendersi solo come avvertimenti e permettono al modello di proseguire la simulazione;
- diverse statistiche riferite alla fase di funzionamento del software.
2.11.8.3 Statistiche della simulazione
Le statistiche della simulazione sono generate nel file 10. Questo output è ideale quando è richiesta una semplice ispezione grafica della simulazione. In questo file sono riportati tutti i risultati della simulazione, gli step della simulazione e le caratteristiche degli archi con i relativi risultati, quali il tempo di percorrenza, la densità, il numero di veicoli, etc…
2.12.9.4 Statistiche riassuntive (Summary.Out)
Il quarto output prodotto dal modello INTEGRATION è un sommario di alcune importanti misure di performance a livello di rete globale. Quest’archivio è creato automaticamente ogni qualvolta è completato un giro di simulazione. Il primo gruppo di linee del Summary. Out addiziona tutti i veicoli appartenenti alle diverse classi. Il gruppo seguente di linee indica le misure medie calcolate dal rapporto tra il totale e il numero totale di veicoli appartenenti alla classe i-esima.
[1] INTEGRATION 2.30 User's Guide - Volume I: Fundamental Model Features.
[2] INTEGRATION 2.30 User's Guide - Volume II: Advanced Model Features.
[3] INTEGRATION: Overview of Simulation Features , M. Van Aerde , B. Hellinga, M. Baker and H. Rakha.
[4] INTEGRATION, Transportation Research Board 75th Annual Meeting, Washington, D.C.
[5] Rilett, L., and Van Aerde, M., (1991), Routing Based on Anticipated Travel Times, Application of Advanced Technologies in Transportation Engineering, Proceedings of the Second International Conference, ASCE.
[6] Velan, S., and Van Aerde, M., (1996), Relative Effects of Opposing Flow and Gap Acceptance on Approach Capacity at Uncontrolled Intersections,Transportation Research Board 75th Annual Meeting, Washington, D.C.
[7] US EPA, (1993), User's Guide to MOBILE5A: Mobile Source Emissions Factor Model.
[8] Baker, M., and Van Aerde, M., (1995), Microscopic Simulation of EPA Fuel and Emission Rates for Conducting IVHS Assessments, ITS America Conference,Washington, D.C.
[9] Van Aerde, M., Baker, M., and Stewart, J., (1996),Weaving Capacity Sensitivity Analysis using.
[10]Stewart, J., Baker, M., and Van Aerde, M., (1996), Analysis of Weaving
Section Designs using.
3.1 Descrizione del software SUMO TRAFFIC
"SUMO" è l’acronimo di "Simulation of Urban Mobility ". Questo microsimulatore della mobilità urbana è stato creato dai dipendenti del Centro per l'Informatica Applicata (ZAIK) e dall'Istituto di Ricerca sui Trasporti, presso il Centro Aerospaziale Tedesco. Il software è stato sviluppato in linguaggio C++ garantendo la portabilità sui vari sistemi quali Ms Windows, Linux, MacOS; il pacchetto completo quindi risulta disponibile in modalità Open-Source al fine di rendere i risultati facilmente comparabili ed anche al fine di agevolare la sperimentazione di algoritmi per la ricerca sul traffico e la mobilità. L’idea era quella di aiutare la comunità di ricerca sul traffico creando una piattaforma comune per testare e mettere a confronto i modelli di comportamento del veicolo con l’ottimizzazione semaforica, le rotte etc. I primi progetti in cui Sumo Traffic è stato utilizzato sono quelli riguardanti la gestione del traffico e le relative previsioni su grandi aree urbane.
Il modello microscopico sviluppato per le reti stradali contiene informazioni circa le connessioni tra corsie consecutive. Quando un nodo deve essere attraversato, i veicoli devono scegliere la corsia corretta per raggiungere quella desiderata. L’approccio utilizzato prevede la generazione automatica dei dati relativi alla realizzazione della simulazione, sia nel caso di una grande arteria autostradale che in quello di una piccola rete locale. A tal fine, oltre allo stesso programma di simulazione, il pacchetto Sumo include anche un programma che consente la conversione delle reti realizzate in altri formati. Questi formati sono propri di altre simulazioni, di tipo macroscopico o microscopico, o ancora provenienti da sistemi di routing. Nella simulazione macroscopica il flusso non è modellato utilizzando veicoli, ma in modo astratto e quindi senza corsie, in funzione essenzialmente della capacità della strada. La necessità, sia del calcolo automatico tra corsia e corsia che delle informazioni sui flussi opposti, risulta pertanto molto importante.
Figura 3.1: Two rather uncomplicated junctions
Due sono le riflessioni dietro il rilascio del pacchetto open source, in [1]. Per primo il fatto che ogni istituto di ricerca del traffico è costretto a realizzare un proprio pacchetto di simulazione; quindi alcuni sono interessati all’ottimizzazione dei semafori, altri cercano di trovare errori commessi durante la progettazione di una rete stradale. Perciò la prima idea era di fornire un quadro di base, contenente tutti i metodi necessari per una simulazione. La seconda è di avere un banco di prova per i modelli, in particolare i modelli di autovetture, e quindi rendere possibile un confronto all’interno della community. Ma, a causa dell’utilizzo di diverse architetture nella realizzazione dei simulatori del traffico, tali raffronti su larga scala non sono facili.
Quando si cerca di migliorare il traffico, risulta necessario un modello capace di lavorare a tale scopo. Anche se il traffico, nel suo complesso, può essere descritto dagli orari di partenza e dalle rotte con le rispettive durate, esso in realtà risulta fortemente condizionato dal desiderio di mobilità del singolo privato. Questo è un grande problema per la modellazione del traffico. In particolare il transito privato porta a un’impossibilità di descrivere il traffico con l'uso di formule matematiche. Si può asserire che il traffico è influenzato sia dal fatto che l’individuo desidera partire e arrivare in un luogo in un certo istante, sia dalla circolazione del veicolo sull’infrastruttura. In tal modo il traffico sulla rete dipenderà dal guidatore, ovvero dagli orari di partenza e dalla velocità di viaggio, ma anche da altri fattori come il meteo, eventuali incidenti, etc. Questa complessità rende poco agevole la ricerca di soluzioni adeguate a risolvere il problema, da qui la necessità di utilizzare degli opportuni e validi modelli matematici che tengano conto di tutte questi fattori. La simulazione è l'unico modo per mostrare i punti deboli della rete stradale o di prevederne il suo traffico. A questo scopo, molti pacchetti software di simulazione sono stati sviluppati. Tali pacchetti di simulazione del traffico differiscono sia nei modelli a cui si ispirano che nel loro schema: alcuni sono concepiti per essere utilizzati con le applicazioni Windows, mentre altri sono semplici strumenti da riga di comando. Modelli veicolari di questo tipo possono essere riferiti ad un tempo e ad uno spazio discreto, ovvero Cellular Automata, oppure possono essere discreti nel tempo e completamente continui nello spazio (Schreckenberg Nagel 1992, Brockfeld et al 2001).
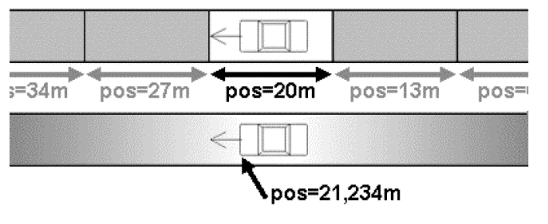
Figura 3.2: The difference between a space-continuous (top) and a space-discrete (bottom) simulation.
Nell’ambito della ricerca, ci imbattiamo spesso in pacchetti software già pronti per essere utilizzati (black–box) nelle loro specifiche applicazioni, ma che non consentono di modificare il codice sorgente. Inoltre, a causa delle diverse architetture software, un confronto tra le diverse caratteristiche dei modelli (come la simulazione della velocità, la sua capacità di descrivere la realtà, etc.) risulta difficile se non impossibile, in [2]. Al fine di proporre uno strumento che assolvesse a questi compiti non ancora svolti, l’istituto di ricerca sui Trasporti (IVF) insieme con il Centro per l'Informatica Applicata (ZAIK di Colonia, Germania) ha messo a punto questo software di simulazione del traffico open source chiamato Sumo Traffic. In realtà, questo software di simulazione del traffico è continuo, microscopico e multi-modale ed è anche in grado di modellare gli spostamenti su reti di dimensioni superiori a singole città. Il simulatore è in grado di riprodurre le reti di grandi città come Berlino, Monaco di Baviera e Colonia su un comune calcolatore. La maggior parte dei test sono stati eseguiti su PC Intel con funzionamento a 933MHz e aventi 256 MB di memoria. La simulazione è in grado di riprodurre i movimenti di circa 1 milione di veicoli per secondo in funzione della complessità della rete.
SUMO, implementato in C++, è stato progettato per essere veloce e preciso, pertanto se ne è trascurata l’estetica. Durante lo sviluppo, si è cercato di utilizzare solo parti standard del linguaggio di programmazione. Una di queste è quella STL che può essere scaricata gratuitamente.
Il codice è ben documentato, formattato e segue linee guide Ellemtel (Ellemtel 1990-1992), che assicurano la compatibilità con la maggior parte dei sistemi. Il software è compilabile con la maggior parte delle piattaforme e convalidato nei seguenti ambienti:
- Windows utilizzando MSVC + +;
- compilatore e STL-Port utilizzando Solaris SUN-C + +;
- Linux usando gcc.
3.4 Caratteristiche del software
In termini generali, la simulazione si svolge all’interno di uno spazio continuo in cui ogni veicolo segue il proprio percorso, mentre per simulare i movimenti sulla rete, è stato sviluppato un modello (di Krauss) che utilizza intervalli discreti di tempo pari a 1 sec. I veicoli che possono essere simulati in tempo reale sono anche 100000 con una macchina da 1 GHz, sono compresi la simulazione semaforica e i cambi di corsia. In sostanza quindi le caratteristiche di Sumo Traffic sono legate alla:
- Portabilità, ottenuta con l’uso del linguaggio standard C++ le cui librerie sono portatili;
- Open source, in altre parole licenza sotto GPL;
- Prestazione, cioè alta velocità di esecuzione e minima limitazione alla dimensione della rete e al numero di veicoli, quest’ultimo concetto consente:
- la libera circolazione di diversi tipi di veicoli;
- strade a più corsie con possibilità di cambiare corsia;
- incroci a base del diritto di modalità;
- gerarchia dei tipi di giunzione;
- gestione delle reti con più di 10.000 bordi (strade).
Gli elementi indispensabili alla simulazione sono invece i seguenti:
- la rete stradale;
- i veicoli con il relativo flusso;
- la segnaletica orizzontale e verticale.
Figura 3.3: Caratteristiche sumo traffic
Il software inoltre consente l'importazione di molti formati di rete (OpenStreetMap, Visum, Vissim, ArcView, descrizioni XML). Dalla versione 0.7 in poi, SUMO contiene le seguenti caratteristiche aggiuntive:
- un file output XML contenente le informazioni sullo stato della rete;
- detectors (valori separati per linee);
- file input XML che può essere ripartito su più file per una migliore gestione.
3.5 Modello alla base di Sumo Traffic
Sumo Traffic è concepito per simulare il traffico di una rete stradale delle dimensioni di una città. Poiché la simulazione è multi-modale, tale modello analizza non soltanto i movimenti delle auto all'interno della città ma anche i sistemi di trasporto pubblico, comprese le reti ferroviarie e gli spostamenti delle singole persone. Lo spostamento è descritto da un orario di partenza mentre il percorso si compone da rotte che descrivono il cammino compiuto.
In virtù di spostamenti multi-modali una persona può scegliere se lasciare la propria vettura alla più vicina stazione di trasporto pubblico e continuare il proprio viaggio con altri mezzi di trasporto.
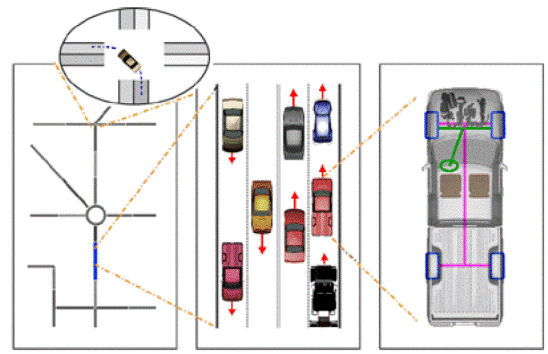
Figure 3.4: The different simulation granularities; from left to right: macroscopic, microscopic, sub-microscopic (within the circle: mesoscopic)
Da figura 3.4 si può evincere che il flusso veicolare è simulato a un livello di dettaglio microscopico, ciò significa che ogni veicolo che si muove sulla rete è visto dal simulatore come un oggetto che, in una certa posizione, possiede una certa velocità. Ogni passo della simulazione, ha una durata di un secondo, in tal modo i valori sono aggiornati in funzione delle caratteristiche del moto del veicolo mentre questo procede lungo la rete. La simulazione dei veicoli avviene in un tempo-discreto e in uno spazio-continuo. Anche il modello di car-driver è continuo, quindi si è deciso di utilizzare quest’approccio.
3.5.1 Comportamento del veicolo
Il modello risulta implementato su collision free e lane changing. La velocità del veicolo è funzione della velocità del veicolo che lo precede. Una distanza di sicurezza viene mantenuta tra i veicoli per prevenire le collisioni. Ad ogni step la velocità viene ricalcolata e adeguata alle esigenze del veicolo rispetto alle sue caratteristiche di accelerazione e decelerazione. Il modello consente inoltre di modificare le imperfezioni alla guida come l’andamento fluttuante della velocità del veicolo.
3.5.2 Lane-Changing e Car-Following
Il modello proposto ammette più di una corsia di traffico e più cambiamenti di corsia. Proprio come il modello di car-following, quello di lane-changing è a free collision, cioè si verificano dei cambi di corsia solo se il gap sull’altra corsia è abbastanza grande da garantire al veicolo una certa distanza di sicurezza durante il cambio. I cambi di corsia vengono eseguiti ogni qualvolta vi sia un vantaggio nel compiere la manovra (ad esempio il veicolo che precede è troppo lento ed il limite di velocità non è ancora stato raggiunto). Tuttavia, con una certa probabilità, il cambio di corsia può verificarsi anche senza che vi sia un vantaggio, ciò permette di modellare il comportamento umano, il quale è imperfetto. Il cambio di corsia è strutturato come un processo decisionale che analizza la possibilità di effettuare il cambio, la desiderabilità di farlo, e la fattibilità della manovra. Tutti questi fattori sono locali, in quanto dipendono dalla posizione del veicolo sulla rete stradale. Il comportamento del modello può essere sintetizzato con una serie di domande che descrivono il processo decisionale del guidatore che vuole cambiare corsia:
- È necessario cambiare corsia?
- È desiderabile cambiare corsia?
- È possibile cambiare corsia?
In quest’ottica il modello si avvale di una rappresentazione accurata della sezione, la quale viene distinta in tre zone (Figura 3.5).
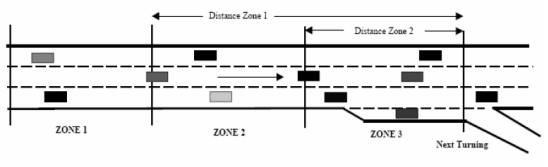
Figura 3.5: Modello di lane changing
A queste zone sono associati i parametri Percent Overtake e Percent Recover che rappresentano la percentuale di velocità desiderata, che il veicolo che segue e il veicolo che precede devono stabilire, se vogliono superare oppure rientrare nella corsia più lenta. Al suddetto modello di Lane Changing si unisce il modello di Gap Acceptance che individua appunto lo spazio necessario affinché possa realizzarsi il cambio di corsia; si è soliti far riferimento ad un gap critico, funzione della velocità relativa e dei distanziamenti da monte e da valle.
Invece, il modello di Car Following implementato in Sumo Traffic è basato sul modello di P.Gipps, in particolare lo si può considerare come uno sviluppo ad hoc del questo modello empirico. I parametri, alla base del Car-following di SUMO, non sono globali, ma influenzati da parametri locali dipendenti dal “tipo di guida”(limit speed acceptance del veicolo), dalla geometria della sezione (section limit speed, etc..), dall’influenza dei veicoli posti nelle corsie adiacenti, etc.. Il modello consta essenzialmente di due principali componenti, l’accelerazione e la decelerazione. La prima rappresenta l’intenzione del veicolo di raggiungere una certa velocità desiderata (principio che sorregge l’intero modello), mentre la secondo introduce le limitazioni imposte dal veicolo che precede, quando si cerca la velocità desiderata.
Il modello utilizzato di car–driver è in grado di descrivere
le caratteristiche principali sia del traffico congestionato che di quello a
flusso libero (free flow). Ad ogni passaggio la velocità del veicolo viene
adattata alla velocità del veicolo leader. Questa velocità è definita come
velocità di sicurezza (
),
ed è calcolata mediante la seguente equazione (1.3) :
(1.3)
dove:
(t)
è la velocità del veicolo al tempo t;
g(t) è il gap al tempo t;
è
il tempo di reazione del conducente (di solito 1s);
b è la funzione di decelerazione.
A seconda di come viene impiegata la capacità di accelerazione del veicolo, la velocità "voluta" o "desiderata" (2.3) è calcolata come il minimo tra la massima velocità possibile del veicolo e la velocità di sicurezza:
(2.3)
Inoltre, il comportamento del conducente viene riprodotto ipotizzando che egli compia degli errori, non riuscendo così ad adattarsi perfettamente alla velocità desiderata (3.3). Questo aspetto viene preso in considerazione sottraendo un "errore umano" casuale alla velocità desiderata:
(3.3)
La rete stradale in Sumo Traffic è rappresentata come una sequenza di nodi e bordi (archi). Il bordo, tratto compreso tra due nodi, rappresenta uno o diversi tratti di strada, che vanno nella stessa direzione. I nodi possono essere controllati da un semaforo (traffic light). Ogni semaforo può essere configurato singolarmente; se non ci sono dati disponibili sulla sequenza del semaforo, essa può essere generata automaticamente. Le priorità del bordo possono essere usate come input nel sequenziatore del semaforo in modo che l'uscita somigli il più possibile alla sequenza reale del semaforo. Per descrivere l’incrocio sono sufficienti poche informazioni. La sua posizione è individuata tramite un identificatore e nella maggior parte dei casi se ne deve indicare la priorità, quindi distinguere se si tratta di semplici incroci o di raccordi controllati da un semaforo. Inizialmente, il numero di corsie del singolo bordo dovrebbe esser dato. In caso di una simulazione macroscopica della rete, la capacità del singolo bordo deve essere utilizzata per calcolare il numero di corsie sul bordo stesso. Assumendo la capacità massima di una corsia pari a 2000 veh/h, la formula 3.4 consente di calcolare il numero di corsie, qualora questa informazione non fosse presente. L'unico inconveniente è che, in alcuni casi, i bordi utilizzati nella simulazione macroscopica della rete vengono caricati con flussi molto elevati in modo da conformare la simulazione alla realtà.
(3.4)
Altri attributi stradali, quali la velocità massima consentita, la lunghezza e altre informazioni geometriche, sono memorizzati direttamente all'interno del bordo.
I veicoli che utilizzano un arco che ha più di una corsia, devono scegliere la corsia da percorrere per raggiungere l’arco successivo. Occorre però un’ulteriore informazione: un veicolo si deve fermare prima di attraversare un incrocio, qualora un altro veicolo stia per sopraggiungere da un'altra direzione? Naturalmente, questo comportamento, dipende dal tipo di intersezione. Nel caso d’incroci controllati da un semaforo, tale comportamento sarà legato alle precedenze da esso create. In caso d’incroci non controllati, dipenderà tutto dalle priorità date alle strade che confluiscono nel bivio. Non consideriamo, per ora, eventuali segnali di stop.
Sumo Traffic prevede diversi approcci per le emissioni e i routing delle auto. In genere i veicoli sono associati a un percorso definito, che ha un certo orario d’inizio. Al dato istante di tempo il veicolo entra nella simulazione, inizia il suo percorso, segue la rotta e si ferma una volta che ha raggiunto la sua destinazione. Tali percorsi possono essere costruiti sulla base dei seguenti dati:
- dati random;
- dati di viaggio (trip);
- matrici origine / destinazione (O/D);
- raccordo con rapporti di svolta;
- induction loop.
I dati random permettono di creare la forma più semplice di rotte. Questi percorsi però non sono molto affidabili e dovrebbero essere utilizzati solo a fini di prova, in quanto per il generatore casuale del percorso, tutte le vie sono ugualmente importanti. In tal modo, le strade sono spesso utilizzate in modo sproporzionato rispetto al caso reale.
I dati di trip (viaggio) descrivono un singolo viaggio all'interno della rete. Le informazioni sul viaggio includono origine, destinazione e ora d’inizio del viaggio per il singolo veicolo. La generazione dei percorsi, basata sui dati di viaggio, richiede, pertanto, molte informazioni precise sulle attività dei veicoli nel mondo reale.
Una matrice O/D è una generalizzazione dei dati di viaggio. Essa contiene le stesse informazioni dei trip data, ma in via più generica, vale a dire piuttosto che dati esatti sulle origini e destinazioni, la matrice O/D è solita fornire solamente la zona di origine e quella di destinazione, permettendo una maggiore variabilità. Le matrici sono inoltre applicati a un certo numero di veicoli, e non al singolo veicolo. Le informazioni necessarie per costruire le matrici sono poche così come pochi sono i dati necessari alla costruzione dei percorsi relativi al viaggio. Tuttavia, un'idea generale circa gli spostamenti compiuti dalla popolazione è ancora necessaria.
I rapporti di svolta sfruttano invece coefficienti probabilistici, ovvero valori che descrivono la probabilità che un veicolo uscendo da un incrocio intraprenda una certa direzione. Gli itinerari possibili nel mondo reale possono essere calcolati utilizzando questi rapporti, anche in assenza di informazioni sul viaggio reale. In uno svincolo questo rapporto di svolta può essere ottenuto ad esempio mediante induction loop o da dati empirici. Se questi dati sono disponibili, le informazioni sul comportamento individuale non sono necessarie. Se gli induction loop sono distribuiti su tutta le rotte della rete, i flussi possono essere generati automaticamente. Tutti i metodi descritti in precedenza producono rotte statiche. Una volta che i percorsi sono calcolati i veicoli possono essere messi in rete automaticamente o con degli emettitori. Gli emettitori sono particolari fonti che possono essere collocate all’interno della rete. Possono emettere un unico flusso o più di un flusso di veicoli (un veicolo ogni time step). Gli emettitori sono in grado di operare una scelta probabilistica sia sui tipi di veicolo che sulle rotte. Vale a dire che un emettitore può essere configurato in modo che, ad esempio, emetta una piccola auto nel 70% dei casi e una grande auto nel 30% dei casi, ciascuno dei quali sarà scelto con una probabilità del 90% su di un percorso A e con il 10% su un percorso B.
3.7 Caratteristiche aggiuntive
Sumo Traffic supporta differenti tipi di veicoli. Ciò consente di modellare gli stessi con diverse proprietà fisiche (accelerazione, decelerazione, lunghezza, velocità massima), nonché conferire diversi privilegi ad alcune classi di veicoli. Le corsie possono essere configurate in modo che possano essere utilizzate solo da alcune categorie di veicoli, mentre ad altri sia vietato il transito. Vi è inoltre la possibilità di modellare i mezzi di trasporto pubblico, vale a dire le rotte e le fermate con le relative durate. Inoltre vi sono delle funzioni che consentono una simulazione più dinamica del mondo reale. Ad esempio, la segnaletica variabile consente l'adeguamento dei veicoli alle massime velocità su una strada o su una corsia, permettendo di sintonizzare il semaforo alla sequenza di traffico. Sumo Traffic offre due programmi per la simulazione: uno strumento da riga di comando e una versione grafica. Entrambe le versioni adottano lo stesso file d’input e creano lo stesso file di output. La versione grafica mostra la rete e permette di rintracciare i veicoli visivamente. La versione a riga di comando offre un'alternativa che consente una più rapida simulazione rispetto alla versione grafica. Sumo Traffic è realizzato con più di una singola applicazione. I seguenti moduli attualmente in fase di sviluppo sono:
Ø Sumo-Netconvert
Usiamo questo strumento per convertire i dati comuni, come gli elenchi dei bordi e dei relativi nodi in una rete completa simulabile dal software. Durante questo processo, Sumo-Netconvert legge i dati disponibili, calcola l'input necessario e scrive i risultati in un file “xml”. Nel frattempo, quattro diversi formati di input possono essere convertiti in rete Sumo:
- dati XML contenente i nodi, i bordi e la loro tipologia;
- dati Csv contenenti nodi, bordi e tipi di bordo;
- Cell file d’input (Cell è una coda di simulazione sviluppata dalla ZAIK);
- reti Visum.
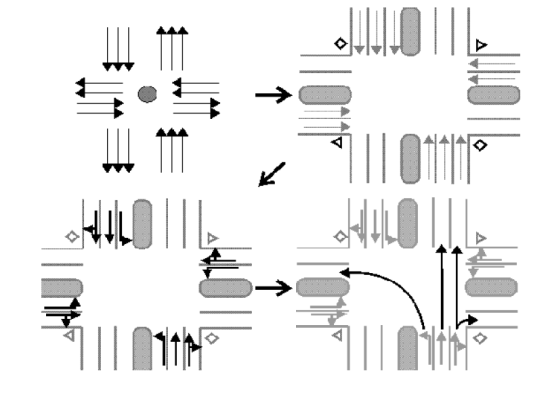
Figura 3.6: Conversion of simple, plain network data into a complete description
Ø Sumo-Router
Oltre alla parte statica rappresentata della rete, la simulazione è costituita da una parte dinamica relativa ai veicoli in movimento. In tali casi, sono utilizzati dei piani di rotte che descrivono lo spostamento dei veicoli. I dati necessari relativi all’istante di partenza e al percorso di origine e di destinazione dovranno essere indicati, al fine di calcolare i percorsi in un istante successivo. Questo calcolo viene effettuato utilizzando un modulo separato, ovvero Sumo-Router. Questo modulo legge i tempi di partenza, l’origine e la destinazione relativi ad un insieme di veicoli che vengono simulati, quindi calcola i percorsi utilizzando il noto algoritmo di routing di Dijkstra. Inoltre, poiché la velocità sulle strade cambia con la quantità di traffico, il calcolo del percorso viene effettuato utilizzando l’approccio del Dynamic User Equilibrium (DUA) sviluppato da Christian Gawron (Gawron 1998), dove il routing e la simulazione sono ripetuti più volte per ottenere un comportamento che più si avvicina a quello reale. Occorre notare che il router supporta il carico della rete in modo dinamico.
Per acquisire i dati dalla simulazione Sumo Traffic offre diversi tipi di rivelatori, che possono essere immessi nella rete. Gli induction loop possono essere utilizzati per raccogliere dati del veicolo come, ad esempio, la velocità media su un periodo di tempo arbitrario. Essi possono essere collocati su qualsiasi corsia e in qualsiasi posizione della stessa. I Lane based sono rivelatori usati per aggregare i dati su una corsia. I dati raccolti dal Lane based sono gli stessi dell'induction loop. I rivelatori multiorigine e multi-destinazione, invece, permettono la raccolta di dati arbitrari su parti della rete. Lo stato dump della rete restituisce i dati della stessa a ogni step, ciò include le informazioni su ogni corsia, compresa la posizione che i veicoli occupano e per quanto tempo essa la occupano. Sono raccolti anche i tempi medi di viaggio per tutti i veicoli della rete. I dati globali sui veicoli sono disponibili anche come: informazioni di viaggio generati una volta che un veicolo ha terminato il suo trip, contenenti tempo d’inizio e fine maggiorati di ulteriori valori, come i tempi di attesa per ciascun veicolo in viaggio.
3.9 Elementi aggiuntivi di Sumo Traffic
Le applicazioni più importanti incluse nel pacchetto Sumo traffic sono:
- Guisim, simulatore con interfaccia grafica utente;Netgen, generatore astratto di reti;
- Netconverter, generatore di reti basato sulla costruzione manuale;
- Dfrouter, applicazione che usa i flussi del rivelatore;
- Duarouter, assegnazione dinamica degli utenti;
- Jtrrouter, assegnazione tramite probabilità o rapporti di svolta;
- Sumo, applicazione per la simulazione.
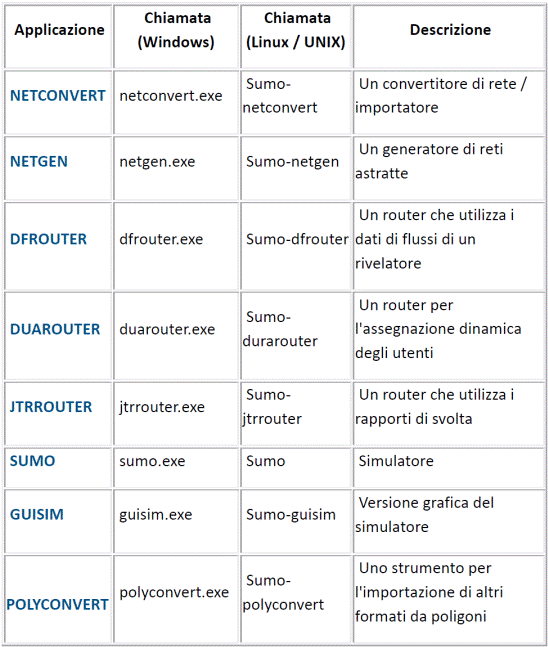
Tabella 3.: Applicazioni di Sumo Traffic
Una volta scompattato il file, nella relativa cartella è possibile trovare le applicazioni duarouter, netconvert, etc…, le quali, tutte tranne il Guisim, cioè l’interfaccia grafica con cui eseguire la simulazione, hanno bisogno di essere collocate tra le “variabili d’ambiente” di Windows. Esse infatti, essendo applicazioni Win32, devono essere lanciate tramite la linea di comando. Pertanto è necessario andare su “Proprietà del sistema”, cercare nel menù “Avanzate” le “Variabili d’ambiente” e ivi inserire il nome della variabile ed il suo valore (Figura 3.7).
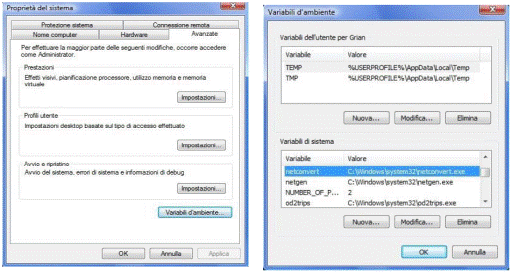
Figura 3.7: Proprietà del sistema e variabili d’ambiente
Fatto ciò è possibile eseguire le applicazioni, ad esempio tramite la finestra del Prompt dei comandi (Figura 3.8).
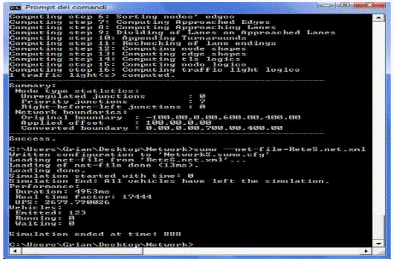
Figura 3.8: Prompt dei comandi
3.11 Preparazione della simulazione
È necessario eseguire la procedura sotto descritta, al fine di eseguire la simulazione. Occorre pertanto:
1. Creare la rete;
2. Costruire la domanda, è possibile fare ciò:
a) attraverso la descrizione esplicita delle rotte del veicolo;
b) utilizzando i flussi e le percentuali di svolta;
c) generando percorsi casuali;
d) attraverso l'importazione di matrici O/D;
e) attraverso l'importazione di proprie rotte.
3. Se necessario, calcolare l’assegnazione dinamica utente;
4. Eseguire la simulazione per ottenere il risultato desiderato.
Questo procedimento è illustrato in Figura 3.9.
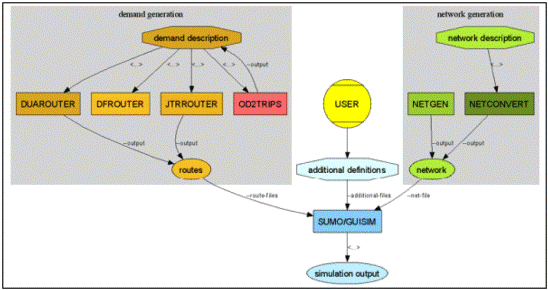
Figura 3.9: Process of simulation with SUMO; (rounded: definite data types; boxes: applications; octagons: abstract data types)
La generazione della rete, sulla quale verranno eseguite poi le simulazioni, può avvenire in diversi modi, in particolare attraverso l’uso di netgen e netconvert (Figura 3.10).
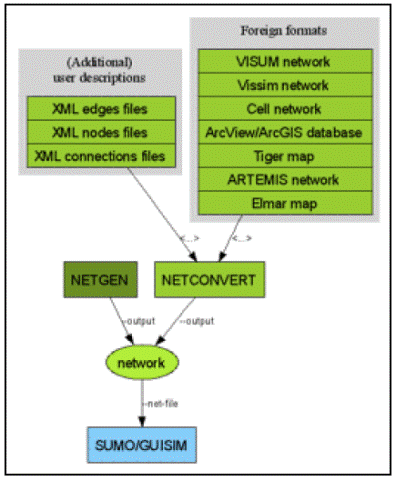
Figura 3.10: Building a network
1) Netgen, digitare direttamente dal prompt la stringa:
a) se si vuole realizzare una Griglia (con maglia regolare):
netgen --grid-net --grid-x-number=<int> --grid-y-number=<int> --grid
y-length=<int> --grid-x-length=<int> --output
file=MySUMOFile.net.xml
b) se si vuole realizzare una Spider-net (con un certo raggio):
netgen --spider-net --spider-arm-number=<int> --spider-circle
number=<int> --spider-space-rad=<int> --output
file=MySUMOFile.net.xml
c) se si vuole realizzare una rete Random:
netgen --random-net -o MySUMOFile.net.xml --rand-iterations=200 --abs-rand
2) Netconvert, in tal caso la rete viene generata inserendo quelli che vengono indicati come nodi (node) e bordi (edge); questi ultimi si ottengono tramite l’utilizzo di un opportuno editor di file xml (come ad esempio Visual C++). Ottenuti i bordi basta andare sul prompt dei comandi e inserire la stringa:
Netconvert --xml-node-files=MyNodes.nod.xml --xml-edge
files=MyEdges.edg.xml --output-file=MySUMONet.net.xml
in modo da convertire in un unico file di rete sia i nodi sia i bordi. Dallo stesso Netconvert inoltre si può creare una rete, attraverso l’acquisizione dei dati di altre applicazioni quali arcview, navteq, visum , etc.
Lo studio e l’implementazione della domanda sfruttano la conoscenza dei flussi di traffico e dei percorsi seguiti dai veicoli lungo la rete. Risulta quindi essenziale fornire i dati, sotto forma di lista, tramite l’editor dei file xml, ad esempio:
<routes>
<vtype id="type1" accel="0.8" decel="4.5" sigma="0.5" length="5" maxspeed="70"/>
<vehicle id="0" type="type1" depart="0" period=”10” repno=”100” color="1,0,0">
<route edges="beg middle end rend"/>
</vehicle>
</routes>
Le indicazioni più importanti riguardano:
- il tipo (type) di veicolo, ovvero accelerazione, decelerazione, lunghezza, max velocità;
- i dati riguardanti i veicoli lungo il percorso, ad esempio:
o depart : momento in cui il veicolo viene messo in rete;
o period: l’intervallo di emissione;
o repno : numero di veicoli che condividono lo stesso percorso.
- la rotta (route), ovvero i bordi attraversati dai veicoli.
Un modo alternativo di definire la domanda dei veicoli sulla rete e quello del Flusso, cioè:
<flows>
<flow id="0" from="edge0" to="edge1" begin="0" end="3600" no="100"/>
<flow id="0" from="edge0" to="edge1" no="100"/>
</flows>
In tal caso le indicazioni riguardano:
- i bordi (edge) superati dai veicoli;
- l’intervallo iniziale (begin) e finale (end) che, di default, varia tra ‘0’ e ‘3600’;
- e ‘no’, cioè il numero di veicoli da emettere in tale intervallo.
In quest’ultimo caso si utilizzerà l’applicazione Duarouter per ottenere il file di rotte:
duarouter --flows=<flow_defs> --net=<sumo_net>
--output-file=MySUMORoutes.rou.xml -b <int> -e <int>
Infine occorre considerare, sempre ai fini della creazione della domanda, le applicazioni:
- Jtrrouter, che consente di dividere i differenti flussi veicolari attraverso delle probabilità o delle percentuali di svolta;
- OD2Trips con il quale invece i dati vengono gestiti tramite una matrice origine/destinazione.
Per quanto concerne la simulazione, abbiamo bisogno sia del file della rete, ottenuto ad esempio con il Netconvert, sia del file delle rotte (route) dei veicoli, creato ad esempio con il Duarouter.
Avendo a disposizione questi dati è possibile utilizzare l’applicazione Sumo:
sumo --net-file=<file net> --route-files=<file route> --save-configuration=<nome file>.sumo.cfg
Tale applicazione ci consente di ottenere il file di configurazione necessario ad avviare la simulazione. Bisogna però fare attenzione e collocare tutti i file nella medesima directory. È possibile quindi visualizzare la simulazione attraverso l’applicazione grafica Guisim.
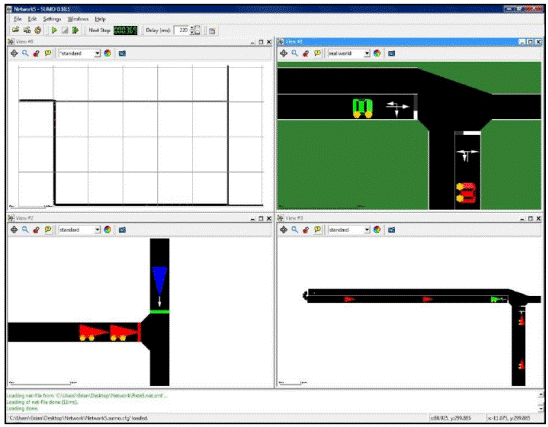
Figura 3.11: Interfaccia grafica Guisim
È possibile visualizzare, anche, i parametri riguardanti la rete, tra cui le velocità, i veicoli in ingresso e in uscita, la durata della simulazione, etc.
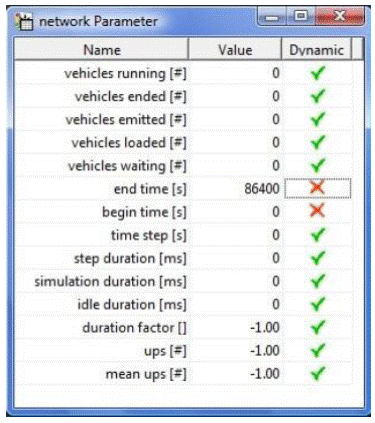
Figura 3.12: Parametri di rete
I parametri relativi ai singoli veicoli presenti sulla rete e le emissioni di CO2:
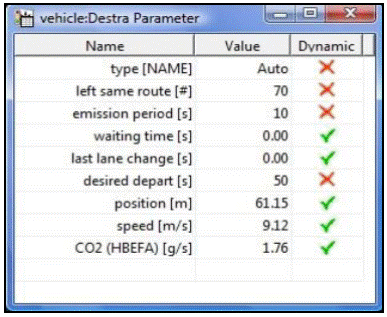
Figura 3.13: Veicoli sulla rete
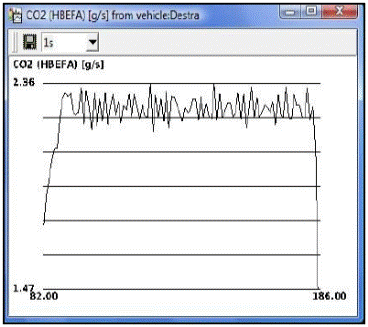
Figura 3.14: Emissioni di CO2
Tutti questi dati, infine, possono essere raccolti ed elaborati tramite, ad esempio, un comune spreadsheet.
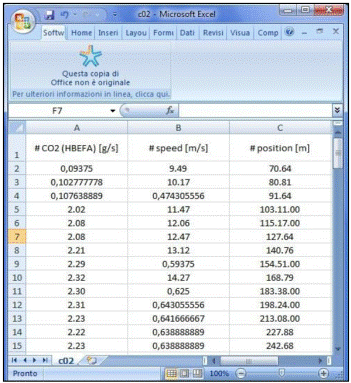
Figura 3.15: Spreadsheet
[1] SUMO (Simulation of Urban MObility); “An open-source traffic simulation”; Daniel Krajzewicz, Georg Hertkorn, Christian Rössel, Peter Wagner ; Proceedings of the 4th Middle East Symposium on Simulation and Modelling (MESM2002), SCS European Publishing House, pp. 183-187, 4th Middle East Symposium on Simulation and Modelling, Sept. 2002, Sharjah / United Arab Emirates.
[2] SUMO - Simulation of Urban MObility - User Documentation Daniel Krajzewicz, Michael Behrisch http://sumo.sourceforge.net/docs/documentation.shtml
4.1 Il modello microscopico alla base di AIMSUN
I grandi investimenti richiesti dai progetti realizzati in ambito trasportistico devono essere giustificati in modo adeguato. Pertanto sono necessari studi opportuni che dimostrino la validità dei propositi alla base di un intervento e che provvedano a condurre un’analisi costi-benefici senza trascurare gli impatti attesi. Ciò accade, in particolar modo, quando si vuole studiare il possibile sviluppo di Sistemi di Traffico Intelligenti (ITS), per individuare quelli che potrebbero essere i benefici derivanti dal loro utilizzo. I simulatori microscopici del traffico sono strumenti che simulano il comportamento reale di un flusso di veicoli (visti come singoli elementi) attraverso una rete stradale. Essi pertanto giocano un ruolo fondamentale all’interno degli studi di fattibilità nel campo dei trasporti. Ciò è dovuto non solo alla loro capacità di riprodurre tutte le dinamiche legate ai fenomeni del traffico dipendenti dal tempo, ma anche al fatto che essi utilizzano i modelli comportamentali che meglio descrivono le reazioni dei guidatori. In particolare, il microsimulatore AIMSUN, descritto in questo capitolo, è in grado di:
- rappresentare accuratamente la geometria della rete, grazie all’uso di Graphic User Interface, sul quale è possibile caricare anche mappe digitali di reti stradali;
- modellare dettagliatamente il comportamento dei singoli veicoli, grazie all’impiego di sofisticati modelli di car following e lane changing che prendono in considerazione sia i fenomeni globali che locali. L’attendibilità e l’alta qualità di questi modelli è stata comprovata in numerosi tests;
- riprodurre esplicitamente i piani di controllo del traffico. Interfacce ausiliari aiutano il simulatore a lavorare con diversi tipi di sistemi di segnaletica, come C-Regelaar, Balance, SCATS, SCOOT e UTOPIA;
- fornire animazioni 2D e 3D dell’output una volta avviata la simulazione. Questa non è solo una caratteristica squisitamente estetica ma può essere anche utile per capire le operazioni eseguite dal sistema ed individuare tempestivamente le problematiche.
I veicoli sono assegnati al percorso grazie a un modello di scelta del percorso. AIMSUN, acronimo di Advanced Interactive Microscopic Simulator for Urban and Non-Urban Networks, permette ai veicoli di cambiare, durante il viaggio, il percorso origine-destinazione al variare delle condizioni del traffico.
La recente evoluzione del simulatore microscopico AIMSUN ha tratto vantaggio dallo sviluppo dello stato del’arte dei simulatori orientati agli oggetti. L’interfaccia grafica del software si attiene alle nuove tendenze in materia di software design, rispondendo alle richieste, sempre più numerose, dei modellatori del traffico. Queste richieste, fondamentalmente, aspirano alla realizzazione di simulatori microscopici in grado di costruire modelli il più possibile vicini alla realtà. Ma più si vuole un modello aderente alla realtà, maggiori saranno i dati richiesti dal modello stesso. Tuttavia un elevato volume di dati potrebbe comportare, oltre che un eccessivo dispendio di tempo, una potenziale fonte di errore. AIMSUN cerca di ovviare a questo problema proponendo un’interfaccia User Friendly, molto versatile, che consente di importare sfondi di reti già esistenti e realizzati in vari formati, oppure di disegnare la rete direttamente, grazie ad un editor grafico. In particolare è possibile importare sfondi in formato .dxf file da sistemi CAD o GIS, ma anche file in formato .jpeg o bit map. Tutti gli oggetti, compreso il modello di rete, possono comunque essere costruiti con un editor grafico. Gli attributi e i parametri della rete vengono assegnati attraverso delle finestre di dialogo, come quelle mostrate in Figura 4.1.
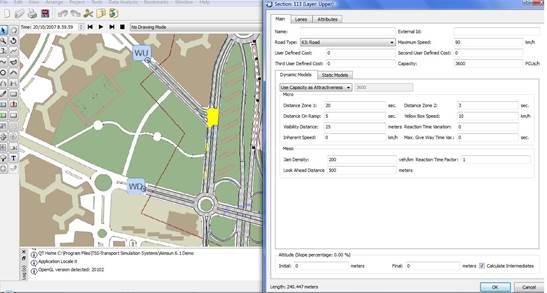
Figure 4.1: Example of AIMSUN graphic user interface for building microscopic simulation models.
Tutti i modi di trasporto possono essere virtualmente modellati con l’uso di alcuni veicoli tipo, corrispondenti al modello comportamentale. AIMSUN ci fornisce una libreria contenente i tipi di veicoli caricabili da default (Figura 4.2) ed un editor che invece permette di creare nuovi tipi.
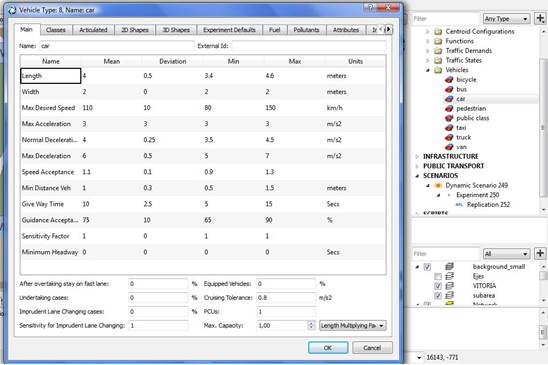
Figura 4.2: Vehicle types
Nella figura sopra è possibile vedere la finestra di dialogo all’interno della quale sono esplicitati i parametri relativi al tipo di veicolo auto (car). Una volta realizzata la simulazione di uno scenario di base, prima di usare il simulatore per applicazioni più sofisticate è necessario assicurarsi che questo riproduca le condizioni di traffico con un grado di accuratezza accettabile, in altre parole, che il simulatore emuli la realtà con accortezza. La calibrazione e la validazione di un modello microscopico sono operazioni che rivestono un ruolo importantissimo, al fine di assicurare che:
- il comportamento dei veicoli circostanti siano in accordo con i dati reali;
- gli output del modello comportamentale siano in accordo con i dati reali;
- a loro volta gli output macroscopici siano in accordo con i dati reali raccolti.
4.1.1 Modello di Car Following
Il modello di Car-Following implementato in AIMSUN è basato sul modello di Gipps, in [1]. I parametri del modello di Gipps non sono globali, ma influenzati dai parametri locali che dipendono dal “tipo di guida” (limite di velocità accettato dal veicolo), dalla geometria della sezione, dalle interferenze con i veicoli che si muovono sulle corsie adiacenti, etc. Esso consta di due componenti principali, accelerazione e decelerazione. La prima è associata all’intenzione del veicolo di raggiungere la velocità desiderata, la seconda, invece, alle limitazioni imposte al veicolo che cerca di procedere a tale velocità.
La versione 6.1 di AIMSUN introduce la minima distanza fra il veicolo di testa e il suo inseguitore come una nuova restrizione della componente di decelerazione alla base del modello Gipps. Questo vincolo è applicato prima che avvenga l’aggiornamento della velocità e della posizione del veicolo, ciò vuol dire prima di applicare l’equazione 1.10 del Capitolo 1:
Pertanto il vincolo di Minum Headway (distanza minima) è definito come:
(1.4)
dove:
è
la posizione del veicolo n-esimo al tempo t;
è la posizione del veicolo
che precede (n-1) al tempo t;
è
la lunghezza effettiva del veicolo (n-1);
è
la distanza minima del veicolo n dal suo inseguitore.
La versione 6.1 di AIMSUN considera la decelerazione del veicolo di testa come una funzione di un nuovo parametro a, definito a seconda del tipo di veicolo. A causa di questo parametro, chiamato ‘Sensivity Factor’, il modello diventa:
(2.4)
Quando a è minore di 1, il veicolo sottostima la decelerazione del veicolo di testa, diventando di conseguenza più aggressivo, riducendo il gap di inseguimento. Quando a, invece è minore di 1, il veicolo sovrastima la decelerazione del veicolo leader (di testa), diventando di conseguenza più prudente, incrementando così il gap con cui insegue.
4.1.2 Calcolo della velocità di un veicolo in una sezione
Il modello di car-following appena descritto è tale che un veicolo di testa, vale a dire un veicolo che viaggia liberamente, senza che gli altri veicoli possano influenzare il suo comportamento, cercherà di raggiungere la massima velocità desiderata. È possibile calcolare quest’ultima, mediante l’utilizzo di tre parametri, due dei quali sono relativi al veicolo ed uno, invece, è riferito alla sezione di manovra:
1. Velocità massima
desiderata del veicolo i-esimo: 
;
2. Velocità accettata dal
veicolo i-esimo: 
;
3. Velocità limite della
sezione di manovra s: 
.
La velocità limite del veicolo i-esimo sulla sezione di
manovra s, 
,
è calcolata come:
(3.4)
Allora la massima velocità desiderata del veicolo i-esimo
sulla sezione di manovra s, 
è
calcolata come:
Questa velocità massima desiderata è
la stessa di V*(n), contenuta nel modello di Gipps del Capitolo 1.
4.1.3 Il modello di car-following nel caso di doppia corsia
Quando un veicolo viaggia lungo una sezione dobbiamo considerare l’influenza, che un certo numero di veicoli (Nvehicles), che viaggiano più lentamente sulle corsie adiacenti, potrebbero avere sul veicolo in esame. Il modello calcola, per prima, la velocità media di un certo numero di veicoli posti a valle nella corsia adiacente più lenta (MeanSpeedVehiclesDown). Però solo i veicoli con una certa distanza (Maximum Distance) dalla corrente in esame, vengono presi in considerazione, vedi figura 4.3.
Figura 4.3: 2-Lanes car following
Distinguiamo due casi:
1) la corsia adiacente è una rampa di accesso (on-ramp);
2) la corsia adiacente ha la stessa tipologia dell’altra.
Oltre al Number Vehicles (Numero Veicoli) e alla Maximum Distance (Massima Distanza), l’utente può definire altri due parametri addizionali, Maximum Speed Difference e Maximum Speed Difference On-Ramp. Allora, la velocità finale desiderata da un veicolo su una sezione è calcolata come:
if (la corsia adiacente più lenta è una On-ramp) {
MaximumSpeed = MeanSpeedVehiclesDown + MaximumSpeedDifferenceOnRamp
}
else {
MaximumSpeed = MeanSpeedVehiclesDown + MaximumSpeedDifference
}
DesiredSpeed = Minimum (,
* MaximumSpeed)
Questa procedura garantisce che le differenze di velocità fra due corsie adiacenti siano sempre all’incirca minori della Maximum Speed Difference o della Maximum Speed Difference On-Ramp, a seconda dei casi.
L’influenza che la pendenza della strada ha sul movimento dei veicoli è invece modellata sulla base di un incremento o una riduzione di accelerazione e sulla capacità di frenata. L’accelerazione massima di un veicolo su una sezione, che sarà poi utilizzata nel modello di car-following, è funzione, quindi, della pendenza e della massima accelerazione desiderata dal veicolo:
accel = Maximum(vehicle_acc - slope*9.81/100.0, vehicle_acc*0.1)
Al fine di evitare valori negativi o nulli dell’accelerazione, è fissato un valore minimo della massima accelerazione desiderata pari al 10%.
4.1.4 Calibrazione del modello di car-following
Il modello di car-following di AIMSUN è stato testato e calibrato per una serie di casi reali; è di seguito illustrato il test eseguito dal gruppo di ricerca del Robert Bosch GmbH. Questo test, che ha sfruttato una serie di dati collaudati, vide la partecipazione dei maggiori architetti di micro-simulatori Europei e del Nord America, i quali furono chiamati a confrontare l’accuratezza delle misure e ad individuare le eventuali differenze tra le misurazioni e i valori simulati. Al fine di evitare eventuali sovrastime nel caso di grandi distanze fu scelto un metro quadratico e logaritmico:
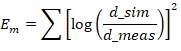
Dove d_sim è la distanza del veicolo simulato, d_meas è la distanza misurata dal veicolo test, e log denota il logaritmo di base 10. I risultati mostrano che il modello di car-following implementato in AIMSUN è in grado di riprodurre in modo fedele i valori osservati. I valori numerici dell’errore metrico, commesso dai principali modelli attualmente usati, sono riassunti in tabella 4.1.
Tabella 4.1: Comparative results of the Bosch Car-Following Test
MITSIM è il simulatore sviluppato dal MIT, Wied/Pel e Wied/Vis derivano rispettivamente dai modelli di Wiedemans/Pelops e VISSIM. NSM è il modello cellular automaton di Nagel-Schreckenberg, mentre i restanti due sono particolari modelli descritti in Manstetten et al.,1998b.
Fu condotto anche un secondo test per analizzare la qualità del simulatore, ovvero la capacità di questo di riprodurre i comportamenti macroscopici. Per questo test fu simulato il traffico su una strada ciclica ad una sola corsia, ciò al fine di evitare il cambio corsia e l’attraversamento di eventuali nodi. La strada ciclica aveva una lunghezza di 1000m ed il traffico era costituito da un numero fisso di veicoli, tutti della stessa lunghezza (4.5m) e tutti con la stessa velocità a flusso libero (54 km/h). il numero fisso di veicoli fu variato a passi discreti al fine di ottenere diverse densità di traffico. I risultati furono diagrammati in un grafico flusso-densità. I risultati di AIMSUN, relativi alla curva flusso densità simulata, furono confrontati con quelli empirici, rivelandosi ragionevolmente accettabili, vedi Figura 4.4.
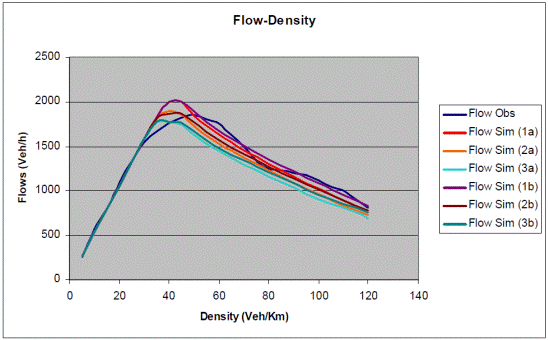
Figura 4.4: Empirical versus simulated flow-density curves
4.1.5 Modello di Lane-Changing
Il modello di cambio corsia implementato da AIMSUN può essere visto come un’evoluzione del modello di lane change di Gipps. Il cambio corsia è modellato come un processo decisionale che analizza la necessità di effettuare il cambio, la desiderabilità e le condizioni di fattibilità della manovra, quest’ultime sono locali e dipendono dalla posizione del veicolo sulla rete. Come abbiamo visto in precedenza il comportamento di questo modello decisionale risponde alla seguente domanda:
- E’ necessario cambiare corsia?
La risposta a questa domanda dipende da diversi fattori, quali la fattibilità della manovra se ci si trova su quella corsia, la distanza che intercorre dalla prossima svolta e le condizioni del traffico. Quest’ultime sono misurate in termini di velocità e lunghezza della coda. Quando un veicolo sta procedendo più lentamente di quanto esso sperasse, allora cerca di sorpassare il veicolo che lo precede. D’altra parte, quando il veicolo viaggia più velocemente di quanto desidera, esso tende a rallentare e a rientrare nella corsia meno veloce. Comunque se la risposta alla domanda è affermativa, allora bisogna rispondere ad altre due domande:
a) È desiderabile cambiare corsia? Il guidatore risponderà affermativamente se il cambio di corsia è in grado di apportare un miglioramento in termini di velocità e distanza.
b) È possibile cambiare corsia? Per rispondere positivamente occorre verificare che vi sia un gap sufficiente per eseguire la manovra in sicurezza. In particolare il cambio di corsia è possibile se la frenata imposta dal veicolo immediatamente a valle e la frenata causata al veicolo immediatamente a monte, hanno valori accettabili.
Al fine di avere una rappresentazione più accurata del comportamento del guidatore che esegue un cambio di corsia, la sezione stradale viene suddivisa in tre zone, in ognuna delle quali la manovra di lane change ha motivazioni diverse. Le zone sono caratterizzate dalla loro distanza dalla fine della sezione, cioè dal punto che indica la svolta successiva. La figura 4.5 illustra la struttura di queste zone, le quali sono definite nel modo seguente:
Zona 1: questa è la zona più lontana dal next turning point (punto di svolta successivo). La decisione di cambiare corsia dipende dalle condizioni del traffico e per misurare i vantaggi che il guidatore può ottenere dal cambio occorre considerare diversi parametri, quali la velocità desiderata, la distanza e la velocità del veicolo che precede e di quello che precederà una volta effettuata la manovra.
Zona 2: questa è la zona intermedia dove il cambio corsia è principalmente influenzato dalla corsia di manovra desiderata. I veicoli che viaggiano su una corsia non adeguata, cioè che non consente di effettuare la prossima svolta, tendono ad avvicinarsi al lato della strada dove la manovra è permessa. In questa zona i veicoli cercano un gap per inserirsi senza curarsi del comportamento dei veicoli sulle corsie adiacenti.
Zona 3: questa è la zona più vicina al next turning point. I veicoli sono costretti a lasciare la corsia desiderata, riducendo se necessario la velocità.
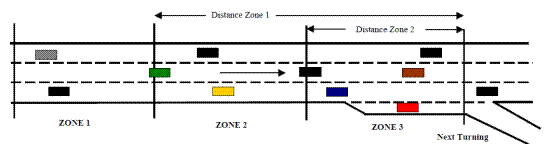
Figura 4.5: Lane Changing Zones
Le zone di cambio sono definite da due parametri, Distanza da Zona 1 e Distanza da Zona 2. Questi parametri sono espressi in secondi e vengono convertiti in distanze in un istante successivo. Quando un veicolo passa dalla zona 1 alla zona 2, si verifica un cambiamento nelle regole comportamentali dello stesso e diventa rilevante la prossima manovra. Anche nel passaggio dalla zona 2 alla zona 3 si assiste a questo cambiamento di comportamento, infatti in questo caso è urgente raggiungere la corsia che consente la prossima svolta. Al fine di distribuire questi differenti comportamenti su una lunga distanza è stata conferita alle zone di lane changing una grande variabilità. In particolare, queste zone sono calcolate per ogni veicolo con la seguente equazione:
Distance Zone n for vehicle v in section s (in meters) =
= Distance Zone n (in seconds) * Speed Limit of Section s * Vehicle v Coefficient
Vehicle v Coefficient = Speed Limit of Section s / Desired speed of Vehicle v in section s
Questo algoritmo assicura che le zone di cambio corsia dei veicoli la cui velocità desiderata è più bassa del limite consentito siano più lunghe rispetto a quelle dei veicoli che hanno una velocità desiderata maggiore del limite. Ciò significa che un camion pesante guadagnerà la corsia appropriata prima di un’auto veloce.
4.1.5.1 Look Ahead
Quando le condizioni del traffico sono molto congestionate, potrebbe accadere che alcuni veicoli non riescano a raggiungere la corsia adeguata, rinunciando così alla manovra successiva. Questa situazione si verifica spesso nelle reti urbane dove le sezioni sono molto corte, ma anche sulle autostrade dove le sezioni di weaving potrebbero essere molto ridotte. Regolando alcuni parametri quali la distanza delle zone di lane changing, gli step di simulazione e il grado di accelerazione, si potrebbe migliorare il comportamento al fine di minimizzare il numero di veicoli persi. Il problema si potrebbe risolvere anche utilizzando una geometria multi sezione, ma non è detto che tutti questi accorgimenti sortiscano un effetto positivo. Per ovviare a questi inconvenienti il modello di lane changing è stato migliorato attraverso un processo di Look Ahead. L’obiettivo è quello di fornire ai veicoli la conoscenza necessaria, relativa alle varie manovre e non solo ad una, in modo che il veicolo sia capace di decidere, non sulla base di un’urgenza (eseguire la svolta), ma sulla base di tutte le manovre che dovrà poi compiere. Il Look Ahead si compone di quattro passi:
1. In qualsiasi istante, ciascun veicolo conosce la prossima manovra, in modo che la decisione di cambiare corsia sia influenzata da due manovre successive.
2. Le zone di lane changing 2 e 3 di ciascuna sezione si estendono ben oltre i limiti della sezione stessa, influenzando pertanto le sezioni di monte.
3. La svolta successiva influenza la manovra in modo che la scelta della corsia di destinazione sia fatta in funzione di essa.
4. La zona di lane changing possiede una grande variabilità al fine di distribuire le manovre di cambio corsia su una lunga distanza.
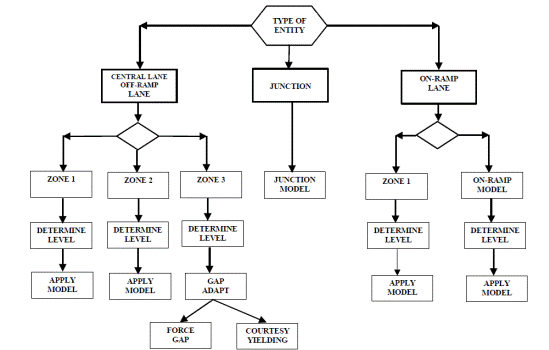
Figura 4.6: Lane changing decision tree
4.1.5.2 Il modello di lane changing per una rampa di accesso (On-Ramp)
Uno speciale modello di cambio corsia è applicato alle rampe di accesso. In questi casi viene definito un parametro addizionale di zona, TimeDistanceOnRamp. Questo parametro rappresenta la distanza da quelle corsie laterali che sono proprio le corsie della rampa di accesso, ciò al fine di distinguere tra le comuni corsie laterali, usate per il sorpasso, e quelle della on-ramp, che non possono essere impiegate per tale scopo. I veicoli, che viaggiando su una corsia laterale, si trovano più lontani rispetto al TimeDistanceOnRamp dalla fine della sezione, si comportano come se si trovassero nella Zona1di una normale corsia. Quando invece, essi sono più vicini del Time DistanceOnRamp alla fine della corsia, si comportano come se dovessero proseguire (merge) sulla rampa di accesso. Il modello Merge OnRamp analizza se un veicolo è fermo o meno, e, qualora fosse fermo, cerca di capire se si è fermato all’inizio della rampa o meno, e da quanto tempo aspetta. A tal proposito vi è il parametro, Maximum Waiting Time, che ci dice quanto tempo il veicolo è disposto ad aspettare prima di diventare impaziente.
4.1.6 Il Modello Gap Acceptance di AIMSUN
Vi sono due situazioni tipiche in cui il Gap Acceptance potrebbe essere applicato:
- nel lane changing;
- nel modello comportamentale give way.
Gap Acceptance Model in Lane changing
Per rispondere alla domanda ‘È possibile cambiare corsia?’ AIMSUN applica il seguente algoritmo per capire se il gap è accettabile o meno, Figura 4.7.
Figura 4.7: gap acceptance algorithm in lane changing
Gap Acceptance Model in give way
Il modello di Gap-Acceptance impiegato nel modello comportamentale del give way (dare precedenza) stabilisce se un veicolo che raggiunge un incrocio con una priorità bassa può o non può attraversarlo, tenendo presente le esigenze dei veicoli con priorità più alta (posizione e velocità). Questo modello considera la distanza dei veicoli dal loro ipotetico punto di collisione, la loro velocità e il loro grado di accelerazione. È possibile calcolare quindi il tempo necessario al veicolo per attraversare l’intersezione e decidere se passare o meno in funzione del livello di rischio. Diversi parametri potrebbero influenzare il comportamento del modello di gap-acceptance: velocità desiderata, velocità accettata e massimo tempo di give-way. Ma anche altri parametri, quali la distanza di visibilità all’intersezione e la velocità di svolta, legati alla geometria della sezione, potrebbero avere una certa incidenza sul comportamento. Il tempo massimo di give-way è utilizzato per determinare il momento in cui un guidatore diventa impaziente non riuscendo a trovare un gap adeguato. Quando il guidatore ha superato questo tempo di attesa, tende a ridurre il margine di sicurezza della metà. Il seguente algoritmo è applicato per stabilire se il veicolo VEHY attraversa o non attraversa l’intersezione di Figura 4.8:
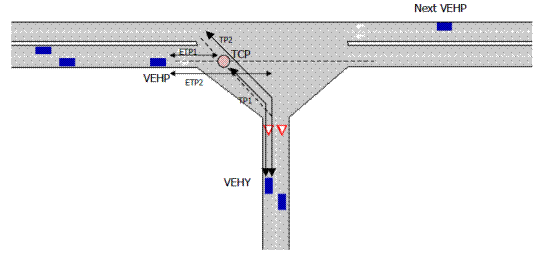
Figura 4.8: Junction
Given a vehicle (VEHY) approaching a Yield (Give Way) junction,
- Obtain the closest higher priority vehicle (VEHP),
- Determine the Theoretical Collision Point (TCP),
- Calculate the time (TP1) needed by VEHY to reach TCP,
- Calculate the estimated time (ETP1) needed by VEHP to reach TCP,
- Calculate the time (TP2) needed by VEHY to cross TCP,
- Calculate the estimated time (ETP2) needed by VEHP to clear the junction,
If TP2 (plus a safety margin) is less than ETP1, vehicle VEHY has enough time to cross, therefore it will accelerate and cross,
Else, if ETP2 (plus a safety margin) is less than TP1, vehicle VEHP will have already crossed TCP when VEHY reaches it, then search for the next closest vehicle with a higher approach, Next VEHP and go to step 2.
Else, vehicle VEHY must give way, decelerating and stopping if necessary.
4.2 Implementazione e simulazione
In questo paragrafo sono descritti i passi da eseguire per realizzare una rete stradale completa, in ambiente AIMSUN, partendo da zero, in [2]. Sono pertanto indicati i dati obbligatori da inserire al fine di avviare la simulazione della rete. Definiremo, passo dopo passo, basandoci su una serie di immagini, tutti gli elementi grafici che compongono una rete, comprese le sezioni, i nodi, le rotatorie, le corsie e la segnaletica. Vedremo anche come inserire i centroidi e le matrici O/D.
Il primo passo da eseguire è creare, dopo aver acceso AIMSUN, un nuovo modello; ciò può essere fatto usando il menu File/New. Selezionare il default template.
Figura 4.9
Questo template inserisce degli oggetti da default nella finestra di progetto (project), come si può vedere nell’immagine seguente:
Figura 4.10
L’utente ha la possibilità di creare nuovi oggetti e salvarli in un template per i progetti futuri.
E’ possibile importare un’immagine sulla quale poi creare la rete, tuttavia questa scelta è facoltativa. Ad esempio, in questo caso, abbiamo importato un file .DWG (CAD drawing) e un’immagine JPG. Per fare ciò si può usare il menu File/Import:
Figura 4.11
Iniziamo con l’importare il file DWG, Background_Small.dwg, che si trova nella cartella Exercise, impostiamo la tendina Geo Units su Meters, mentre quella Encoding su System, poi selezioniamo dal menu principale View/Whole World.
Figura 4.12
Ora è possibile selezionare il menu Window/Windows/Layers e andando sui layers è possibile spegnerli o accenderli, modificare il colore delle linee, o selezionare parti del disegno, cambiandone lo stile o l’aspetto.
Figura 4.13
Fatto ciò, importiamo l’immagine image.jpg andando su File/Import/Image File e quindi selezioniamo dalla directory Exercises l’immagine image.jpg.
Una volta aperta l’immagine, è possibile posizionarla correttamente sul modello utilizzando l’opzione denominata placer. Basta fare doppio click sull’immagine e si aprirà la finestra Placer. Una volta posizionata l’immagine, onde evitare che questa possa essere accidentalmente mossa, è meglio bloccare il layer. Per fare ciò basta cliccare due volte sul layer Images e deselezionare l’opzione Allow Object Editing.
Ora possiamo iniziare a creare la geometria della rete all’interno dell’area rossa evidenziata nella figura sottostante, dove molte sezioni sono già state create:
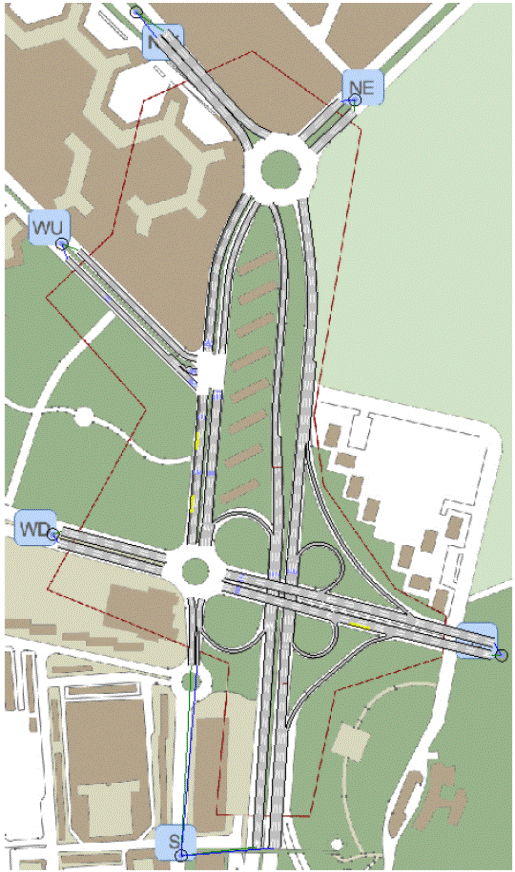
Figura 4.14: Vista Generale
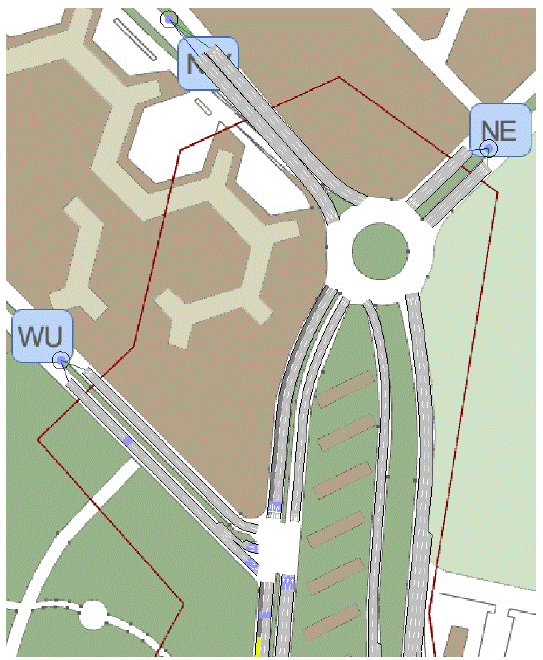
Figura 4.15: Zoom 1
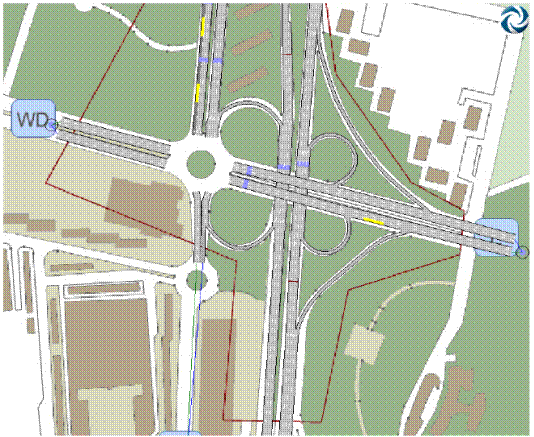
Figura 4.16: Zoom 2
Aggiungere una sezione
Per aggiungere una sezione occorre selezionare il bottone
‘create section’ 
dalla
barra dei comandi posta sul lato sinistro dello schermo, cliccare quindi con il
tasto sinistro nel punto in cui la sezione deve iniziare, poi cliccare due
volte, sempre con il sinistro, nel punto in cui la sezione finisce.
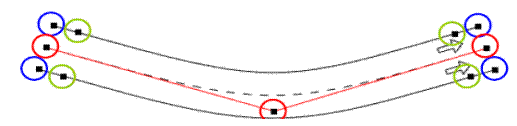
Figura 4.17
La posizione della sezione può essere modificata trascinando i punti posti sulla sua linea media, i quali sono visibili una volta che la sezione è selezionata.
Crea un nuovo vertice, utilizzando rettilinei o tratti di curva
Le sezioni possono essere costruite usando il tasto New
(Straight 
or
Curve 
)
Vertex. Il primo è riferito a segmenti rettilinei ed è possibile aggiungere
alla sezione quanti vertici si vogliono. Per aggiungere un nuovo vertice,
occorre prima selezionare la sezione, poi cliccare sul tasto New Vertex, quindi,
tenendo premuto il tasto sinistro del mouse, trascinare una linea che interseca
la sezione nel punto ove si vuole il vertice.
Aggiungere corsie
Per creare o rimuovere le corsie laterali si devono utilizzare i punti esterni, cerchiati in verde nella figura di seguito. Trascinando questo punto è possibile aggiungere la corsia e poi modificarne la lunghezza.
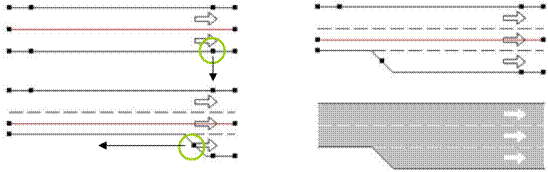
Figura 4.18
Congiungere le sezioni
Se si vogliono congiungere delle sezioni, è necessario prima selezionarle tutte, poi cliccare con il tasto destro, quindi scegliere dalla tendina che appare il comando join, oppure in alternativa si usi [Ctrl+M].
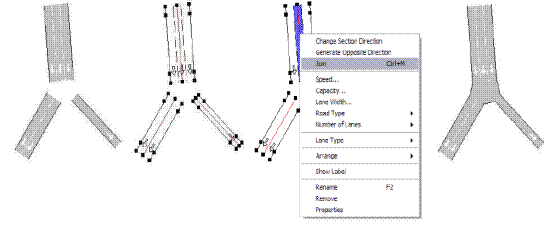
Figura 4.19
Creeremo i nodi con geometria mancante, cioè quelli che sono indicati nella figura di seguito.
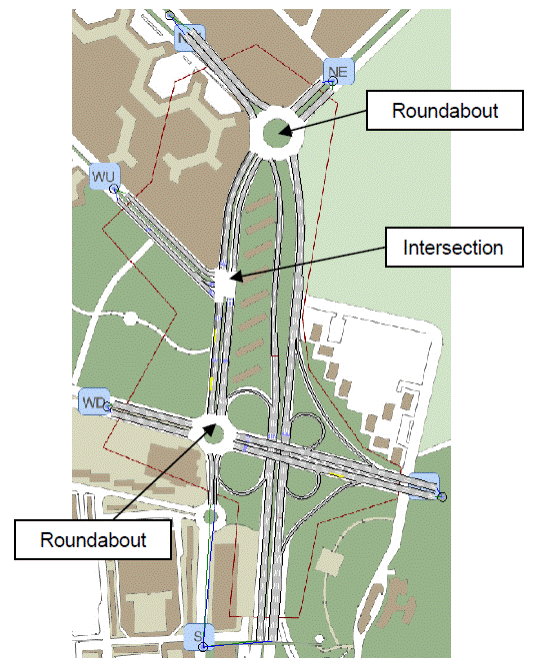
Figura 4.20
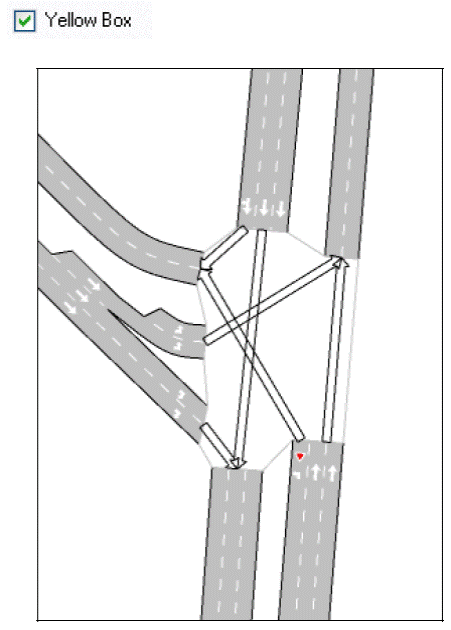
Figura 4.21: Intersezione
Al fine di creare un’intersezione dobbiamo cliccare
sull’icona di creazione del nodo 
in
modo da visualizzare l’editor del nodo. Le manovre devono essere inserite una
per una, cliccando su New all’interno della tabella Main dell’editor
dei nodi. Usando il mouse, selezionare prima le corsie sulla sezione di origine
della svolta e, successivamente, le corsie della sezione di destinazione.
Il modo più veloce per attivare il Give Way su svolte diverse consiste nel selezionare il nodo e, dopo aver selezionato tutte le svolte che hanno la restrizione, cliccare con il tasto destro del mouse per accedere al context menu, quindi scegliere l’opzione Give Way, come mostra la seguente immagine.
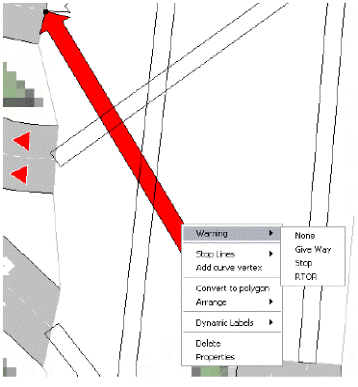
Figura 4.22
È possibile regolare la priorità anche in un altro modo, cioè aprendo la finestra di dialogo del nodo e selezionando Give Way nella colonna Warning della svolta corrispondente.
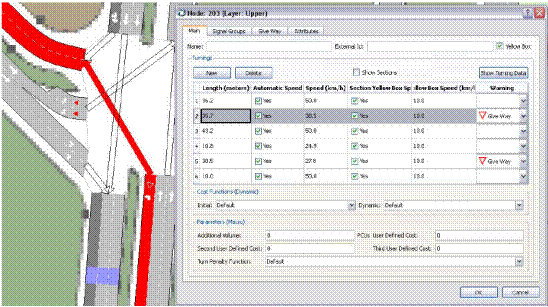
Figura 4.23
Rotatorie
Al fine di creare una rotatoria, potremmo usare il tasto
Roundabout 
nel
modo seguente:
- selezionare tutte le sezioni entranti ed uscenti dalla rotatoria;
- premere il tasto Roundabout e cliccare nel punto in cui si vuole il centro della rotatoria;
- muovere il mouse per stabilire il raggio della rotatoria;
- mentre si tiene premuto il mouse, è possibile cambiare il numero delle corsie della rotatoria premendo CTRL+[numero di corsie] (1,2,3,…,7).;
- rilasciare il mouse per creare tutte le sezioni che costituiscono la rotatoria.
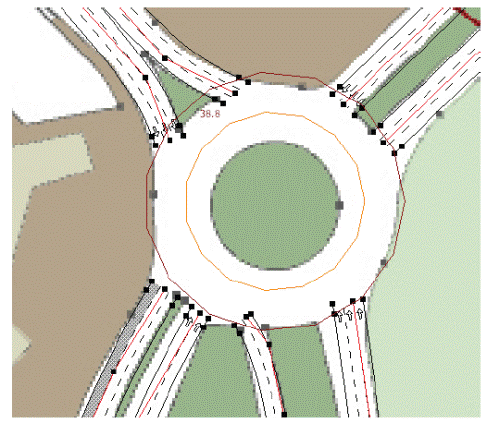
Figura 4.24
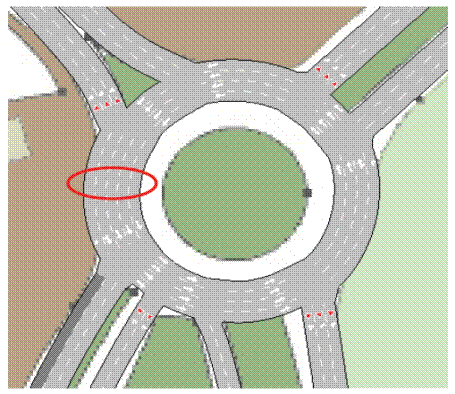
Figura 4.25
Nelle intersezioni, al fine di rendere più realistico il movimento dei veicoli è possibile utilizzare l’opzione Curve Turnings, cliccando con il tasto destro su qualsiasi nodo e selezionando l’opzione stessa.
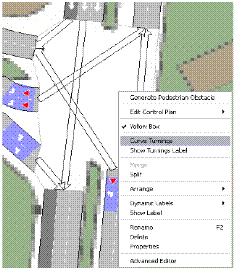
Figura 4.26
L’immagine seguente ci mostra il tipo di svolte create.
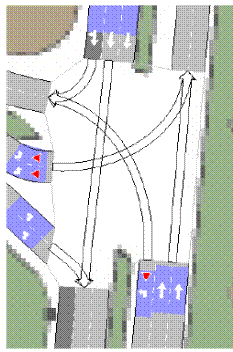
Figura 4.27
Nelle intersezioni, inoltre, è possibile modificare il punto in cui i veicoli aspettano di avere la precedenza. Ad esempio nella svolta a sinistra, rappresentata nella figura seguente, i veicoli provenienti da sud, non si fermano in corrispondenza del segnale, ma qualche metro più avanti.
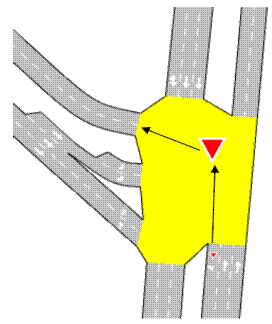
Figura 4.28
Per creare questo punto, occorre creare una linea di attesa in corrispondenza della svolta. Per fare ciò clicchiamo con il tasto destro sulla svolta e selezioniamo l’opzione Stop Lines/New.
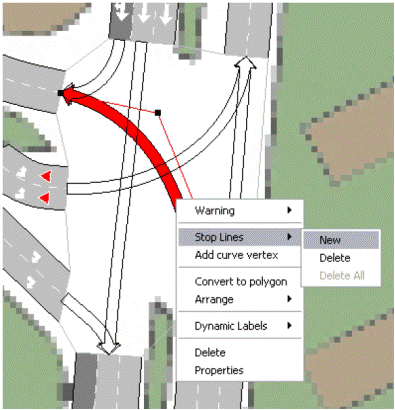
Figura 4.29
La linea di attesa può essere modificata spostandola con il mouse.
4.2.6 Assegnazione del tipo di strada alle sezioni
I tipi di strada che si possono assegnare alle sezioni sono mostrati nell’immagine seguente.
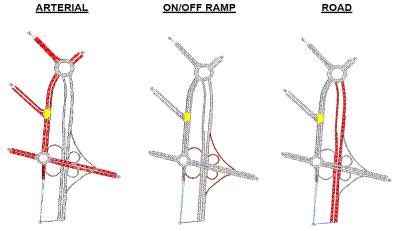
Figura 4.30
Da default tutte le sezioni sono di tipo Arterial. Si può cambiare la tipologia facendo doppio click nella finestra di progetto e selezionando la cartella ‘Road and Lane Types’, oppure premendo il tasto destro, una volta selezionata la sezione, e scegliendo l’opzione Road Type nel context menu che appare.
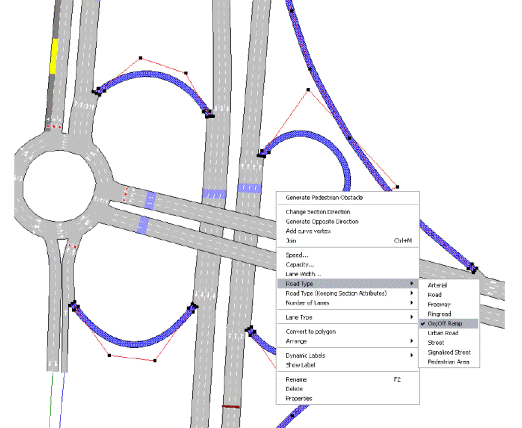
Figura 4.31
Al fine di rappresentare la domanda è necessario definire il Traffic State. La seguente figura fornisce tutte le informazioni necessarie per crearlo:
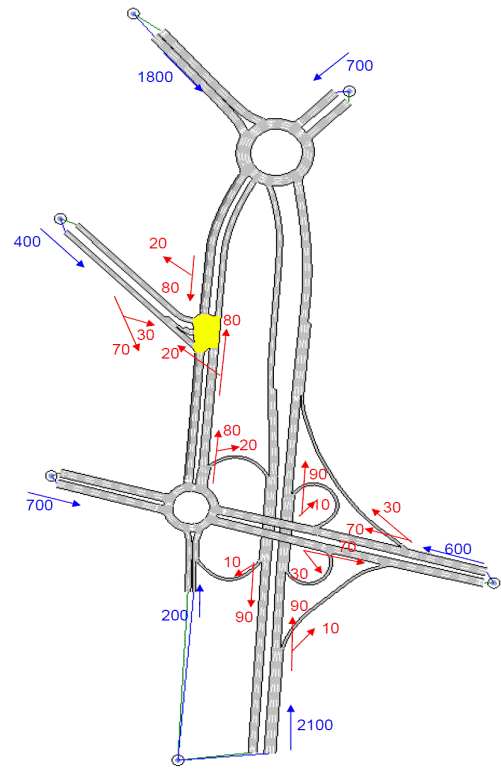
Figura 4.32
Per inserire tutti questi dati nel modello, è necessario creare un Traffic State dal menu Project/New/Demand Data/Traffic State.
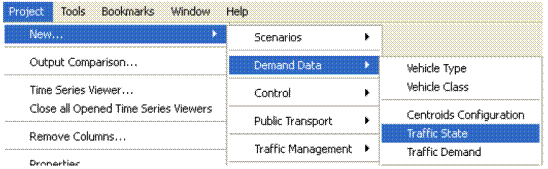
Figura 4.33
Apparirà nella Project Window una sottocartella denominata ‘Traffic State’ contenuta nella cartella ‘Demand Data’. È possibile rinominare la cartella, ad esempio ‘State Car: 08:00’, e, cliccando due volte, cambiarne i parametri come segue:
- associare al vehicle type la denominazione car;
- regolare il tempo d’inizio della domanda, ad esempio 08:00:00, e la sua durata, ad esempio 1h (01:00:00);
- selezionare l’opzione Show only Entrances;
- inserire nella colonna Flow i dati relativi all’immagine precedente, vale a dire i flussi di traffico.
Fatto ciò cliccare sulla tendina Turning Info e inserire le percentuali di svolta.
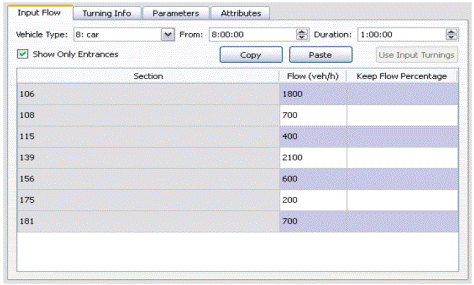
Figura 4.34
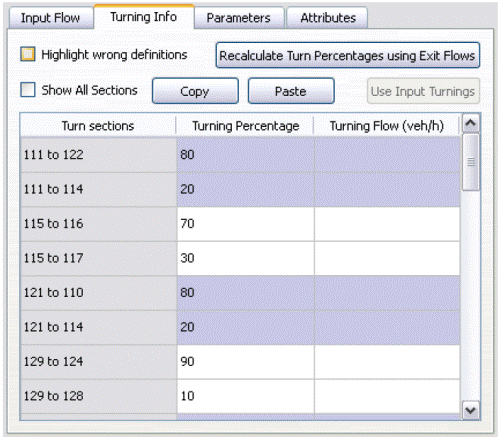
Figura 4.35
Se la domanda di traffico è data sotto forma di Matrice O/D, allora il primo passo consiste nel definire i centroidi ai quali è associata la matrice. Nel nostro esempio, i centroidi e le loro connessioni sono definiti come mostra la prossima figura.
Per posizionare un centroide sulla rete si deve prima
cliccare sull’icona 
e
successivamente sul punto della rete ove lo si vuole inserire.
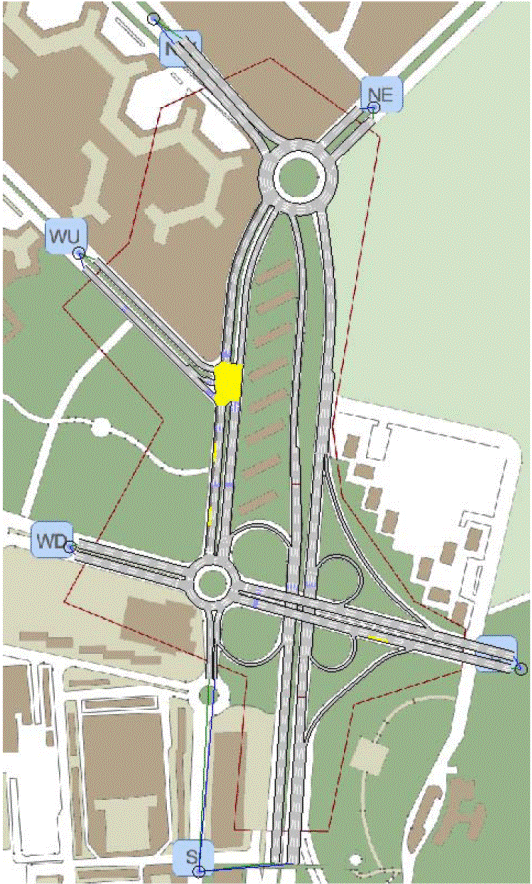
Figura 4.36
Dopo aver definito un centroide, basta cliccarvi sopra due volte e apparirà sul display l’editor del centroide, nella tendina ‘Main’ dell’editor è possibile cambiare il nome al centroide. Infine occorre connettere il centroide alla rete e viceversa, la rete al centroide. Ciò può essere fatto premendo New e selezionando la sezione di entrata o di uscita. Quando tutte le connessioni sono state fatte, premere OK.
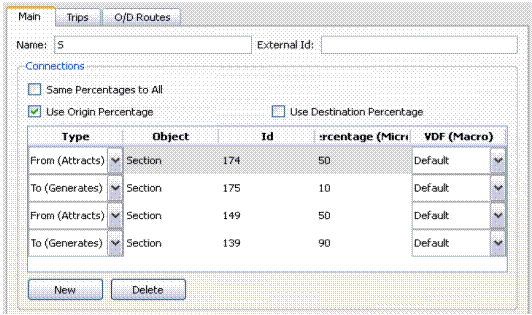
Figura 4.37
Creeremo la matrice OD partendo da una matrice totale dalla quale estrarremmo due matrici, una relativa alle auto, l’altra riferita ai mezzi pesanti. Considereremo che il 95% dei viaggi della matrice totale sono fatti da auto, mentre il restante 5% sono camion.
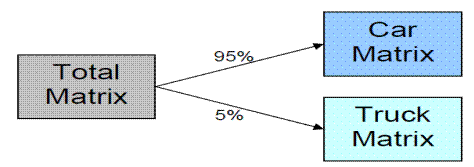
Figura 4.38
La matrice totale è la seguente:
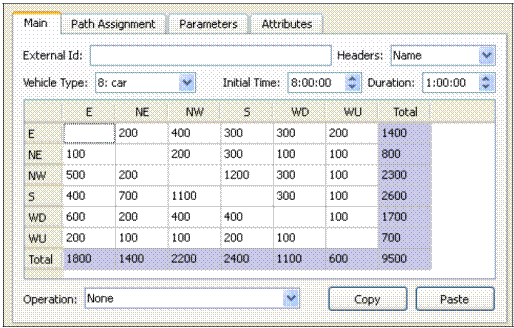
Figura 4.39
È possibile creare la matrice dalla cartella ‘Centroid Configuration’, posta nella Project window. Cliccando con il tasto destro del mouse sulla configurazione, si aprirà una tendina; selezionare l’opzione New/ O-D Matrix, rinominare la matrice come ‘Total Matrix’ e inserire i dati, cliccando due volte su di essa.
L’operazione successiva è quella di sdoppiare la Total Matrix in due sottomatrici, una delle auto e l’altra dei mezzi pesanti. Per fare ciò occorre:
- cliccare due volte su Total Matrix;
- selezionare l’opzione split all’interno della finestra di dialogo;
- premere due volte New per inserire le percentuali secondo le quali dividere la Total Matrix;
- selezionare Execute.
All’interno della finestra di progetto appariranno due nuove matrici. Aprendo ciascuna di esse è possibile cambiare il tipo di veicolo e modificarne il nome.
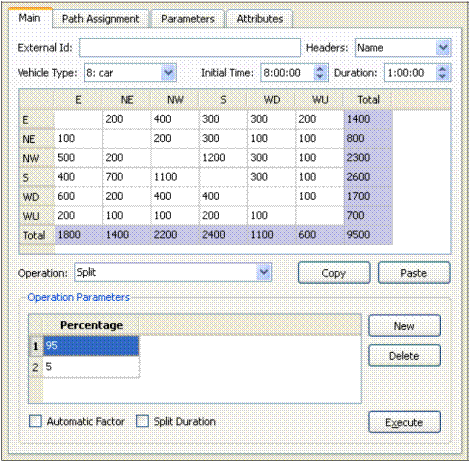
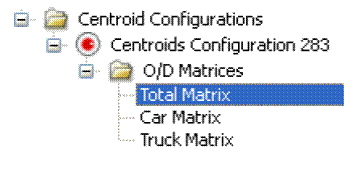
Figura 4.40
Ora che abbiamo costruito le matrici OD e il Traffic State, è possibile inserire due domande (Traffic Demands). Per fare ciò selezioniamo da menu Project / New / Demand Data / Traffic Demand; apparirà all’interno della Project Window una nuova voce Traffic Demand.
Figura 4.41
1) With OD Matrices
Rinominare il primo Traffic Demand come ‘Traffic Demand Matrix’, quindi cliccare due volte su di esso ed eseguire i seguenti passi:
- Indicare il tipo (Type): Matrices.
- Premere Add Demand Item ed inserire le matrici delle auto e dei mezzi pesanti, create nel paragrafo precedente.
- Premere Ok per terminare.
Figura 4.42
2) With Traffic States
Rinominare l’altra Traffic Demand come ‘Traffic Demand State’, quindi cliccare due volte su di essa ed eseguire le seguenti operazioni:
- Scegliere il tipo (Type): States.
- Premere Set Time e inserire Initial Time 8:00:00 e Duration 1:00:0.
- Premere Add Demand Item e inserire il Traffic State preparato nel paragrafo precedente.
Per avviare una simulazione è necessario creare uno scenario ed un esperimento. Costruiamo prima lo Scenario. Possiamo farlo andando su Project / New / Scenarios / Dynamic Scenario; apparirà la cartella ‘Scenarios’ all’interno della Project Window. È ora possibile creare un esperimento associato a questo scenario: clicchiamo con il tasto destro sulla cartella scenario, all’interno della finestra di progetto, quindi selezioniamo, dal context menu che apparirà, l’opzione New Experiment. All’interno della finestra di dialogo scegliamo il tipo di esperimento Aimsun Micro e Dynamic Traffic Assignment. È ora possibile aprire l’editor di scenario, cliccando due volte, e scegliere tra le due domande che abbiamo precedentemente creato.
Figura 4.43
Figura 4.44
Se vogliamo simulare lo scenario, dobbiamo costruire il comando replication. Occore pertanto cliccare con il destro su Experiment e andare su New/Replication come mostrato in figura:
Figura 4.45
Ora basta cliccare con il bottone destro su Replication e scegliere Animated Simulation; apparirà la finestra di dialogo della simulazione e saremo capaci di eseguirla cliccando sul tasto play.
Figura 4.46
[1] Microsimulator and Mesosimulator Aimsun 6.1 User’s Manual December 2010, 1997-2010 TSS-Transport Simulation Systems
[2] Aimsun 6.1 Usres Manual May 2010, 2005- 2010 TSS-Transport Simulation Systems
5.1 Il modello alla base di Tritone
TRITONE basa il suo funzionamento su modelli in grado di rappresentare singolarmente il movimento di ciascun veicolo in funzione del comportamento del conducente. Quest’ultimo segue le regole dettate dalla teoria dell’inseguitore (Car-Following), dalla teoria del cambio corsia (Lane-Changing), dalla logica dell’intervallo minimo di accesso (Gap-Acceptance) e dal sorpasso (Over-taking). In sostanza, i conducenti tendono a viaggiare con la velocità desiderata, ma l'ambiente circostante (i veicoli che precedono, i veicoli adiacenti, la geometria della strada, i segnali stradali ed i semafori, gli ostacoli, ecc.) condiziona il loro comportamento. Il tempo di simulazione è diviso in piccoli intervalli di tempo, chiamati cicli di simulazione oppure intervalli di simulazione (Δt); ad ogni ciclo, la posizione e la velocità di ciascun veicolo esaminato nel sistema, vengono aggiornate in accordo con
le leggi sopra indicate, di cui si fornisce, di seguito, una breve descrizione. L’aggressività e lo stile di guida dei conducenti possono influenzare l’andamento della simulazione, in quanto i guidatori “molto abili” o “aggressivi” hanno tempi di reazione più brevi degli altri; essi possono guidare vicino ai veicoli che li precedono, possono trovare intervalli di accesso più rapidamente e facilmente e possono accelerare e frenare repentinamente. I modelli implementati in TRITONE che descrivono la circolazione veicolare sono:
- Car-following
Ciascun conducente tende a raggiungere una velocità prescelta sulla base del suo stile di guida, delle prestazioni del veicolo che guida, e delle caratteristiche geometriche della strada che sta percorrendo; se durante la marcia raggiunge un veicolo che lo precede, dovrà rallentare ed adeguare la sua velocità o, se ciò non fosse possibile, cambiare corsia.
- Lane-changing
Ciascun conducente stabilisce, istante per istante, l’opportunità o meno della manovra di cambio corsia sulla base della necessità, della desiderabilità e dell’attuabilità della manovra.
- Over-taking
Ciascun conducente stabilisce, istante per istante, l’opportunità o meno della manovra di sorpasso sulla base della necessità, della desiderabilità e dell’attuabilità della manovra.
- Gap-acceptance
Ciascun conducente stabilisce quando eseguire una manovra (cambiare corsia, attraversare un’intersezione, inserirsi in un flusso di traffico, entrare in una rotatoria, ecc.) valutando se esiste l’intervallo temporale minimo necessario per la manovra, sulla base delle velocità relative degli altri veicoli.
Alcune funzioni di distribuzione, riguardanti le velocità e il distanziamento tra i veicoli, permettono di valutare il comportamento differente di diversi conducenti. La calibrazione del modello d'accodamento dei veicoli è stata fatta con l’aiuto di numerose sperimentazioni eseguite presso il Dipartimento di Pianificazione Territoriale dell’Universita della Calabria. Alcune recenti misurazioni garantiscono la modellizzazione corretta del comportamento, che si è evoluto nel tempo, e delle prestazioni tecniche più avanzate dei veicoli.
In TRITONE, la simulazione del comportamento di un conducente, su una carreggiata a più corsie, non tiene solamente conto dei due veicoli che lo precedono ma anche dei veicoli posti sulle corsie vicine. L’attenzione del conducente è influenzata, inoltre, dai semafori quando il veicolo arriva ad una distanza di circa 20 metri dalla linea d’arresto. Ogni conducente è assegnato, con i parametri che descrivono il suo comportamento, ad un veicolo preciso. Il comportamento del conducente si trova quindi in accordo con le prestazioni tecniche del veicolo. Le caratteristiche che determinano l’unità conducente-veicolo possono essere classificate in tre categorie:
1. Specifiche tecniche del veicolo:
ü lunghezza del veicolo
ü velocità massima
ü accelerazione
ü posizione istantanea del veicolo nella rete
ü velocità e accelerazione istantanea del veicolo
2. Comportamento dell’unità conducente-veicolo:
ü limiti psicofisici di percezione del conducente (capacità di stima, percezione della sicurezza, disposizione a correre dei rischi)
ü memoria del conducente
ü accelerazione in funzione della velocità attuale in rapporto alla velocità desiderata e al limite da normativa
3. Interazione tra più unità conducente-veicolo:
ü rapporti fra un determinato veicolo e i veicoli che lo precedono e che lo seguono nella stessa corsia e nelle corsie vicine
ü informazioni riguardanti l’arco di strada utilizzato
ü informazioni concernenti l’impianto semaforico più vicino.
Risulta evidente che l’utilizzo di un micro-simulatore comporta la necessità di descrivere in maniera approfondita e dettagliata tutte le informazioni relative alla domanda ed all’offerta, ma ciò non deve risultare un elemento scoraggiante; infatti si possono fare le seguenti considerazioni.
La domanda viene espressa attraverso una o più matrici O/D (ad es. una per il periodo della mattina, una per il periodo centrale della giornata e una terza per il periodo pomeridiano), una curva di distribuzione dei flussi nella giornata (facilmente ricavabile da un campione rappresentativo di rilevazioni continue di traffico), una descrizione della distribuzione tipologica del parco veicoli circolante (ad es. Fonte ACI più indagine a campione sulle percentuali di veicoli pesanti e commerciali), ed una stima della distribuzione tipologica dei conducenti (aggressività di guida, velocità massima, etc.). Tali informazioni sono ricavabili, attraverso l’applicazione di modelli di stima, da rilevazioni dei flussi di traffico condotte in particolari punti significativi della rete stradale.
Occorre evidenziare che il modello di micro-simulazione descrive, per sua natura in modo assai realistico, il comportamento dei veicoli e fornisce una descrizione decisamente attendibile della realtà, anche nel caso di stime indicative di alcuni dei parametri sopra descritti. L’offerta deve essere descritta in termini di geometria plano-altimetrica delle strade e delle intersezioni. Nella realtà, anche tale attività non risulta particolarmente onerosa; infatti, in Tritone, viene assai semplificata dalle procedure di disegno disponibili, in cui la rappresentazione parte da una descrizione schematica costituita da archi e nodi. Fornendo le sole indicazioni relative alla lunghezza della strada, al numero di corsie ed alla pendenza, la strada, nella sua complessità geometrica, viene disegnata automaticamente. All’utente rimane solo il compito di modificare eventuali condizioni particolari. Ulteriori rappresentazioni geometriche (raggi di curvatura, raccordi, ecc.) possono essere inseriti manualmente, al fine di migliorare la qualità della simulazione, di norma già comunque ottima anche in condizioni “standard”.
La micro-simulazione fornisce una visione dinamica del fenomeno in quanto, come accennato in precedenza, vengono prese in considerazione le caratteristiche del moto dei singoli veicoli (flusso, densità, velocità, etc.) non più medie, come accade nei macro-simulatori, bensì reali e variabili istante per istante durante tutta la simulazione. Attraverso la micro-simulazione è possibile rappresentare più famiglie di spostamenti, ognuna caratterizzata da differenti parametri comportamentali (accelerazione, decelerazione, aggressività, tempo di reazione, etc.) e da diverse tipologie di veicolo (velocità massima, dimensioni, prestazioni, parametri di emissione, etc.).
TRITONE è un modello di simulazione microscopica della circolazione. La circolazione viene simulata tenendo conto delle differenti caratteristiche riguardanti la struttura delle corsie, la composizione del traffico, la regolazione delle precedenze agli incroci e le prestazioni dei veicoli sia del traffico che del trasporto collettivo. Con TRITONE si possono valutare differenti modi di gestione del traffico attraverso la descrizione qualitativa e quantitativa della circolazione stessa. TRITONE può essere utilizzato per trovare soluzioni ad un gran numero di problemi. Alcuni esempi indicativi possono illustrare il vasto campo di possibilità di impiego di TRITONE:
- Con l’aiuto di TRITONE è possibile effettuare l’analisi della capacità e del funzionamento della circolazione;
- TRITONE permette di comparare tra di loro diversi scenari progettuali che includono incroci a precedenza regolata da segnaletica, incroci a rotatoria, incroci semaforizzati, incroci a livelli sfalsati. È possibile inoltre valutare la capacita della strada;
- TRITONE può essere utilizzato per valutare ed ottimizzare operazioni di traffico in reti complesse.
TRITONE offre la possibilità di riprodurre anche eventi di tipo eccezionale (cantieri, incidenti, emergenze, ecc.), utilizzando una rete viaria il più possibile corrispondente alla realtà (larghezza delle corsie, curvature dei tracciati, altimetrie, strettoie, ecc.). Ciò consente di ottenere risultati più che mai attendibili.
I molteplici strumenti di rappresentazione, offerti dal micro-simulatore, consentono di visualizzare e localizzare in modo semplice e veloce i punti critici che si formano sulla rete, determinare i tempi di attesa e le code ed individuare le possibili soluzioni ed i percorsi alternativi. A tal proposito è interessante sottolineare che, il comportamento dei conducenti può essere modificato, agendo su un parametro che
specifica il livello di aggressività. I risultati che fornisce il micro-simulatore sono molteplici e articolati; in particolare, i principali sono:
1. Informazioni sui singoli veicoli
ü numero e tipologia di veicoli circolanti sulla rete nel periodo di simulazione;
ü velocità media di ciascun veicolo;
ü ritardo medio;
ü distanza totale percorsa;
ü tempo di attesa in coda;
ü numero di sorpassi;
ü tempo totale di arresto.
2. Informazioni sui percorsi
ü tempo medio di viaggio.
3. Informazioni sui flussi veicolari e sulle criticità
ü istante di memorizzazione dei risultati;
ü flussi di manovra alle intersezioni selezionate;
ü indici di criticità.
4. Informazioni sugli incidenti
ü istante in cui si è verificato;
ü tratto di strada interessato;
ü durata dell’incidente;
ü lunghezza delle code.
5. Informazioni sui parametri ambientali
ü emissioni atmosferiche per singolo veicolo;
ü emissioni totali per sezione, per arco e per nodo;
ü indicatori di criticità ambientale.
6. Indicatori di Safety Performance
ü indicatori di criticità DRAC;
ü indicatori di criticità TTC;
ü indicatori di criticità PSD;
ü indicatori di criticità MADR.
7. Modelli implementati in Tritone
ü General Motors 3 Greemberg;
ü Giofré Modificato;
ü Giofré Primordiale;
ü Gipps (AIMSUN);
ü Van Aerde (Integration);
ü Yang (MITSIM);
ü FreSim and Intras;
ü Fritzsche (PARAMICS);
ü Wiedemann (VISSIM);
ü NETSIM;
ü CORSIM.
5.3 Organizzazione dell’area di lavoro
La schermata principale di TRITONE è molto semplice, essa è stata realizzata con il concetto di User Friendly, in alto si possono vedere tutti i comandi necessari alla simulazione, nell’area più grande la rete stradale e a destra il resoconto degli oggetti inseriti sulla rete. L’area di lavoro di TRITONE è organizzata principalmente in quattro categorie disposte nel seguente modo:
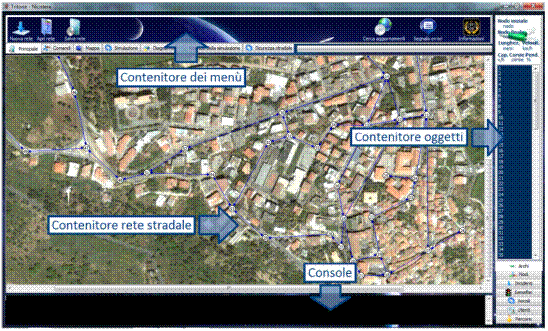
Figura 5.1: Schermata esemplificativa
Contenitore rete stradale.
Nel contenitore della rete stradale sono contenuti graficamente tutti gli oggetti come archi, nodi, semafori, edifici, segnali e veicoli, appartenenti alla rete stessa, compresa la mappa di sfondo.
Contenitore dei menu.
Nel contenitore di menu sono racchiusi quasi tutti i comandi di TRITONE. Esso è diviso in categorie di rapido accesso, con oggetti di grandi e semplici dimensioni per un più veloce utilizzo. E’ possibile individuare le seguenti categorie, la cui descrizione è contenuta in [1]:
Ø Categoria Principale
Ø Categoria Comandi
Ø Categoria Mappa
Ø Categoria Simulazione
Ø Categoria Diagrammi
Ø Categoria Risultati Simulazione
Ø Categoria Sicurezza Stradale
Ø Categoria Annotazioni
Contenitore oggetti
Nel contenitore degli oggetti vengono memorizzati tutti gli oggetti immessi manualmente o automaticamente sulla rete. Aprendo ognuna delle apposite sezioni è possibile, cliccando col puntatore del mouse su un oggetto della lista, visualizzare in alto le sue proprietà principali e, qualora esso fosse un oggetto fisico, vederlo selezionato anche nel contenitore della rete stradale. Cliccando invece col pulsante destro del mouse è possibile aprire un menu a tendina con le operazioni che si possono eseguire sull’oggetto, come eliminarlo, modificarne le caratteristiche o spostarlo.
Figura 5.2: Caratteristiche dell’oggetto
Console
TRITONE mette a disposizione anche una comoda console per immettere comandi più complessi relativi a combinazioni di comandi o a operazioni di dettaglio. In console è possibile visualizzare, inoltre, i risultati principali della simulazione nonché lo stato dell’attività del software. Facendo doppio click col puntatore del mouse su di essa, questa assume proporzioni doppie per consentire una più agevole lettura del contenuto.
Figura 5.3: Console
5.4 Creazione di una rete stradale
Per realizzare una nuova rete stradale basta cliccare sul pulsante “Nuova rete”, si aprirà una schermata di richiesta dati dove bisogna inserire il nome che si vuole dare alla rete, il progettista, il numero di incroci semaforizzati (è possibile introdurlo anche successivamente) e il numero di tipi di guidatori e di tipi di veicoli da simulare. Cliccando sul pulsante “Carica uno sfondo” è possibile caricare un’immagine di qualsiasi formato e dimensione come sfondo della rete (l’immagine deve essere situata nella stessa cartella in cui viene salvata la rete), cliccando invece su i due pulsanti di “Assegnazione Automatica”, sia per i tipi di utenti che per i tipi di veicoli, vengono assegnati automaticamente le rispettive tipologie standard presenti nel simulatore, mentre cliccando su “Conferma” si accede alla modalità di inserimento dei nodi sulla rete. L’area di lavoro diviene quindi bianca, se non viene caricata nessuna mappa di sfondo, e cliccando su questa e possibile inserire i nodi della rete. Si noti che non c’e distinzione fra nodi intermedi e centroidi.
5.4.1 Inserimento e modifica dei nodi della rete
La modalità di inserimento dei nodi sulla rete avviene automaticamente quando si crea una nuova rete, o può essere riattivata successivamente, mentre si è in altre modalità, mediante il pulsante “Modo ins. Nodi”, posto nella sezione dei comandi, figura 5.4.
Figura 5.4: Sezione dei comandi
Attivata la modalità, per inserire i nodi basta semplicemente cliccare col mouse sulla rete, nel contenitore della rete stradale, tenendo presente che non c’è distinzione fra
nodi intermedi e centroidi.
Figura 5.5: Inserimento nodi
Se la posizione del nodo non risulta essere corretta è possibile spostarsi nella sezione “Nodi” del contenitore degli oggetti, selezionare il nodo in esame e, cliccando col tasto destro del mouse, scegliere la voce “Sposta Nodo”. Apparirà quindi una nuova finestra che consente di spostare il nodo precedentemente inserito.
Per eliminare un nodo basta, invece, scegliere la voce “Elimina Nodo” tenendo presente che, se ad esso è collegato un arco, anche questo verrà eliminato.
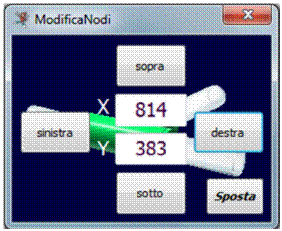
Figura 5.6: Finestra di dialogo Modifica Nodi
5.4.2 Inserimento e modifica degli archi della rete
Una volta terminato l’inserimento dei nodi è possibile passare agli archi cliccando sul pulsante “Modalità ins. Archi” nella sezione dei comandi, figura 5.7. Cliccando poi su una coppia di nodi, precedentemente disegnati, apparirà la finestra dove inserire le caratteristiche dell’arco, figura 5.8.
Figura 5.7: Sezione dei comandi
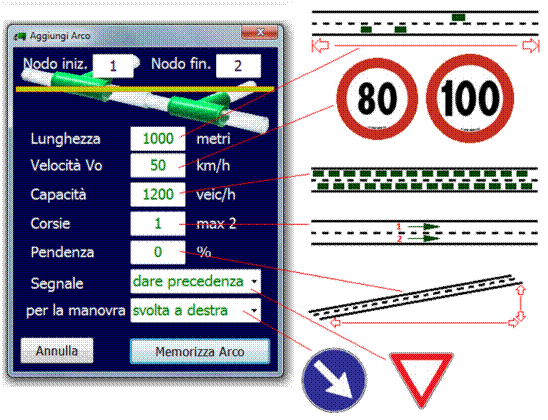
Figura 5.8: Finestra di dialogo relativa alle caratteristiche dell’arco
Per memorizzare l’arco premiamo sul pulsante “Memorizza arco”, quindi esso apparirà sia come oggetto sulla rete sia nella lista degli archi, nella sezione “Archi” del contenitore degli oggetti. Da notare che il verso dell’arco è identificato con un pallino blu se non è presente alcun segnale, arancione se è presente un segnale di dare precedenza, e rosso in caso stop.
Se alcune caratteristiche dell’arco devono essere modificate, è possibile spostarsi nella sezione “Archi” del contenitore degli oggetti, selezionare l’arco in esame e, cliccando col tasto destro del mouse, scegliere la voce “Modifica Arco”. Apparirà quindi una nuova finestra, dalla quale è possibile modificare le caratteristiche dell’arco precedentemente inserite. Per eliminare un arco basta, invece, scegliere la
voce “Elimina Arco”.
5.4.3 Inserimento e modifica dei flussi veicolari sulla rete
Una volta terminato l’inserimento degli archi è possibile passare ai flussi veicolari cliccando sul pulsante “Modalità ins. flussi” nella sezione dei comandi, quindi basta poi cliccare su una coppia di nodi per far apparire la finestra dove inserire la distribuzione di carico veicolare fra i due nodi, figura 5.9.
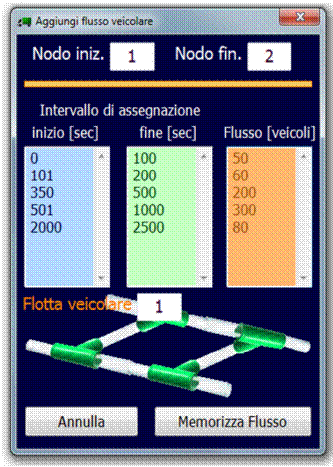
Figura 5.9: Finestra di dialogo relativa ai flussi
È possibile specificare sia una distribuzione continua che discontinua, evitando così di caricare periodi a flusso nullo, e la flotta veicolare che costituirà il flusso. Se alcune caratteristiche della corrente di traffico devono essere modificate, è possibile spostarsi nella sezione “Flussi veicolari” del contenitore degli oggetti, selezionare il flusso in esame e, cliccando col tasto destro del mouse, scegliere la voce “Modifica Flusso”. Apparirà quindi una nuova finestra da dove è possibile modificare le caratteristiche della corrente veicolare precedentemente inserita. Per eliminare una corrente veicolare basta invece scegliere la voce “Elimina Flusso”.
5.4.4 Inserimento e modifica incidenti o cantieri sulla rete
Con TRITONE è possibile simulare eventi temporanei, come la presenza di un cantiere o una situazione di incidente. Per fare ciò cliccare sul pulsante “Aggiungi interruzione” nella sezione dei comandi o, spostarsi nella sezione “Incidenti” del contenitore degli oggetti, ed, ivi cliccando col tasto destro del mouse nella lista, scegliere la voce “Aggiungi incidente o blocco”. La nuova finestra che apparirà, figura 5.10, consente di definire minuziosamente l’evento da simulare.
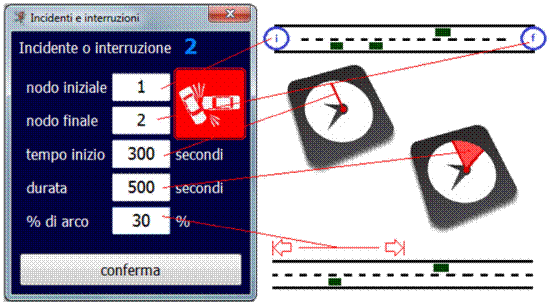
Figura 5.10: Finestra di dialogo relativa agli incidenti
Se alcune caratteristiche dell’evento devono essere modificate, è possibile spostarsi
nella sezione “Incidenti” del contenitore degli oggetti, selezionare l’evento in esame
e, cliccando col tasto destro del mouse, scegliere la voce “Modifica Incidente”. Apparirà quindi una nuova finestra da dove è possibile modificare le caratteristiche dell’evento precedentemente inserito. Per eliminare un evento basta invece scegliere la voce “Elimina Incidente”.
5.4.5 Inserimento e modifica dei semafori sulla rete
TRITONE consente di simulare la presenza di intersezioni semaforizzate, esprimendone il loro numero all’istante di creazione della rete, dalla finestra che appare quando si clicca sul pulsante “Nuova rete” o, dall’apposito pulsante “Agg. Semafor” nella sezione “Comandi”. Per inserire le lanterne semaforiche, una volta completata tutta la costruzione della rete, basta cliccare sul pulsante “Avvia sim.” nella sezione simulazione. La nuova finestra che apparirà consente di definire minuziosamente le fasi di ogni lanterna semaforica, inserendo prima la durata del ciclo semaforico e poi il numero di archi sul quale è posta una lanterna semaforica, figura 5.11, tenendo presente che se l’arco ha due corsie bisogna inserirne due di lanterne e non una.
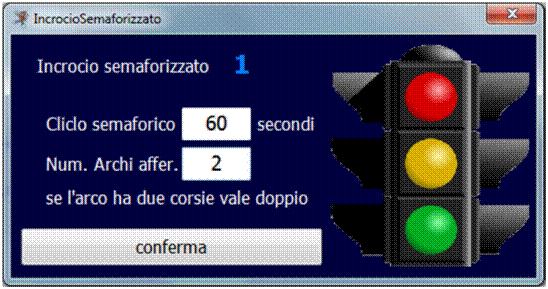
Figura 5.11: Finestra di dialogo relativa ai semafori
Clicchiamo su “Conferma” e inseriamo, di volta in volta, per ogni arco afferente all’incrocio semaforizzato in esame, le lunghezze delle fasi, il loro tipo, il nodo iniziale e quello finale dell’arco, la corsia dov’è posizionata la lanterna e il nodo di posizione della stessa, perché è possibile inserirla sia alla fine che all’inizio di un arco.
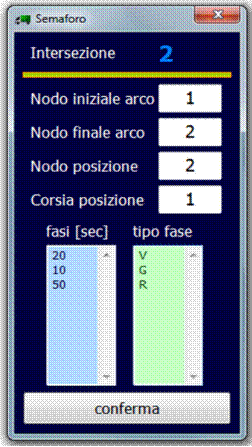
Figura 5.12: Fasi del semaforo
Occorre notare che il tipo di fase deve essere espresso semplicemente con la lettera iniziale del colore rappresentante, ovvero “V” o “v” per verde, “G” o “g” per giallo e “R” o “r” per il rosso. Nel caso in cui il conteggio dei tempi risulta errato, viene subito segnalato.
Se alcune caratteristiche della lanterna devono essere modificate, è possibile spostarsi nella sezione “Semafori” del contenitore degli oggetti, selezionare la lanterna semaforica in esame e, cliccando col tasto destro del mouse, scegliere la voce “Modifica Semaforo”. Non è possibile eliminare le lanterne semaforiche una volta inserite, perché esse fanno parte integrante della rete stradale computazionale.
5.5 Modifica dei parametri dei modelli
È possibile modificare i tempi di GAP/LAG e i vari parametri, utilizzati dai modelli
implementati in Tritone, mediante i comandi “Modifica GAP” e “Modifica par. modelli” nella sezione dei comandi. Nella finestra che apparirà si potranno modificare i vari parametri a proprio piacimento, considerando che per i modelli di car following, figura 5.13, la modifica avviene in dinamico, quindi se verranno modificati durante la simulazione, saranno subito utilizzati e si potranno apprezzare i cambiamenti di stato sul video.
Figura 5.13: Modifica dei parametri di Car-following
Ciò invece non avviene con i GAP e i LAG che devono essere modificati prima della simulazione.
I risultati delle simulazioni (per es. tempi di percorrenza, lunghezza delle code, emissioni di inquinanti, etc.) vengono restituiti sul display e possono essere trattati con le applicazioni Windows standard, come il blocco note o Excel. Gli output grafici, come l’animazione video, possono essere stampati utilizzando la funzione di
Stampa, la quale si trova tra gli appositi pulsanti disponibili nei menu. Le finestre e ogni altra visualizzazione in tempo reale, possono essere importate in applicazioni grafiche (Paintbrush, PaintShop Pro, Corel PhotoPaint) o in elaboratori di testi (Word, WordPerfect), utilizzando la funzione cattura a video di Windows o gli appositi comandi di TRITONE. È possibile raggiungere un miglior risultato impostando un’alta risoluzione del monitor.
Mettendo il segno di spunta su “Mostra controlli”, nella sezione simulazione, è possibile vedere gli effetti nel tempo del flusso veicolare sui singoli archi, in funzione dell’intervallo di controllo impostato. Verrà restituita una tabella avente le seguenti colonne:
- Δt: istante di conteggio [sec] (da notare che tutti i valori sono mediati nell’intervallo es. 120-240);
- NodoIn, NodoFn: nodi dell’arco;
- Lungh: lunghezza arco [m];
- V flib: velocità a flusso libero, o meglio il limite da normativa vigente sull’arco;
- V media: velocità media [km/h] sull’arco nell’intervallo Δt - Δt-1;
- V mcum: velocità media cumulativa nel tempo (tiene conto di tutti i veicoli fino a quel Δt);
- T flib: tempo a flusso libero [sec];
- T medio: tempo medio di percorrenza nell’intervallo (Δt – Δt-1);
- Veic U: veicoli usciti dall’arco;
- Veic T: veicoli transitati sull’arco nell’intervallo (Δt – Δt-1);
- Veic E: veicoli entranti nell’arco;
- Veic M: veicoli che ancora devono arrivare sull’arco in esame dall’assegnazione fatta;
- dens: densità media cumulativa nel tempo;
- Q port: portata veicolare (dens * V media) in [veic/h];
- CO2: emissioni;
- Con: consumo di carburante;
- P: peso medio sulla pavimentazione;
- Qt max: massimo numero di veicoli fisicamente osservati sull’arco nell’intervallo (Δt – Δt-1)
Terminata la simulazione è possibile visionare i risultati, tabellati e ordinati, mediante il pulsante “Vedi risultati ordinati” della sezione risultati della simulazione. Premendo questo tasto si aprirà una finestra contenente la tabella sopra citata.
Figura 5.14: Tabella dei risultati della simulazione
Nella finestra dei risultati si trovano due pulsanti che consentono di salvare la rete in formato semplice file di testo tabulato o, direttamente, nei nuovi formati di Microsoft Excel.
Altri risultati sono costituiti dai grafici; è possibile ottenerli semplicemente spuntando l’apposita casella relativa al grafico che si cerca, ad esempio i diagrammi del moto nel dominio spazio tempo. Tutti i diagrammi possono essere salvati come immagini tramite il pulsante “Salva Diagrammi” in formato PNG.
Altri output sono rappresentati dalla visualizzazione dei veicoli virtuali che si muovono sulla rete, nel caso bidimensionale.
I veicoli di colore rosso sono in decelerazione, quelli di colore arancione hanno accelerazioni basse o sono fermi, mentre quelli di colore verde hanno un’accelerazione normale. I semafori vengono rappresentati nel 2D come quadratini posti in prossimità dell’intersezione, nella propria corsia, a colore variante in funzione della fase. Alcuni veicoli possono però assumere colori diversi da quelli standard, ciò accade ad esempio quando sono in sorpasso; in tal caso diventano di colore fucsia. Se invece essi sono incidentati o rappresentano l’evento di un cantiere temporaneo, avranno colore blu.
[1] Tritone: Microsimulatore di reti stradali versione 10.9.1, La guida al simulatore stradale più semplice al mondo, realizzato da ing. Giofrè Vincenzo Pasquale presso Unical - Dipartimento di Pianificazione Territoriale.
