|
Ente |
Universita’ della Calabria |
|
Struttura |
Dipartimento di Ingegneria Civile |
|
Titolo |
Analisi della sicurezza stradale mediante la micro-simulazione degli incidenti nell’area di S.Anna (KR) |
|
Autore |
Lo Feudo Attilio |
|
Relatore |
Prof. Ing. Vittorio Astarita |
|
Correlatore |
Dott. Ing. Vincenzo Pasquale Giofrè |
|
Anno Accad. |
2018 - 2019 |
CAPITOLO 1 - Introduzione
Il presente lavoro di tesi si pone come obiettivo quello di valutare l’affidabilità di un nuovo software, Zombie Drive, per l’individuazione dei black-point sulle reti stradali in alternativa al classico Safety audit. L’algoritmo alla base del software si fonda sullo studio delle distrazioni dei conducenti e sugli effetti che esse hanno sulla sicurezza della circolazione. La maggior parte dei sinistri stradali infatti, al contrario di ciò che è usuale pensare, non sono da imputare a fattori di carattere ambientale, a problematiche di carattere ingegneristico come la cattiva progettazione dell’infrastruttura o l’inefficace manutenzione della pavimentazione stradale, bensì all’uomo ed al suo stile di guida. A riprova di ciò viene riportato in un comunicato stampa dell’ISTAT che le prime tre cause degli incidenti stradali, che nel 2017 in Italia hanno causato 3.378 morti, sono da ricercare tra i comportamenti errati da parte dei conducenti, tra i quali i più frequenti sono: la distrazione alla guida, il mancato rispetto delle regole di precedenza o del semaforo e la velocità troppo elevata. Nell’elaborato è stato effettuato un confronto sulle collisioni in funzione dell’energia d’ impatto e delle angolazioni di sbandamento sulla Statale 106 tra Steccato di Cutro (KR) e Crotone (KR) all’altezza della località Sant’Anna (KR). Il corretto funzionamento di un’infrastruttura di trasporto non dipende unicamente dalle leggi di afflusso/deflusso ma risulta influenzato dagli aspetti socioeconomici ed ambientali dell’area su cui essa viene riportata. Proprio in quest’ottica negli anni, molti filoni di ricerca si sono concentrati sullo sviluppo di sistemi di simulazione microscopica che hanno permesso di descrivere il moto dei singoli veicoli e di riprodurre le condizioni di esercizio della rete mediante la loro iterazione. In particolare, la simulazione del moto dei veicoli è un aspetto cruciale dei modelli microscopici che trovano i loro massimi campi di applicazione nel settore dell’ingegneria dove sono state messe a punto strutture che riproducono alcuni comportamenti propri della coppia veicolo-guidatore e che consentono di lavorare su posizione, velocità e accelerazione di ogni singola unità presente nella rete in un dato istante e appartenente ad un qualsiasi plotone di veicoli. Tuttavia, la problematica principale che ha alimentato i dibattiti scientifici riguarda il grado di accuratezza con cui i modelli microscopici di deflusso rappresentano il fenomeno reale in relazione allo scopo per cui possono essere utilizzati. Al di là di ciò, è possibile definire alcuni comportamenti di base che dovrebbero essere correttamente rappresentati per far sì che il modello sia sufficientemente coerente con la realtà. La corretta rappresentazione delle dinamiche di evoluzione dei veicoli e di conseguenza del traffico è tuttavia una problematica complessa. Il comportamento reale dei guidatori è molto eterogeneo e dipende non solo dall’ambito di guida, per esempio urbano o extra - urbano e dalla quantità di veicoli presenti, ma anche dalle caratteristiche dei soggetti umani. La disomogeneità di comportamento dei guidatori è inoltre alla base dei fenomeni di instabilità del deflusso veicolare verificabili nel sistema reale per valori della portata prossimi alla congestione dell’infrastruttura.
CAPITOLO 2 - Stato dell’arte
2.1 Sicurezza stradale
La sicurezza nel settore dei trasporti è un problema quanto mai 2018 a causa dei milioni di incidenti anche mortali che si verificano per le più disparate motivazioni. Essi hanno un costo sociale molto elevato basti pensare alle ricadute economiche sulla sanità pubblica ma anche e soprattutto sull’efficienza prestazionale dell’infrastruttura di trasporto in termini di tempi e deflusso. Proprio a causa di questi disagi l’aumento della sicurezza, intesa come rischio di incorrere in un incidente di gravità assegnata per unità di traffico, risulta un attributo da ricercare con perizia nell’ambito della progettazione. Nella pratica progettuale, il livello di sicurezza viene definito attraverso tre parametri principali:
· l’esposizione, che identifica le unità di traffico a rischio incidente,
· il rischio o tasso di incidentalità che individua la probabilità che avvenga un sinistro
· la gravità che rappresenta il livello di danno indotto dallo scontro (Progettare i Trasporti).
In generale, le più classiche metodologie per la limitazione dell’esposizione consentono di intervenire sui volumi di traffico, diminuendoli sensibilmente attraverso l’implementazione di sistemi integrati di trasporto collettivo, per definizione meno rischiosi. Altresì, è possibile procedere all’implementazione dei livelli di sicurezza attraverso l’incremento di due tipologie:
· Attiva, che riguarda errore umano, la velocità del veicolo, l’inadeguatezza dell’infrastruttura, il traffico.
· Passiva, che tiene conto delle condizioni al contorno.
In particolare, l’aumento della sicurezza attiva viene garantita attraverso l‘introduzione di dispositivi di bordo, ispezioni e manutenzione per quanto concerne il fattore di rischio legato al veicolo, attraverso l’applicazione da parte del conducente delle norme regolamentate dal codice della strada e attraverso specifiche di sicurezza riguardanti la geometria e l’impiantistica dell’infrastruttura. La resistenza passiva invece tiene conto dei dispositivi di protezione a bordo veicolo, quali cinture di sicurezza ed airbag, dei dispositivi di ritenuta posizionati e dei servizi di pronto intervento garantiti in prossimità dell’infrastruttura di riferimento. Come precedentemente affermato all’interno della breve introduzione, la maggior parte dei sinistri stradali sono imputabili a comportamenti scorretti da parte dell’automobilista ed in particolare alla distrazione. Considerando esclusivamente la distrazione alla guida, uno studio effettuato dall’Istituto Nazionale di Statistica, ha evidenziato che il numero di incidenti ad essa imputabili per l’anno 2017 è pari circa al 20% degli incidenti stradali con feriti. Dati pressoché simili sono stati rilevati negli Stati Uniti attraverso delle ricerche condotte da NHTSA (National Highway Traffic Safety Administration), da cui risultano che gli incidenti stradali dovuti alla guida distratta hanno causato 3.450 morti. Tuttavia, nonostante i dati allarmanti e le campagne d’ informazione e sensibilizzazione da parte degli organi statali, il fenomeno della distrazione continua ad essere sottovalutato da parte degli utenti. Ogni qualvolta un guidatore non presta attenzione, aumentano le probabilità che si verifichi un incidente stradale, con conseguenti rischi per il conducente, i passeggeri, i conducenti degli altri veicoli, i pedoni e le proprietà (Larson, Aaron, 18 July 2016). Scendendo più nel dettaglio, le distrazioni alla guida possono essere raggruppate in 3 categorie:
· manuali
· cognitive
· visive
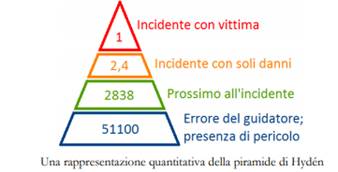
Si definiscono distrazioni manuali l’insieme delle azioni che portano il guidatore a rimuovere le mani dal volante, ad esempio mangiare/bere, fumare, cercare qualcosa nella borsa o nel portafoglio, sistemare la cintura di sicurezza del bambino, aggiustare lo specchietto retrovisore. Vengono definite invece distrazioni cognitive, l’insieme delle azioni comportano un abbassamento del livello di concentrazione o la perdita totale della stessa, essa può verificarsi in seguito all’assunzione di sostanze che alterano la normale capacità di intendere e volere dell’individuo ma anche semplicemente a causa della stanchezza. Infine, vengono definite distrazioni visive, quelle distrazioni che inducono il guidatore a distogliere, per un certo tempo, lo sguardo dalla strada: controllare e regolare il GPS, modificare la stazione radio, sistemare i controlli della temperatura, cercare oggetti sul pavimento della macchina e, infine, senza ombra di dubbio, la più diffusa e anche la più pericolosa, mandare/ricevere un messaggio di testo dal cellulare. Proprio questo fenomeno definito dagli addetti ai lavori come texting while driving risulta essere la prima causa di incidente nelle strade secondarie a causa della distorta valutazione delle diverse situazioni che si verificano durante il moto a partire dalla distanza di sicurezza. L’ analisi effettuata in comunione tra ACI e Polizia Stradale rivela gli effetti che l’invio di un sms genera sulla distrazione, in particolare l’invio di un messaggio che richiede un tempo di circa 10 secondi ad una velocità di crociera di 100 Km/h fa si che il veicolo percorra 300 metri senza nessun controllo da parte del guidatore. Negli ultimi anni i ricercatori di tutto il mondo si sono interrogati su quali azioni fossero le più pericolose per la sicurezza del guidatore e dei soggetti esterni, riuscendo nel 2016 grazie all’operato dei ricercatori del Virginia Tech Transportation Institute a catalogarle in base al potenziale rischio. Lo studio, pubblicato sul Proceeding of the National Academy of Sciences, è stato effettuato osservando il comportamento di circa 3500 guidatori volontari, di età compresa tra i 16 e i 98 anni di età, per più di 50 milioni di chilometri, per un periodo di 3 anni, in 6 differenti località degli USA. I veicoli esaminati sono stati preventivamente equipaggiati con telecamere, sensori e radar i quali rilevavano automaticamente: velocità, tempo di collisione, globale posizione del sistema di posizionamento (GPS), accelerazione e, tramite un software sviluppato nel corso dello studio, anche il comportamento oculistico del guidatore. L’esito dello studio, ha evidenziato che il rischio di incidente si è spostato bruscamente negli ultimi anni verso fattori legati al guidatore ed in particolare all’utilizzo di dispositivi elettronici portatili. Fattori legati ai guasti dei veicoli, alla progettazione o allo stato della carreggiata e alle condizioni ambientali incidono in percentuali complessivamente molto basse nel rischio incidenti. Vista l’importanza e soprattutto la gravità degli effetti derivanti dalla distrazione alla guida, i ricercatori americani del MIT AgeLab (Massachusetts Institute of Technology) e del Touchstone Evaluations, un’azienda di ingegneria dei fattori umani con sede nel Michigan, come riportato nell’articolo (To end distracted driving, MIT figures out how people really drive), si stanno concentrando sulle azioni e sui comportamenti di chi è al volante per massimizzare la sicurezza. Finanziati da importanti operatori di auto e tecnologia come Denso, Honda, Jaguar Land Rover, Google e Panasonic, i ricercatori stanno lavorando per registrare accuratamente l’azione degli esseri umani all’interno delle auto e modellare il loro comportamento. Nel 2009 il team ha fornito dei primi risultati circa la “consapevolezza dell’attenzione umana”, in termini matematici; si tratta di un algoritmo, definito AttenD, che prevedere, in presenza di arresti anomali, lo studio del comportamento dei singoli conducenti nei 20 secondi precedenti all’arresto. Questo tipo di ricerca potrebbe essere molto utile per costruire e testare prodotti sicuri, che installati sulle autovetture, sono capaci di aiutare attivamente nella guida. Ad esempio, in caso di incrocio sopraggiungente, l’auto potrebbe “oscurare” i display per evidenziare solo l’approccio con la strada mentre eventuali interazioni di smartphone o altri sistemi di bordo verrebbero posticipati soltanto dopo aver affrontato il momento in cui serve la massima attenzione. Come afferma Patton, capo ingegnere Denso, “l’idea è quella di avere a bordo, in futuro, prodotti o sistemi anti-distrazione della massima efficienza, in grado di adattarsi alle diverse problematiche di chi si trova al volante (adolescenti, anziani, soggetti a rischio di crisi cardiocircolatorie)”. In particolare, come riportato nello studio, questo tipo di ricerca diventa tanto più importante quanto maggiore è il numero di veicoli con funzioni automatizzate; automobili come Tesla, Mercedes-Benz, Audi e General Motors già o presto offriranno veicoli con funzionalità parzialmente automatizzate che gestiscono la guida. Bisogna tenere presente, tuttavia, che anche in queste auto i conducenti restano vitali per l’equilibrio di attenzione-sicurezza, è necessario che essi sappiano quando è il momento di riprendere il controllo manuale dai sistemi robotizzati. Anche questo significa conservare l’attenzione alla guida. Oggigiorno, ad esempio, i produttori di automobili mirano a sviluppare veicoli intelligenti con sistemi avanzati di assistenza alla guida (ADAS), che aiutano a ridurre gli errori del conducente. Una delle principali categorie di ADAS è legata ai sistemi anticollisione (CAS), congegnati in modo tale da avvisare il conducente, nei tempi necessari, di una reazione immediata e soprattutto adeguata per evitare una collisione. Come meglio esposto di seguito, i criteri adottati per definire tali sistemi sono basati sulle misure di sicurezza surrogata (SSM), ossia su indicatori di manovre evasive che, se opportunamente definiti, permettono di rilevare situazioni pericolose. Fino ad ora sono stati sviluppati, sulla base delle caratteristiche di movimento dei veicoli, diversi indicatori di sicurezza, la maggior parte dei quali si riferisce a collisioni a posteriori (Journal of Traffic and Transportation Engineering).Negli anni si è potuto osservare, infatti, che lo studio del comportamento conflittuale è un candidato naturale a tale scopo: i processi che provocano incidenti o conflitti di traffico, infatti, hanno molto in comune con i processi che precedono le collisioni reali (Hydén, 1987), tranne il risultato finale che è diverso (PNAS Proceeding of the National Academy of Sciences of the United States of America).Esistono tecniche per prevedere gli incidenti mediante la tecnica dei conflitti collegata alla capacità di registrare situazione prossimi all'incidente tra due componenti di traffico potenzialmente in conflitto ma che non si sono trasformati in veri e propri incidenti. Tale approccio consente di ampliare il campione di analisi su un sito specifico poiché non necessita direttamente dell'osservazione dell'incidente. In tal modo è possibile disporre della maggior frequenza dei conflitti rispetto agli incidenti, così come graficamente rappresentato dalla piramide di Hyden.
Nell’ambito dello studio di scenari virtuali si nota che molti modelli di simulazione del traffico commerciale non riproducono esplicitamente le misure di sicurezza del traffico e che le valutazioni di sicurezza devono essere effettuate estraendo le traiettorie dei singoli veicoli e post-elaborandole. Uno strumento comune utilizzato per eseguire questa operazione è il software SSAM. Il software SSAM sviluppato da FHWA nel 2008 è stato creato per la valutazione delle misure di sicurezza surrogate. Esso attraverso l'analisi delle traiettorie dei veicoli simulati, consente la valutazione di alcuni indici di sicurezza come TTC, PET e potenziali collisioni.
Time to Collision (TTC): Tempo che nelle diverse fasi del conflitto occorrerebbe ad un veicolo per scontrarsi con l'altro utente della strada se fosse mantenuta la velocità relativa corrente al punto dato. Il valore limite del TTC é stato definito nel 1991 da Van der Horst ed è pari A 1,5 secondi
Post Encroachment Time (PET): Periodo di tempo dal momento in cui il primo utente della strada sta lasciando la zona di conflitto fino a che il secondo utente non la raggiunga. Questo intervallo di tempo è proporzionale all’insicurezza della situazione di traffico osservata. PET risulta efficace sotto il profilo delle risorse in gioco ma si pone come alternativa meno dettagliata e più circoscritta rispetto al TTC.
CAPITOLO 3 – Metodologia
3.1 Software SSAM: generalità
La Federal Highway Administration ha sviluppato e messo a disposizione il software SSAM (Surrogate Safety Assessment Model- Modello di Valutazione della Sicurezza Surrogata), attraverso il quale si propone di offrire ai progettisti, ai ricercatori e alle aziende specializzate in progettazione e costruzione stradali, uno strumento per valutare la sicurezza di un’intersezione mediante la stima della frequenza dei conflitti. Il software elabora i file di traiettoria ottenuti in uscita da un programma di modellazione, come Aimsun™ (Gipps 1981), VISSIM™ (Wiedemann 1974, 1991), TEXAS™ o Paramics™ (Fritzsche and Ag 1994), valuta ogni singola interazione veicolo-veicolo e riesce a stabilire la presenza di un punto di conflitto e a catalogarlo. Al termine delle elaborazioni, SSAM presenta i risultati in tabelle permettendo all’utente di filtrarli secondo parametri di sua scelta. Il processo di elaborazione è schematizzato nella figura seguente:

Procedimento operativo di SSAM
I parametri più importanti per l’elaborazione sono:
· TTC (Time to collision) Tempo alla collisione;
· PET (Post Encroachment Time) Tempo successivo all’invasione di corsia.
· DELTA S
· CONFLITTI
3.1.1 TTC: Time to Collision
Uno tra i principali problemi della sicurezza stradale, sono gli scontri per tamponamento fra veicoli. Durante gli ultimi 10 anni sono stati introdotti, per migliorare la sicurezza stradale, sistemi ACAS (Advance Collision Avoidance System)., che mirano ad aiutare i conducenti nell’evitare gli incidenti avvisandoli di un potenziale scontro e, a volte, intraprendendo una frenata. Il tempo alla collisione (TTC), cioè “il tempo che occorrerebbe ad un veicolo che segue per scontrarsi con quello che lo precede, se fosse mantenuta la velocità relativa corrente al punto dato”, è stato stabilito come parametro potenziale per misurare la soglia temporale. Il primo ad introdurne la definizione originale fu Hayward, nel 1972, (Hayward 1972), sebbene ci fossero ricerche molto simili nei vari team di ricerca contemporanei. Secondo Hayward, nel momento in cui è in corso uno scontro, il valore di TTC diventa finito e diminuisce con il tempo, la misura critica nella valutazione della severità di conflitto diventa, a questo punto, il minimo valore di TTC durante il conflitto. Quindi, il valore massimo è infinito ed il minimo è pari a zero, ovvero l’incidente. Gli studi basati sull’utilizzo del Time-to-Collision (TTC), fanno riferimento ad un livello di soglia limite al fine di determinare la distinzione tra eventi critici gravi o rilevanti per la sicurezza e gli eventi trascurabili. La soglia limite è rappresentata da un valore fisso piuttosto che da una funzione che dipenda da una misura relativa alla velocità o alla decelerazione. Van der Horst e Farber (Van der Horst and Kraay 1986, Farber 1991) hanno suggerito, per distinguere fra situazioni sicure e non, un valore di TTC di 4 secondi. Tuttavia, Nilsson (Nilsson 1989) ha prodotto valutazioni soggettive che indicano che una soglia di 4 sec può essere "troppo breve", riportando un esperimento per confrontare tre meccanismi di evasione dalla collisione su test basati sul criterio di TTC in relazioni a manovre intraprese dal veicolo. Hirst e Graham (Hirst S. e Graham 1997) hanno riscontrato che un valore di TTC di 3 secondi risulta ancora inadatto in situazioni critiche, anche se, hanno ridotto il numero dei cosiddetti “falsi allarmi” o falsi conflitti. Hogema e Janssen (Hogema, J.H., Janssen, W.H., Coemet, M. e Soeteman 1996) hanno studiato i comportamenti dei guidatori durante l’approccio ad una situazione di coda con e senza guida assistita, sostenendo l’esperimento con un simulatore di movimento. È stato determinato un valore minimo di TTC pari a 3.5 secondi per i conducenti non supportati da guida assistita e 2.6 secondi per gli altri. Uno studio effettuato da Van der Horst (Van der Horst and Kraay 1986) utilizzando registrazioni video di situazioni di conflitto in tempo reale, ha suggerito un TTC di 4 secondi come soglia tra situazioni dove gli utenti si trovano in situazioni pericolose. Maretzke e Jacob (Maretzke, J e Jacob 1992) hanno sostenuto che i guidatori tendono a frenare a circa quattro secondi, il che non fornisce abbastanza tempo di reazione, quindi hanno suggerito una soglia di 5 secondi. È stata riscontrata una diminuzione nei valori assoluti per il TTC minimo con la diminuzione nella velocità. Il Tempo a collisione (TTC) è definito da Cavallo e da Laurent (Cavallo, V e Laurent 1988) come "il tempo che occorrerà per raggiungere un ostacolo" ed è un indicatore previsionale cruciale nella regolazione della frenata.
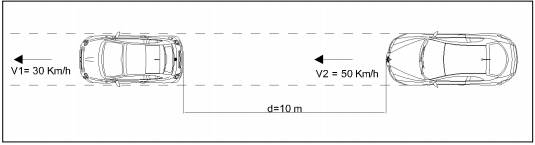
Fig. 3.1.1.1. Esempio di calcolo TTC
Il TTC comprende due fattori principali nel comportamento del conducente, la velocità relativa (∆V) e la distanza relativa (∆X) rispetto alla posizione del primo utente. Tuttavia il TTC, non considera che occorre una distanza d’arresto maggiore per velocità più alte e così può risultare inadeguato l'uso di una soglia costante di TTC per distinguere fra le situazioni sicure e quelle pericolose. Nelle figure successive è riportato un esempio che rappresenta una situazione tipica di conflitto ed il calcolo del TTC. Le figure mostrano (Fig. 3.1.1.2., 3.1.1.3.) il calcolo di TTC in due occasioni separate in funzione della distanza tra il veicolo uno e la zona di conflitto, anche se si deve notare che questi calcoli sono effettuati a intervalli di tempo continui durante il corso di un evento critico allo scopo di determinare il valore minimo di TTC

Fig. 3.1.1.2. Esempio di una situazione di conflitto e calcolo del TTC
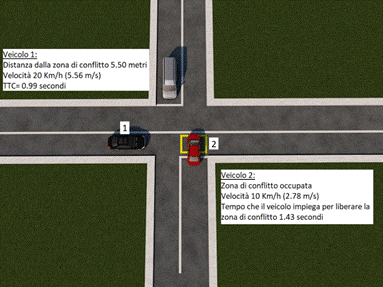
Fig. 3.1.1.3. Esempio di una situazione di conflitto e calcolo del TTC (fonte SSAM)
E’ possibile notare che il valore del TTC, calcolato per due istanti di tempo differenti e quindi per due diverse distanze dalla zona di conflitto, è minore del tempo che impiega il veicolo 2 a liberare la zona di conflitto. Risulta quindi impossibile evitare un incidente tra i due veicoli.
3.1.1.1 Vantaggi e svantaggi del TTC
Nel caso in cui il veicolo leader (che precede) è leggermente più veloce di quello following (che segue), l'indice TTC non può essere valutato in un numero finito. Questo è un punto debole dell’aspetto pratico dell'indice. In uno studio sui conflitti dovuti al cambiamento di corsia di un utente (leader) sulla corsia di sorpasso si è trovato che la velocità media di un secondo veicolo (following) che percorre la corsia di sorpasso, è leggermente inferiore a quella del veicolo leader. Quindi, è difficile valutare l'indice TTC fra il veicolo che cambia corsia ed il veicolo che percorre la traiettoria lungo la corsia di sorpasso. Tuttavia, la situazione dove la distanza fra due veicoli successivi è molto corta dovrebbe essere considerata una situazione pericolosa, anche se il veicolo leader viaggia leggermente più veloce dell’altro veicolo. In tali situazioni, vi è un'alta possibilità che il veicolo leader (che precede) venga tamponato nel caso in cui applica una frenata d’emergenza. Quindi vi sono casi in cui l'indicatore indica una condizione sicura anche se questa può risultare abbastanza pericolosa se non vengono considerati alcuni parametri. In tali casi, ci sono ancora aspetti da sviluppare per rendere gli indicatori di conflitto adeguati all’analisi di sicurezza. Sono diverse le situazioni che non sono interpretabili con il TTC. Uno studio svedese, presentato da Jeffery Archer (Archer 2005b, 2005a), rappresenta una valutazione di sicurezza basata sugli indicatori prossimali differenti di sicurezza in corrispondenza di intersezione a T a tre bracci nell'ambiente urbano e suburbano di Stoccolma. Gli indicatori di sicurezza esaminati includono il TA, il TTC e il PET. La manovra di svolta dalla strada secondaria risulta essere la causa di un gran numero di conflitti per cui risulta valutabile il TTC. Questi risultati danno risalto ai problemi relativi alle manovre di immissione da sinistra e di svolta a destra. L'indicatore TTC ha identificato alla stessa maniera un gran numero di conflitti per tamponamento così come un gran numero di eventi critici fra i veicoli ed i pedoni alle due intersezioni urbane oggetto dello studio. Le frequenze del TTC sembrano seguire un modello che è costante con le variazioni di volume relative al traffico. Il tentativo di affiancare il tasso di frenata al grado severità del TTC per intersezioni differenti evidenzia alcune differenze. È interessante notare che i valori di severità del tasso di frenata sono considerevolmente più piccoli di quelli per i conflitti seri, suggerendo che un certo numero di eventi registrati potrebbero non essere tanto seri come indica il TTC. In conclusione, l'indicatore di sicurezza TTC è una risorsa che richiede un calcolo considerevole per ogni evento critico potenziale. Esso, sicuramente trarrebbe giovamento da una procedura completamente automatizzata di analisi video.
3.1.2 PET
Il PET, acronimo di “post encroachment time”, è definito come “il periodo di tempo conteggiato dal momento in cui il primo utente della strada lascia la zona di conflitto fino all’arrivo del secondo utente nella medesima area”. Questo intervallo di tempo è proporzionale all’insicurezza della situazione di traffico osservata. Occorre fare una precisazione: il calcolo di TTC necessita della presenza di uno scontro in corso, ovvero gli utenti coinvolti dovranno essere nello stesso posto allo stesso tempo, nel caso mantenessero invariate traiettoria e velocità. Se gli utenti della strada si mancano per un piccolo intervallo di tempo (ad esempio nel caso di intersezione tra le traiettorie), non si può calcolare TTC, anche se la situazione non può essere considerata sicura. Questa insufficienza viene compensata con il Post Encroachment Time (PET). Fu Allen (Allen, B.L., Shin, B.T. e Cooper 1978) a proporre come indicatore il PET. La posizione occupata dal primo veicolo è definita come l’area di conflitto in cui con ogni probabilità avverrà lo scontro, quindi l'indicatore è definito come il tempo dal momento iniziale del conflitto al momento nel quale il secondo veicolo raggiunge l’area suddetta. Infatti, se nell'intersezione delle traiettorie previste, i due veicoli non arrivano a scontrarsi, il TTC non è calcolabile. Tuttavia, se la differenza di tempo fra due veicoli è piccola anche se non si scontrano, il valore potrebbe essere utile per l’analisi di sicurezza. Questa differenza di tempo è calcolata come PET
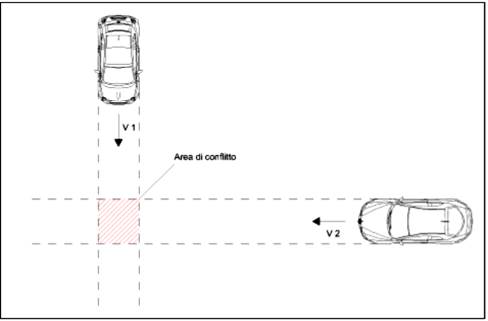
Fig. 3.1.2.1. Individuazione area di conflitto.

Fig. 3.1.2.2. Esempio di una situazione di conflitto
Di seguito viene riportato un esempio del calcolo del Post Encroachment Time (PET) in cui due veicoli sono coinvolti in un evento critico.
Nella figura vengono evidenziate le condizioni del conflitto per l’inizio e la fine del calcolo del PET.
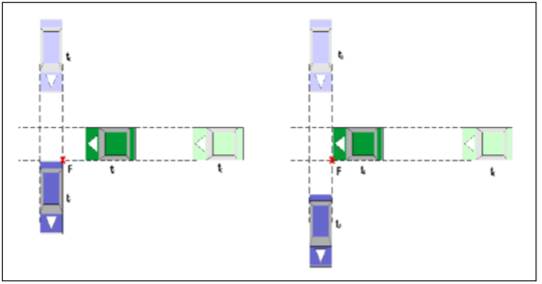
Fig. 3.1.2.3. Definizione di PET
t0: momento reale, T1: il primo utente della strada lascerà la zona di conflitto, T2: il secondo utente della strada raggiungerà la zona di conflitto, PET = T2-T1.
3.1.2.1 Vantaggi e svantaggi del PET
È lo studio del Jeffery Archer (Archer 2005b, 2005a) il documento di riferimento che spiega le limitazioni e le potenzialità del PET. Il PET è un indicatore utile per valutare situazioni in cui lo scontro viene mancato per poco. Tuttavia, non viene rappresentata come pericolosa una situazione che vede entrambi i veicoli procedere paralleli con distanze ravvicinate. Entrambi gli indicatori (TTC e PET) considerano "soltanto" se uno scontro accade, non considerando l'intensità necessaria di un'azione evasiva per evitare l’incidente. Durante una situazione di traffico sarà calcolabile sia il TTC che il PET in un determinato istante. Così facendo, si potrebbe ottenere una misurazione continua della sicurezza durante l’intero svolgersi della situazione di traffico, colmando le lacune dei singoli indicatori. Il PET non è utile per traiettorie longitudinali di conflitto ed è più utile per gli eventi critici di sicurezza che vedono le partecipazioni di veicoli e con utenti più vulnerabili (quali pedoni e ciclisti) e per determinate tipologie di interazioni veicolo-veicolo. Data la natura elementare di questo indicatore di sicurezza e la facilità relativa con cui i valori possono essere determinati usando l'analisi video, il PET risulta efficace sotto il profilo delle risorse in gioco ma si pone come alternativa meno dettagliata e più circoscritta rispetto al TTC.
3.1.3 Delta S
Differenza di velocità tra due veicoli, osservata a tMinTTC. Più precisamente, questo valore è matematicamente definito come la differenza di velocità dei veicoli (o traiettorie), tale che se v1 e v2 sono i vettori di velocità rispettivamente del primo e del secondo veicolo, allora DeltaS = || v1 - v2 ||. Si consideri un caso in cui entrambi i veicoli viaggiano alla stessa velocità, v. Se viaggiano nella stessa direzione, DeltaS = 0. Se le loro traiettorie tracciano un percorso perpendicolare, DeltaS = (√2) v. Se si stanno avvicinando DeltaS = 2v.
3.1.4 ConflictType
Classifica se il conflitto è un conflitto sulla stessa corsia, di cambio di corsia o di attraversamento o invasione corsia. Se le informazioni di collegamento e corsia non sono disponibili per entrambi i veicoli, il tipo di evento viene classificato in base al valore assoluto dell’angolo di conflitto come segue: conflitto sulla stessa corsia se ||ConflictAngle||<30°, conflitto di attraversamento se ||ConflictAngle ||> 85°, altrimenti conflitto di cambio corsia. Tuttavia, il modello di simulazione che ha prodotto i dati della traiettoria del veicolo può generalmente fornire informazioni di collegamento e corsia per entrambi i veicoli, anche se la codifica di questi valori può variare significativamente tra i vari software di micro-simulazione. Se sono disponibili informazioni di collegamento e corsia, tali informazioni vengono utilizzate per la classificazione nel caso in cui i veicoli occupino entrambi la stessa corsia all'inizio o alla fine del conflitto. Se i veicoli occupano entrambi la stessa corsia all'inizio e alla fine dell'evento, vengono classificati come conflitti sulla stessa corsia. Se uno dei due veicoli termina il conflitto in una corsia diversa da quella iniziata (pur non avendo cambiato i collegamenti), allora il conflitto è classificato come cambio corsia.
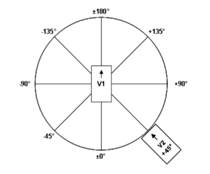
Fig. 3.1.4.1. Angolo di conflitto (fonte: report FHWA (Gettman et al. 2008))
3.2 Zombie Driver
Zombie Driver (Astarita and Giofré 2018) valuta le collisioni mediante il calcolo dell’energia dovuto a tre tipi di eventi che si generano a causa di un evento di distrazione. Questo evento suppone che il veicolo prosegua su una traiettoria alterata da un angolo che varia in tre modi 0°, +15°, -15°. In queste condizioni il guidatore distratto mantiene la velocità che aveva al momento dell’inizio della fase di distrazione. I tre tipi di eventi sono la collisione tra veicoli, tra veicoli e oggetti elastici, come le barriere e tra veicoli e oggetti rigidi come alberi o muri. Ciò che varia nei tre casi è solo l’equazione per il calcolo dell’energia generata durante l’impatto.
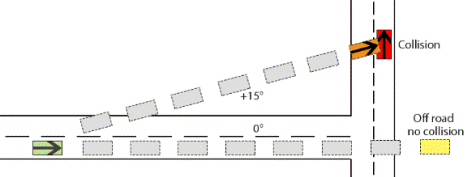
Fig. 3.2.1. ( Zombie Driver - Transport Innovation Software)
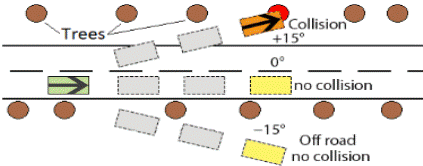
Fig. 3.2.2. ( Zombie Driver - Transport Innovation Software)
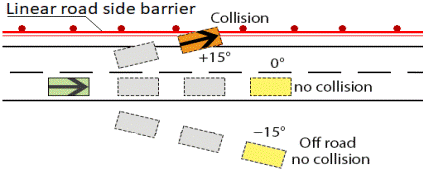
Fig. 3.2.3. ( Zombie Driver - Transport Innovation Software)
Ogni stante di distrazione viene calcolata l’ipotetica distanza percorsa e lo scostamento delle nuove relative coordinate rispetto le precedenti, con le equazioni:
DistanzaPrevista =![]()
𝑑𝑥 =
DistanzaPrevista ∗ Cos(Veicolo![]() +
Angolo.Alterazione)
+
Angolo.Alterazione)
𝑑𝑦 =
DistanzaPrevista ∗ Sin(Veicolo![]() +
Angolo.Alterazione)
+
Angolo.Alterazione)
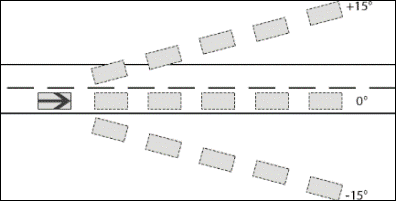
Fig. 3.2.4. ( Zombie Driver - Transport Innovation Software)
Ogni veicolo o oggetto è identificato sull’area attraverso le coordinate, in metri, dei quattro spigoli che formano il rettangolo. Successivamente viene valutata una eventuale collisione tra il veicolo in esame e un altro veicolo/oggetto rigido/oggetto elastico, attraverso l’intersezione delle rette che compongono i lati dei rettangoli.
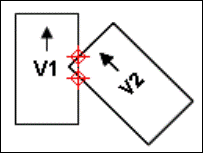
Fig. 3.2.5. ( Zombie Driver - Transport Innovation Software)
Se viene trovata una intersezione o uno dei due elementi in esame è contenuto all’interno dell’altro, viene calcolato l’angolo di collisione tra i vettori o rette (solo nel caso di impatto con veicoli o oggetti elastici). Nel caso di collisione tra veicoli viene prima individuato l’angolo tra i vettori di velocità come differenza tra gli angoli:
![]() = 𝑀𝑎𝑥
= 𝑀𝑎𝑥![]() − Min
− Min![]()
La massa risultate tra i due veicoli è data dall’equazione:
![]() =
=![]()
La differenza vettoriale tra i due vettori di velocità è espressa dalla seguente equazione:
![]() =
=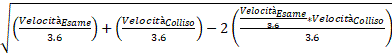
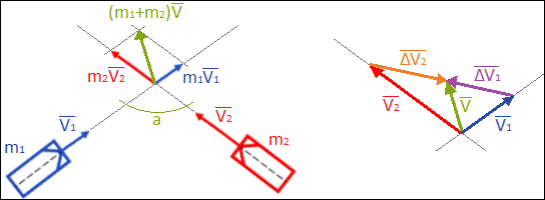
Fig. 3.2.6. ( Zombie Driver - Transport Innovation Software)
L’energia di impatto è pari a
![]() =
=![]() ∆𝑉 2
∆𝑉 2
Per gli oggetti elastici viene individuato l’angolo di collisione mediante il teorema di Carnot o dei Coseni, individuando l’angolo tra le rette.
LineaA
=![]()
LineaB
=![]()
LineaC
=![]()
AngoloFraRetteOstacolo
=![]()
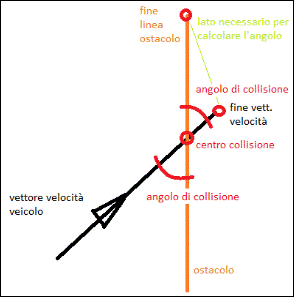
Fig. 3.2.7. ( Zombie Driver - Transport Innovation Software)
L’energia, in joule (kg*m2/s2), che si genera durante l’impatto con un oggetto elastico viene calcolata in funzione del tipo di oggetto impattato:
![]() =
=![]() 𝑆𝑖𝑛(AngoloFraRetteOstacolo)
𝑆𝑖𝑛(AngoloFraRetteOstacolo)
![]() =
=![]()
![]() =
=![]() *
* ![]()
ZombieDriver utilizza inoltre la differenza vettoriale tra i due vettori di velocità (nel caso di collisioni veicolo/veicolo) o con gli ostacoli per ricavare il numero probabile di morti e feriti con o senza cintura.
![]() = (
= (![]() ;
; ![]() = (0.621371 ∗
= (0.621371 ∗![]()
![]() = (0.621371 ∗
= (0.621371 ∗![]() ;
; ![]() = (0.621371 ∗
= (0.621371 ∗![]()
3.3 Tritone
TRITONE (Astarita et al. 2017; Giofrè and Astarita 2014) è un software di micro-simulazione veicolare che permette di rappresentare le situazioni reali di traffico che possono verificarsi su determinate reti stradali. Il software basa il suo funzionamento su modelli in grado di rappresentare singolarmente il movimento di ciascun veicolo, sulla base del comportamento del conducente che segue, tramite le regole dettate dalla teoria dell’inseguitore (Car-Following) (Giofrè et al. 2013, 2015), del cambio di corsia (Lane-Changing), dell’accettazione degli intervalli minimi di accesso agli archi (Gap-Acceptance) e dal sorpasso (Over-taking). In sostanza, i conducenti tendono a viaggiare con la velocità desiderata, ma l'ambiente circostante (i veicoli precedenti, i veicoli adiacenti, la geometria della strada, i segnali stradali ed i semafori, gli ostacoli, ecc.) condiziona il loro comportamento.
Il tempo di simulazione è diviso in piccoli intervalli di tempo chiamati cicli di simulazione oppure intervalli di simulazione o precisione della simulazione (Δt); ad ogni ciclo la posizione e la velocità di ciascun veicolo esaminato nel sistema vengono aggiornate in accordo con le leggi sopra indicate e nel contempo si aggiornano le informazioni sul comportamento macroscopico della rete. L’aggressività e lo stile di guida dei conducenti possono influenzare l’andamento della simulazione, in quanto i guidatori “molto abili” o “aggressivi” hanno tempi di reazione più brevi degli altri; essi possono guidare più vicini agli altri veicoli, possono trovare intervalli di accesso più rapidamente e facilmente, e possono accelerare e frenare repentinamente. Le funzioni di distribuzione, riguardanti le velocità e il distanziamento tra i veicoli, permettono di tener conto del comportamento distinto dei differenti conducenti. La calibrazione dei modello d'accodamento dei veicoli è stata fatta con l’aiuto di numerose sperimentazioni presso il Dipartimento di Ingegneria Civile dell’Università della Calabria. Delle recenti misurazioni garantiscono la modellizzazione corretta del comportamento, che si è evoluto nel tempo, e delle prestazioni tecniche più avanzate dei veicoli. In TRITONE la simulazione del comportamento di un conducente, su una carreggiata a più corsie, non tiene solamente conto dei due veicoli che lo precedono ma anche dei veicoli posti sulle corsie vicine. L’attenzione del conducente è influenzata, inoltre, dai semafori quando il veicolo arriva ad una distanza di circa 20 m. dalla linea d’arresto. Ogni conducente è assegnato, con i parametri che descrivono il suo comportamento, ad un veicolo preciso. Il comportamento del conducente si trova quindi in accordo con le prestazioni tecniche del veicolo. Le caratteristiche che determinano l’unità conducente veicolo possono essere classificate in tre categorie:
1.Specifiche tecniche del veicolo
· lunghezza del veicolo;
· velocità massima;
· accelerazione;
· posizione istantanea del veicolo nella rete;
· velocità e accelerazione istantanea del veicolo.
2. Comportamento dell’unità conducente – veicolo
· limiti psicofisici di percezione del conducente (capacità di stima, percezione della sicurezza, disposizione ad assumere dei rischi);
· memoria del conducente;
· accelerazione in funzione della velocità 2018 in rapporto alla velocità desiderata ed al limite da normativa.
3. Interazione tra
più unità conducente - veicolo
· rapporti fra un determinato veicolo e i veicoli che lo precedono e che lo seguono nella stessa corsia e nelle corsie vicine;
· informazioni riguardanti l’arco di strada utilizzato;
· informazioni concernenti l’impianto semaforico più vicino.
Risulta evidente che l’utilizzo di un micro-simulatore comporta la necessità di descrivere in maniera approfondita e dettagliata tutte le informazioni relative alla domanda ed all’offerta, ma ciò non deve risultare un elemento scoraggiante; infatti si possono evidenziare le seguenti considerazioni. La domanda viene espressa attraverso una o più matrici O/D (ad es. una per il periodo della mattina, una per il periodo centrale della giornata e una terza per il periodo pomeridiano), una curva di distribuzione dei flussi nella giornata (facilmente ricavabile da un campione rappresentativo di rilevazioni continue di traffico), una descrizione della distribuzione tipologica del parco veicoli circolante (ad es. Fonte ACI più indagine a campione sulle percentuali di veicoli pesanti e commerciali), ed una stima della distribuzione tipologica dei conducenti (aggressività di guida, velocità massima, ecc.). Tali informazioni sono ricavabili, attraverso l’applicazione di modelli di stima, da rilevazioni dei flussi di traffico condotte in particolari punti significativi della rete stradale. Giova evidenziare che il modello di micro-simulazione descrive per sua natura in modo assai realistico il comportamento dei veicoli, e fornisce una descrizione decisamente attendibile della realtà, anche a fronte di stime di carattere indicativo di alcuni dei parametri sopra descritti. L’offerta deve essere descritta in termini di geometria plano-altimetrica delle strade e delle intersezioni. Nella realtà, anche tale attività non risulta particolarmente onerosa; infatti, nel software qui proposto, viene assai semplificata dalle procedure di disegno disponibili, in cui la rappresentazione parte da una descrizione schematica costituita da archi e nodi. Fornendo le sole indicazioni relative alla lunghezza della strada, al numero di corsie ed alla pendenza, la strada, nella sua complessità geometrica, viene disegnata automaticamente. All’utente rimane solo il compito di modificare eventuali condizioni particolari. Ulteriori rappresentazioni geometriche (raggi di curvatura, raccordi, ecc.) sono possibili manualmente, al fine di migliorare la qualità della simulazione, di norma già comunque ottima anche in condizioni “standard”. La micro-simulazione fornisce una visione dinamica del fenomeno in quanto, come accennato in precedenza, vengono prese in considerazione le caratteristiche del moto dei singoli veicoli (flusso, densità, velocità, ecc.) non più medie, come accade nei macro-simulatori, bensì reali e variabili istanti per istante durante tutta la simulazione. Attraverso la micro-simulazione è possibile rappresentare più famiglie di spostamenti, ognuna caratterizzata da differenti parametri comportamentali (accelerazione, decelerazione, aggressività, tempo di reazione, ecc.) e da diverse tipologie di veicolo (velocità massima, dimensioni, prestazioni, parametri di emissione, ecc.).
3.3.1 Campi di applicazione di Tritone
TRITONE è un modello di simulazione microscopica della circolazione. Essa viene simulata tenendo conto delle differenti caratteristiche riguardanti la strutturazione delle corsie, la composizione del traffico, la regolazione della precedenza agli incroci e le prestazioni dei veicoli del traffico privato come di quelli del trasporto collettivo. Con TRITONE si possono valutare differenti modi di gestione del traffico attraverso la descrizione qualitativa e quantitativa della circolazione stessa. TRITONE può essere utilizzato per trovare soluzioni ad un gran numero di problemi. Alcuni esempi indicativi possono illustrare il vasto campo di possibilità di impiego di TRITONE:
· Con l’aiuto di TRITONE è possibile effettuare l’analisi della capacità e del funzionamento della circolazione;
· permette di comparare tra di loro diversi scenari progettuali che includono incroci a precedenza regolata da segnaletica, incroci a rotatoria, incroci semaforizzati, incroci a livelli sfalsati, e di valutare la capacità della strada;
· può essere utilizzato per valutare ed ottimizzare operazioni di traffico in reti con la possibilità di riprodurre anche eventi di tipo eccezionale (cantieri, incidenti, emergenze, ecc.) utilizzando una rete viaria il più possibile corrispondente alla realtà (larghezza delle corsie, curvature dei tracciati, altimetrie, strettoie, ecc.) consentendo di ottenere risultati più che mai attendibili.
I molteplici strumenti di rappresentazione offerti dal micro-simulatore consentono di visualizzare e localizzare in modo semplice e veloce i punti critici che si instaurano sulla rete, determinare i tempi di attesa e le code ed individuare le possibili soluzioni ed i percorsi alternativi. A questo proposito è interessante sottolineare che il comportamento dei conducenti può essere modificato agendo su un parametro che specifica il livello di aggressività. I risultati che fornisce il micro-simulatore sono vari e articolati; in particolare, i principali sono:
1. Informazioni sui singoli veicoli
· numero e tipologia di veicoli circolanti sulla rete nel periodo di simulazione;
· velocità media di ciascun veicolo;
· ritardo medio;
· distanza totale percorsa;
· percentuale di veicoli in coda;
· lunghezza della coda;
2. Informazioni sui percorsi
· tempi medi di viaggio.
3. Informazioni sui flussi veicolari e sulle criticità
· istante di memorizzazione dei risultati;
· flussi di manovra alle intersezioni selezionate;
· indici di criticità;
4. Informazioni sugli incidenti
· istante in cui si è verificato;
· tratto di strada interessato;
· durata dell’incidente;
· lunghezza delle code.
5. Informazioni sui parametri ambientali
· emissioni atmosferiche per singolo veicolo;
· emissioni totali per sezione, per arco e per nodo;
· indicatori di criticità ambientale.
6. Indicatori di Safety Performance
· indicatori di criticità DRAC - Deceleration Request Avoid Collision;
· indicatori di criticità TTC - Time to Collision;
· indicatori di criticità PSD – Potential Stopping Distance;
· indicatori di criticità MADR - Maximum Available Deceleration Rate.
7. Modelli di car-following implementati in Tritone
· Gazis e Herman
· Giofrè Avanzato
· Giofrè Lineare
· Giofrè Polinomiale
· Gipps (AIMSUN)
· Van Aerde (Integration)
· Yang (MITSIM)
· FreSim and Intras
· Fritzsche (PARAMICS)
· Wiedemann 1974 (VISSIM)
· Wiedemann 1999 (VISSIM)
· INTAC-12
· NETSIM
· CORSIM
· Krauss (SUMO)
· Intelligent Drive Model 2000
· Chandler
· Leutzbach
· Bando
· Newell
· Nagel
· Personalizzato dall’utente
8. Modelli di cambio di corsia implementati in Tritone
· Giofrè
· MOBIL
9. Modelli di sorpasso implementati in Tritone
· Giofrè 2010
· Giofrè 2016
In particolare, TRITONE dispone di venti modelli di car-following differenti e due di cambio di corsia, utilizzabili per le simulazioni a proprio piacimento, di cui uno può essere addirittura creato dall’utente tramite linguaggio di programmazione e una libreria esterna già predisposta e presente nella cartella di TRITONE.
CAPITOLO 4 - Scenario di studio
4.1 Inquadramento territoriale
La strada statale 106 Jonica (SS 106) si estende per 491 km dal comune di Reggio Calabria a quello di Taranto, attraversando tre regioni Calabria, Basilicata e Puglia. Essa costituisce una direttrice di traffico di rilevanza nazionale ed è ricompresa nella Strada europea E90.
Fig.4.1. Tracciato Strada Statale 106 jonica (fonte Web)
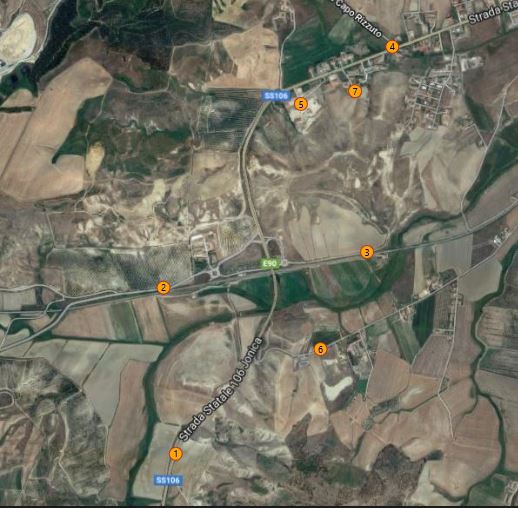
Nella provincia di Crotone, quella presa in esame dal lavoro di tesi la SS si snoda attraverso i territori di Cutro (frazione di Steccato e Marina di Cutro) e di Isola di Capo Rizzuto (frazioni di Le Castella e Sant'Anna), lambendo l'aeroporto di Crotone. La strada statale 106 entra poi nella periferia di Crotone, nel quartiere meridionale di Poggio Pudano e nelle aree commerciale e industriale, passando esternamente al centro urbano. Oltrepassata la città di Crotone vi è l'intersezione con la strada statale 107 Silana Crotonese per la Sila per Cosenza. Numerose indagini sui dati raccolti dalla Polizia Stradale hanno classificato la statale jonica 106 come l’arteria che fa registrare il numero più alto di incidenti con danni alle persone, ben 345 nel 2014, che hanno provocato 14 morti e 672 feriti. Entrando nel dettaglio dello studio eseguito sulla cosiddetta “strada della morte”, emerge che tra le province calabresi che attraversa, quella di Crotone risulta quella con il più alto indice di mortalità (8,5 decessi ogni 100 incidenti). L’area presa in considerazione dal lavoro di tesi fa riferimento alla porzione compresa tra località Sant’Anna (Kr) e Steccato di Cutro (Kr).
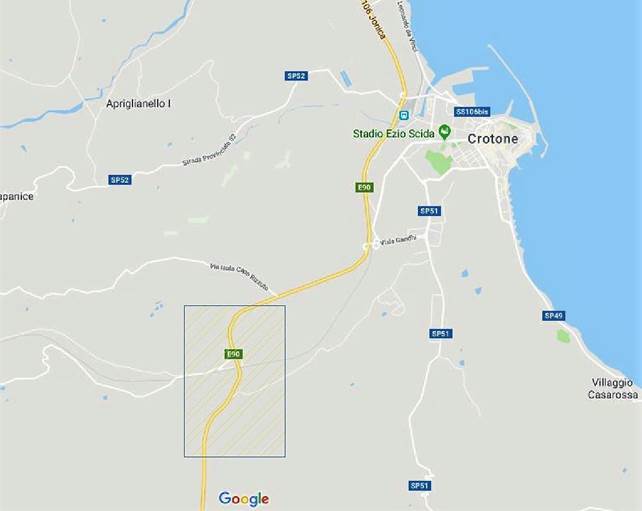
Fig.4.1.1 Inquadramento area di studio (fonte Google Maps)
Il tracciato in esame è composto da un’unica carreggiata a doppio senso di circolazione con un andamento altimetrico pressoché regolare che si snoda alternando lunghi rettilinei e curve ad ampio raggio. L’ andamento scorrevole della statale ed in particolare i lunghi rettilinei inducono gli utenti a mantenere velocità elevate anche in prossimità delle corsie di accelerazione e decelerazione che garantiscono l’accesso e l’egresso degli utenti direzione Nord e Sud. La presenza di accessi lato Est ed Ovest fa sì che l’infrastruttura sia soggetta ad una mescolanza di flussi eterogenei per tipologia e caratteristiche del moto. Le principali problematiche tecniche che affliggono l’infrastruttura sono da imputare alla scarsa manutenzione dello strato d’usura e dei sistemi di ritenuta, inoltre vi è lungo tutto il tratto in esame una distanza minima tra linea di demarcazione e manufatti di controripa.
4.2 Modellizzazione rete con Tritone
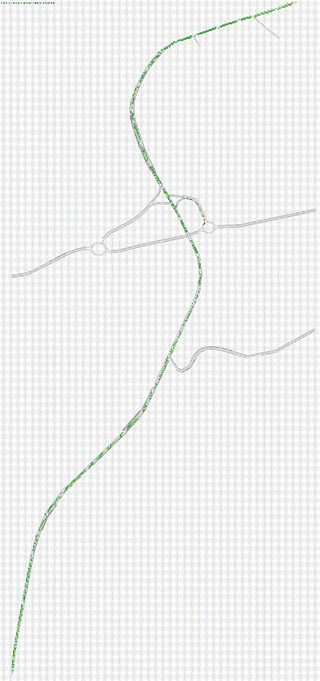
La micro-simulazione ci consente di riprodurre la realtà in ambiente virtuale e di effettuare considerazioni su possibili scenari o eventi, senza che questi si verifichino realmente. I microsimulatori basano il loro funzionamento su modelli in grado di rappresentare singolarmente il movimento di ciascun veicolo sulla base del comportamento del conducente, che segue le regole dettate dalla teoria dell’inseguitore (Car-Following), da quella del cambio corsia (Lane-Changing), da quelle dell’intervallo minimo di accesso (Gap-Acceptance), dal sorpasso (Over-taking) e da tanti altri. In sostanza, i conducenti tendono a viaggiare alla velocità desiderata, ma l'ambiente circostante (i veicoli precedenti, i veicoli adiacenti, la geometria della strada, i segnali stradali ed i semafori, gli ostacoli, ecc.) condiziona il loro comportamento. Il tempo di simulazione è diviso in piccoli intervalli di tempo chiamati cicli di simulazione oppure intervalli di simulazione (Δt); ad ogni ciclo la posizione e la velocità di ciascun veicolo esaminato nel sistema vengono aggiornate in accordo con i modelli e nel contempo si aggiornano le informazioni sul comportamento macroscopico della rete. L’aggressività e lo stile di guida dei conducenti possono influenzare l’andamento della simulazione, in quanto i guidatori “molto abili” o “aggressivi” hanno tempi di reazione più brevi degli altri; essi possono guidare vicino ai veicoli precedenti, possono trovare intervalli di accesso più rapidamente e possono accelerare e frenare repentinamente. La porzione di infrastruttura che si estende per 11698.32 m, è collocata in località di Sant’Anna, Crotone. Nell’area di studio sono state individuate, in linea di massima, la posizione delle abitazioni, dei negozi, degli uffici, delle industrie, ecc., e si è cerca di tracciare delle linee di separazione tra queste, in maniera tale da ottenere delle aree omogenee. La rete è stata modellizzata mediante la teoria dei grafi, ovvero mediante nodi e archi. Gli archi rappresentano le strade, per senso di marcia, in maniera di semplice retta orientata secondo la segnaletica stradale. I nodi possono invece essere di due tipi fisici, quando rappresentano un’intersezione o un altro elemento realmente presente sulla rete stradale, e fittizi chiamati centroidi, quando rappresentano un punto di origine o di destinazione dei flussi veicolari. Nella pratica i centroidi vengono fatti coincidere con il centro della massa di una zona, e vengono poi collegati alla rete con degli archi fittizi. I dati di ogni arco sono generalmente la lunghezza, la capacità, la velocità limite imposta dal codice della strada, il numero di corsie, il senso di marcia, la presenza di segnaletica, le manovre permesse, e la pendenza. Per i nodi invece l’unica cosa che interessa, in quanto rappresentazione delle intersezioni, è se c’è o meno la presenza di un impianto semaforico per la lettura dei tempi delle fasi di verde, giallo e rosso.
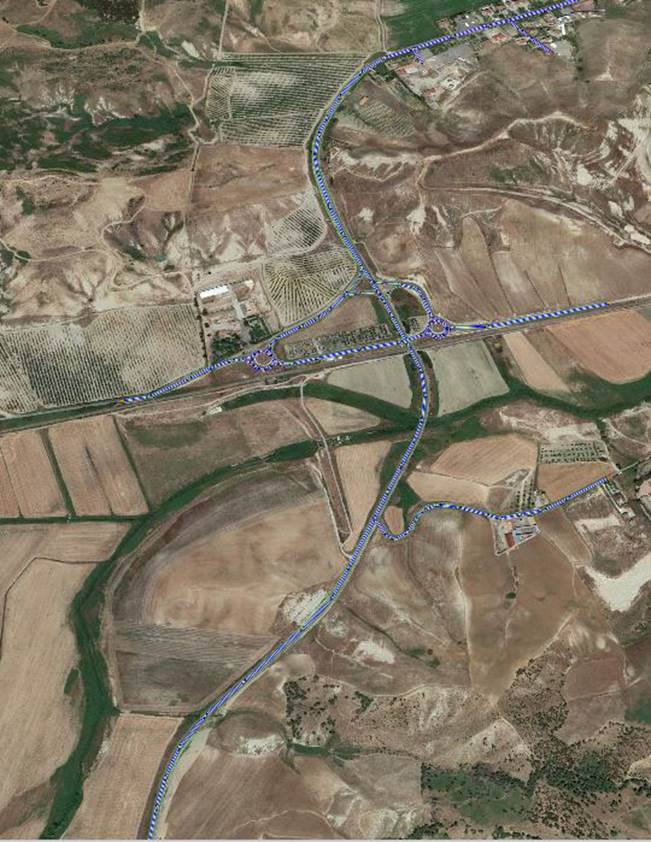
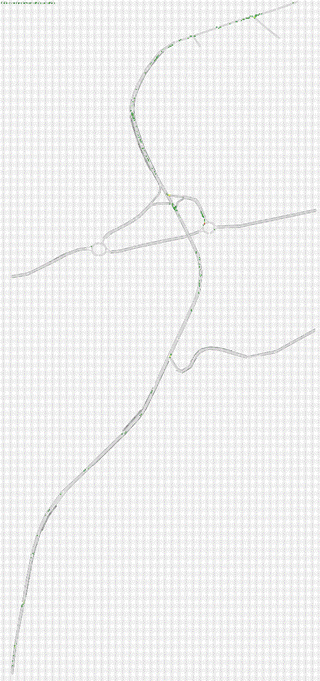
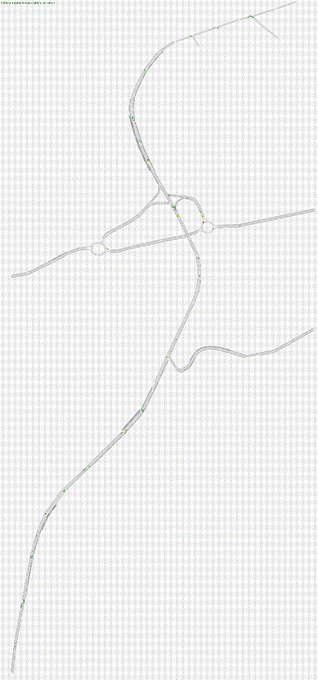
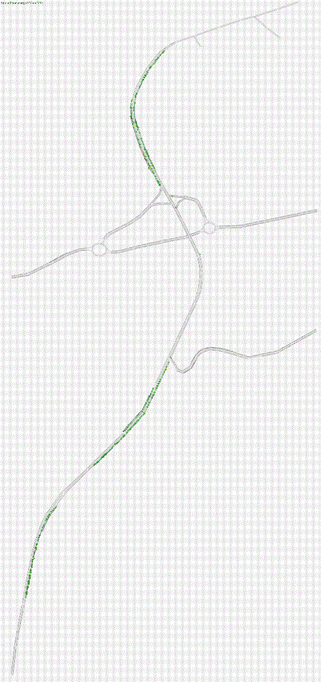
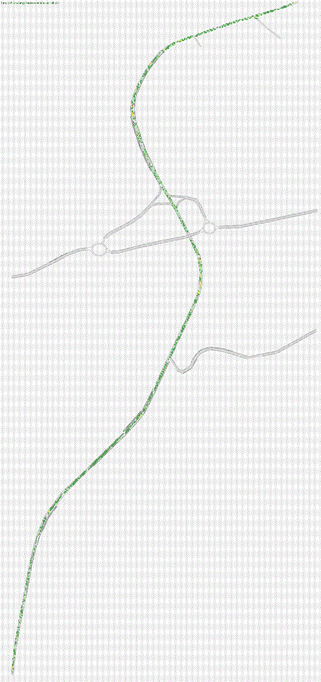
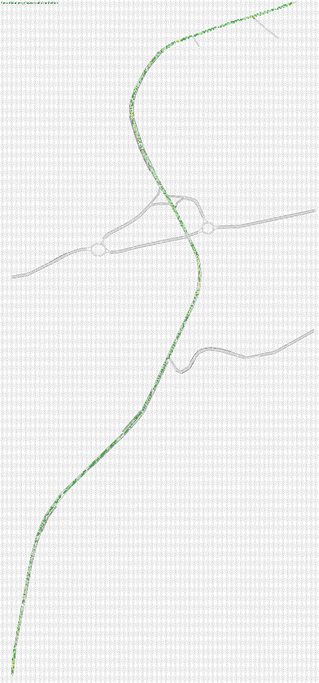
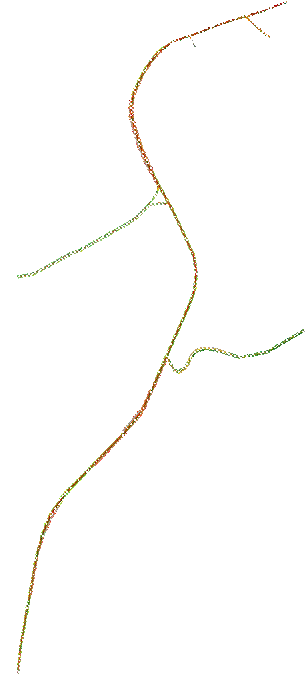
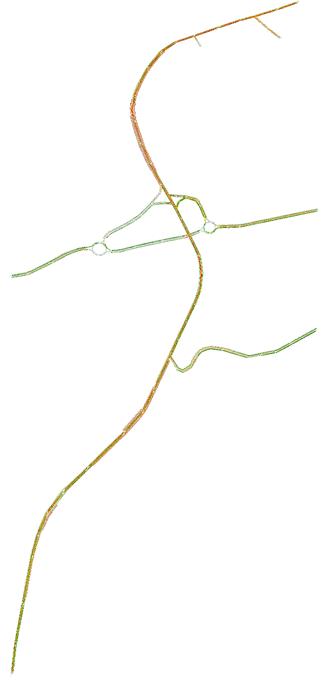
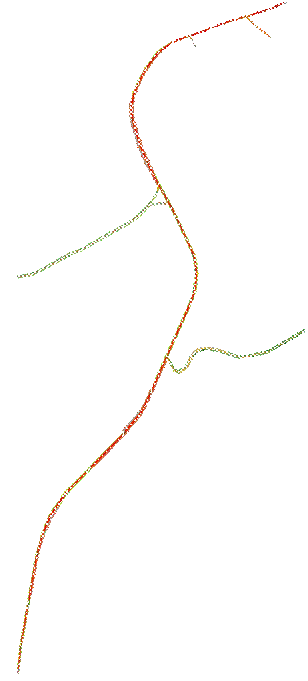
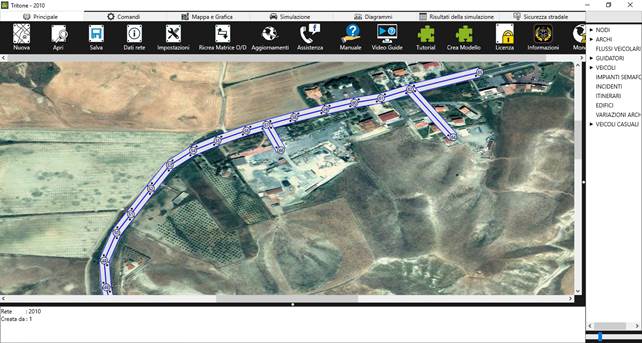
Fig.4.2. Rete Stato 2018 modellizzata attraverso Tritone
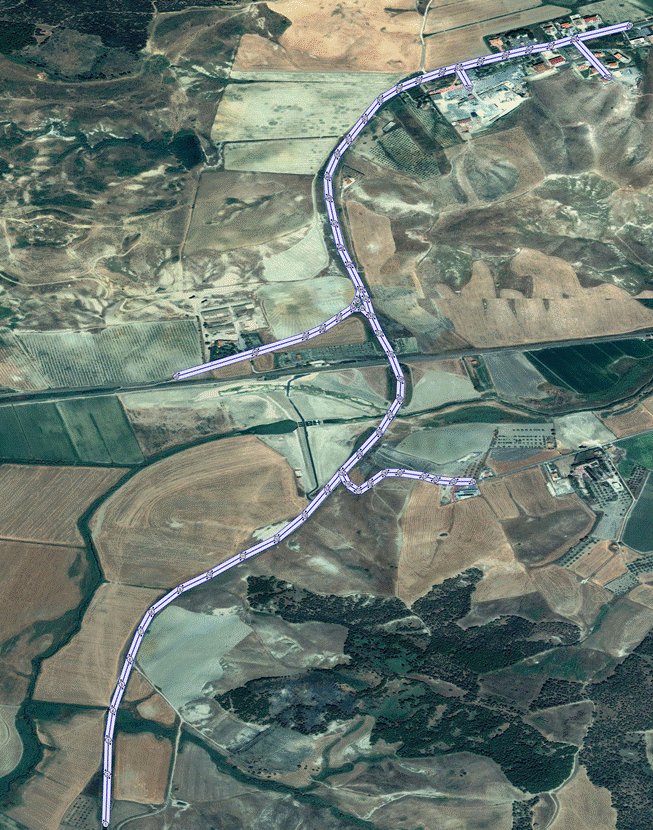
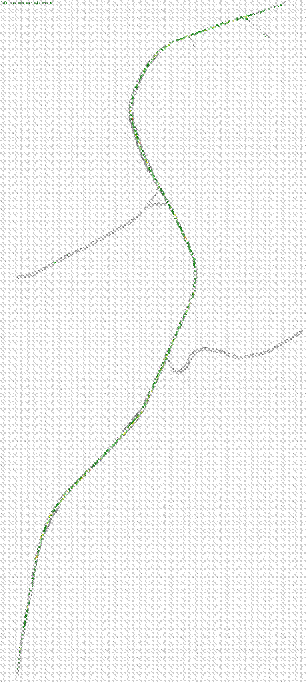
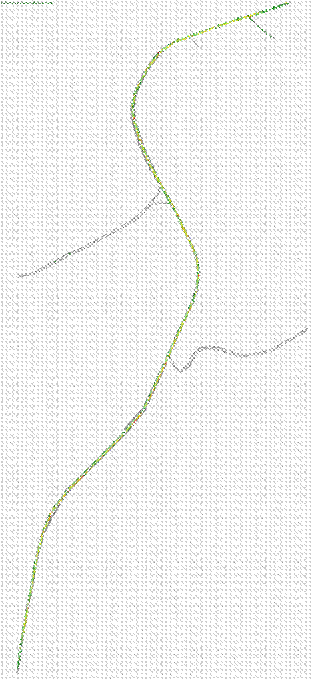
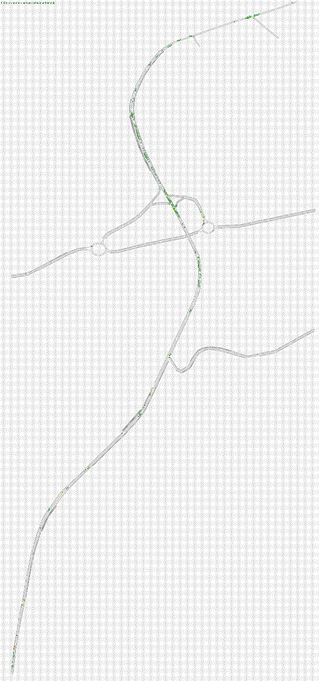
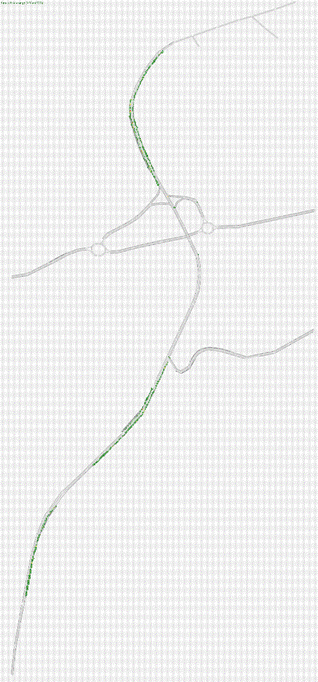
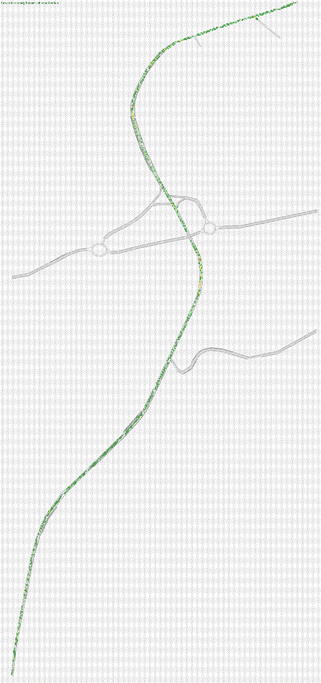
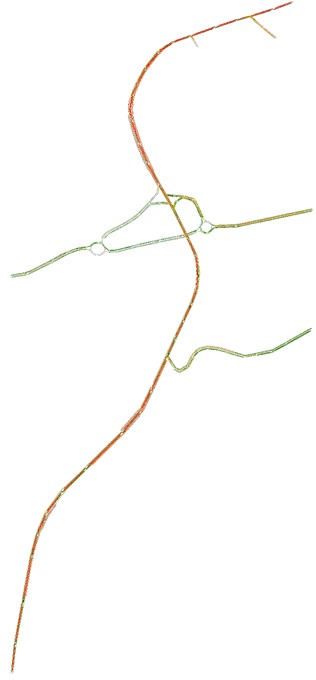
Fig.4.2.1 Rete Stato 2010 modellizzata attraverso Tritone
4.3 Stima della domanda
Per la stima della domanda si è provveduto in prima istanza ad una fase elaborazione del rilievo datato 2010 per l’individuazione delle intersezioni e per il collocamento dei nodi centroidi. In un secondo momento è stato necessario inserire nel software i flussi in entrata ed in uscita da ogni centroide considerando due categorie di veicoli: auto e veicoli pesanti. In seguito, sono riportate le Matrici O/D per lo stato 2010 e 2018
|
AUTOMOBILI 2018 |
|||||||
|
O/D |
22 |
58 |
60 |
61 |
105 |
106 |
1 |
|
1 |
60 |
240 |
480 |
120 |
240 |
60 |
0 |
|
22 |
0 |
0 |
20 |
0 |
0 |
0 |
20 |
|
58 |
0 |
0 |
50 |
0 |
0 |
0 |
50 |
|
60 |
60 |
240 |
0 |
120 |
240 |
60 |
480 |
|
61 |
0 |
0 |
20 |
0 |
0 |
0 |
20 |
|
105 |
0 |
0 |
50 |
0 |
0 |
0 |
50 |
|
106 |
0 |
0 |
20 |
0 |
0 |
0 |
20 |
|
MEZZI PESANTI 2018 |
|||||||
|
O/D |
22 |
58 |
60 |
61 |
105 |
106 |
1 |
|
1 |
6 |
24 |
48 |
12 |
24 |
6 |
0 |
|
22 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
|
58 |
0 |
0 |
5 |
0 |
0 |
0 |
5 |
|
60 |
6 |
24 |
0 |
12 |
24 |
6 |
48 |
|
61 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
|
105 |
0 |
0 |
5 |
0 |
0 |
0 |
5 |
|
106 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
|
AUTOMOBILI 2010 |
||||||
|
O/D |
67 |
38 |
40 |
52 |
68 |
1 |
|
1 |
60 |
240 |
480 |
120 |
60 |
0 |
|
67 |
0 |
0 |
20 |
0 |
0 |
20 |
|
38 |
0 |
0 |
50 |
0 |
0 |
50 |
|
40 |
60 |
240 |
0 |
120 |
60 |
480 |
|
52 |
0 |
0 |
20 |
0 |
0 |
20 |
|
68 |
0 |
0 |
20 |
0 |
0 |
20 |
|
MEZZI PESANTI 2010
|
||||||
|
O/D |
67 |
38 |
40 |
52 |
68 |
1 |
|
1 |
6 |
24 |
48 |
12 |
6 |
0 |
|
67 |
0 |
0 |
2 |
0 |
0 |
2 |
|
38 |
0 |
0 |
5 |
0 |
0 |
5 |
|
40 |
6 |
24 |
0 |
12 |
6 |
48 |
|
52 |
0 |
0 |
2 |
0 |
0 |
2 |
|
68 |
0 |
0 |
2 |
0 |
0 |
2 |
La rete allo stato 2018 presenta delle variazioni, in particolare dovute all’introduzione di un nuovo svincolo di acceso ed egresso lato EST:
· 12576,63 m di strada con limite di velocità pari a 90 km/h su strada principale e 50 km/h su strade secondarie
· illuminazione presente a esclusivamente nelle vicinanze delle abitazioni nella parte superiore della rete
4.4 Modelli di Simulazione
La micro-simulazione ci consente di riprodurre in maniera fedele quelli che sono le iterazioni che avvengo tra i veicoli e tra i veicoli e l’infrastruttura. In generale i modelli si dividono in:
· modelli macroscopici: utilizzano relazioni d’insieme e individuano proprietà e variabili di stato globali; il flusso veicolare viene analizzato da un punto di vista globale, i parametri fondamentali che entrano in gioco sono i flussi, la velocità e la densità relativamente ad una intera corrente veicolare.
· modelli mesoscopici: la corrente veicolare viene trattata ad un livello di aggregazione intermedio; in pratica i veicoli vengono considerati in gruppi omogenei. Tali modelli forniscono, in termini probabilistici, la variabilità dei parametri del deflusso.
· modelli microscopici: descrivono il comportamento del traffico con un alto livello di dettaglio, fino a considerare il singolo veicolo; descrivono il comportamento dei singoli veicoli come risultato di scelte individuali legate alle interazioni con gli altri veicoli e con l’ambiente stradale. Ai parametri di deflusso si aggiungono i fattori che influenzano la scelta di percorso, il cambio di velocità, cambio di corsia, stile di guida, tempo di percezione e reazione, velocità desiderata, ecc.
· modelli ibridi: trattano alcune parti con un modello e altre con un altro, ad esempio il flusso principale di un’arteria importante con il modello microscopico e le rampe di accesso all’arteria stessa con il modello macroscopico.
Nel caso in esame sono stati utilizzati modelli microscopici, i quali simulando il comportamento del veicolo e fornendo gli elementi per una dettagliata analisi quantitativa risultano i più adatti alla simulazione realistica della realtà in maniera dinamica. In dettaglio sono stati utilizzati all’interno del software: Modello di Car Following, Modello Lane Changing, Modello Overtaking, Modello Gap Acceptance, Modello di Generazione del Taffico, Modello di Scelta del Percorso.
4.4.1 Modello di Car-Following
Ciascun conducente tende a raggiungere una velocità prescelta sulla base del suo stile di guida, delle prestazioni del veicolo che guida, e delle caratteristiche geometriche della strada che sta percorrendo. Se durante la marcia raggiunge un veicolo che lo precede, dovrà rallentare e adeguare la sua velocità o, se ciò è possibile, cambiare corsia. Il problema principale della simulazione microscopica è la scelta del modello matematico di car-following da utilizzare, perché questo può influire drasticamente sui risultati.
Modello di Gazis-Herman (General Motors): I modelli di car-following sviluppati dai ricercatori associati al gruppo General Motors (1950) furono molto ampi e sono di particolare importanza a causa dei numerosi esperimenti condotti sul campo e per la scoperta di un ponte tra teoria microscopica e macroscopica del flusso di traffico. Il gruppo di ricerca sviluppò cinque categorie di modelli di car-following. L’espressione generale di un modello di car-following è dato da:
![]()
La risposta è nota come accelerazione del veicolo, a seguito di uno stimolo causato dalla differenza di velocità del veicolo che precede e dei veicoli che seguono. La sensibilità è un parametro comportamentale che dipendere dalle differenze di velocità e di frequenza dei plotoni. Il modello generale del GM è stata sviluppato dal gruppo di ricerca General Motors (Gazis, Herman, and Potts 1959; Gazis, Herman, and Rothery 1961; Herman et al. 1959; Herman and Rothery 1969). Il fattore di sensibilità dipende dagli spazi e dalle velocità dei veicoli che seguono. L'espressione matematica è data dalla seguente equazione:
![]()
dove:
· d: distanza fra i veicoli
· an+1(t + Δt): accelerazione o decelerazione del veicolo in esame al tempo t + Δt
· αl,m: parametro di sensibilità
· Δt: tempo di reazione del conducente del veicolo in esame
· Vn(t): velocità del veicolo che precede al tempo t
· Vn+1(t): velocità del veicolo in esame al tempo t
· l e m: esponenti di distanza e velocità preselezionati.
Imponendo m = 0 e l = 0 si ottiene la prima e la seconda formulazione del modello (Chandler, Herman, and Montrol 1958)
![]()
![]()
dove:
· α: parametro di sensibilità costante
· α1: il valore maggiore di α quando i due veicoli sono vicini tra loro
· α2: in valore minore di α quando i due veicoli sono distanti
I modelli sviluppati da Chandler (Chandler et al. 1958) e Gazis (Gazis et al. 1959) possono essere visti come casi particolari del modello generalizzato. Imponendo m = 0 e l = 1, otteniamo il terzo modello GM da cui può essere derivato il modello macroscopico di Greenberg (Greenberg 1959).
![]()
dove:
α0 = parametro di sensibilità in metri/sec
Il quarto modello è stato un ulteriore sviluppo verso il miglioramento del termine di sensibilità introducendo la velocità del veicolo a seguito dell’evento. Il concetto è che la velocità del flusso aumenta il traffico, il conducente del veicolo è più sensibile alla velocità relativa tra il veicolo che precede e il suo. Inoltre, impostando m = 1 e l = 1, si ottiene il quarto modello GM che può essere espresso come:
![]()
In questa formulazione il termine di sensibilità ha tre componenti: una costante α, la velocità del veicolo a seguito dell’evento, e la distanza fra i due veicoli. Sono stati fatti molti tentativi per determinare i valori esatti di l e m. Treiterer e Myers (1974) propongono l = 1.6, m = 0.2 e l = 2.5, m = 0.7 per accelerazione e decelerazione, rispettivamente, con un approccio microscopico. Hoefs (1972), impiegando anche un approccio microscopico, arriva a un insieme diverso di l e m per i valori di accelerazione e decelerazione, con e senza rottura, rispettivamente. Più di recente, Ozaki (1993) ha tentato di stime α, l, ed m ma i suoi valori sono stati contraddittori a quelli osservati dai ricercatori precedenti. Ozaki, tuttavia, ha osservato che gli spazi e l'accelerazione dei veicoli che precedono hanno un effetto sul tempo di reazione.
Modello di Gipps (AIMSUN - Safe distance model): Il comportamento di AIMSUN è modellato utilizzando il modello di car-following di Gipps del 1981 (Gipps 1981) secondo cui la velocità del veicolo che segue è controllata da tre condizioni. La prima condizione assicura che il veicolo non superi la velocità desiderata o la velocità a flusso libero, la seconda condizione assicura che il veicolo acceleri fino alla sua velocità desiderata, con un incremento di accelerazione che aumenta quando si è ancora alla velocità iniziale e poi diminuisce fino a zero quando si avvicina alla velocità desiderata. I coefficienti dell'equazione sono stati ottenuti da una curva di interpolazione da dati raccolti su una strada a traffico moderato. In condizione di flusso libero la velocità risulta:
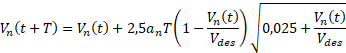
dove:
· Vn(t): velocità della vettura n al tempo t in m/sec
· an: accelerazione massima in m/s2
· T: tempo di reazione del conducente in secondi
· Vdes: velocità desiderata o velocità a flusso libero in m/sec
In una situazione di traffico limitato, quando i veicoli viaggiano vicini tra loro, la terza condizione diventa dominante e controlla il comportamento del veicolo e la velocità del veicolo è influenzata dal tempo di reazione del conducente. Gipps ha sottolineato che deve essere aggiunto un margine di sicurezza al tempo di reazione del conducente, pari a T/2, e che ciò avrebbe assicurato la capacità al veicolo di fermarsi. Da ciò è quindi possibile ottenere l’equazione nel campo di una condizione di car-following come:
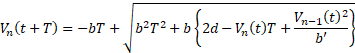
dove:
· b: decelerazione massima del veicolo in esame in m/s2
· b’: è funzione delle decelerazioni tra i veicoli in m/s2
![]()
· d: distanza tra i veicoli
Questi parametri influenzano lo spazio tra i veicoli e quindi incide sulla capacità della corsia. La velocità può dunque essere calcolato come:
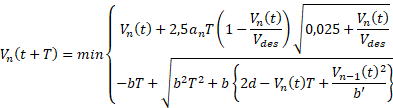
Secondo questa formulazione una volta che la strada è libera o lo spazio tra i veicoli è grande abbastanza da permettere loro di viaggiare alla velocità desiderata, si utilizza la prima equazione, altrimenti la seconda. Ogni veicolo stabilisce la sua velocità in modo da evitare una collisione basandosi sul presupposto che la decelerazione del veicolo “a” che precede non supererà “b”
Modello IDM 2000 (Intelligent Drive Model): Questo è modello di car-following continuo valido per autostrade e traffico urbano. E’ stato sviluppato da Treiber nel 2000 (Treiber, Hennecke, and Helbing 2000) per migliorare i risultati ottenuti con gli altri modelli intelligenti, come il Gipps (Gipps 1981), che perdono le proprietà realistiche nel limite deterministico. In condizioni di flusso libero l’equazione dell’accelerazione è pari a:
![]()
Mentre in condizione di car-following si ha:
![]()
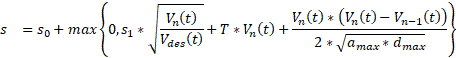
|
parametri |
automobili |
veicoli pesanti |
unità misura |
|
|
δ |
4 |
4 |
4 |
|
|
T |
1,6 |
1,5 |
1,7 |
sec |
|
amax |
0,73 |
1 |
0,3 |
m/s2 |
|
dmax |
1,67 |
3 |
2 |
m/s2 |
|
Vdes |
120 |
108 |
80 |
Km/h |
|
s0 |
2 |
2 |
2 |
m |
|
s1 |
0 |
0 |
0 |
m |
|
Lung.veic. |
5 |
5 |
5 |
m |
Dove δ è un parametro di calibrazione, T il tempo di sicurezza, s* rappresenta lo spazio minimo desiderato, s0 la distanza minima di sicurezza e s1 è necessario solo per alcune funzioni che richiedono un punto di svolta nel bilancio del rapporto portata/densità. I coefficienti dedotti da calibrazioni sono:
Il modello prevede quattro casi:
Traffico in equilibrio. In questo caso, i conducenti tendono a mantenere la velocità a seconda della distanza vn=0, ∆v=0, o è se, data da:
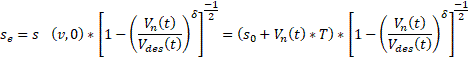
In particolare, in casi di congestione omogena:
![]()
Accelerazione alla velocità desiderata. Se la densità di traffico è bassa, l'accelerazione è data dall’accelerazione libera:
![]()
Il comportamento più realistico per δ (spiegare come l’accelerazione diminuisce quando ci si avvicina alla velocità desiderata) è compreso tra 1 (nessuna accelerazione esponenziale) e ∞(accelerazione costante).
Rallentamento come reazione all’avvicinamento. Quando ci si avvicina a veicoli con velocità inferiori (∆v > 0) l'equazione di equilibrio è della distanza desiderata si sostituisce s0+v*T per v*Δv. Nell'equazione di accelerazione viene sostituito a (s*/d)2 per (v*Δv)2/(4dmins2) che è l’espressione che anticipa il comportamento di frenata "intelligente". Se ci si avvicinano all’ostacolo, Δv = v e la decelerazione minima per evitare l’impatto è v2/(2s).
Frenata come reazione a piccoli spazi. Ciò accade quando lo spazio tra i veicoli è molto piccolo dello spazio desiderato (ma le velocità non sono molto differenti), allora l'equazione della velocità diventa:
![]()
I punti di forza sono:
· Il modello è molto semplice e funziona anche per situazioni di congestione.
· Viene applicato in più di un centinaio di casi e non riesce sono a spiegare il comportamento come le strozzature dovute al sorpasso tra camion.
· Mentre le debolezze sono:
· Le semplificazioni sono tali da avere solo un parametro di calibrazione.
· Non prendere in considerazione sorpasso.
· Non tiene conto che il comportamento umano è variabile.
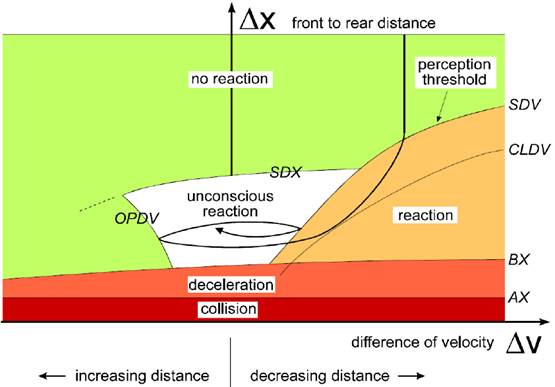
Modello di Wiedemann (1999) (Vissim): Il modello di Wiedemann del 1999 (Fellendorf and Vortisch, 2010) è stato sviluppato come semplificazione del modello del 1974 (Wiedemann, 1991, 1974). Anch’esso funziona mediante degli stati delimitati da tre soglie di avvicinamento tra i veicoli. Le soglie definiscono i regimi di guida libera, avvicinamento, molto vicino, following, following in accelerazione, following in decelerazione e un regime di emergenza. Il modello è funzione dei parametri riportati nella tabella successiva.
|
Ambito |
Parametro |
Significato |
Valore |
|
Spazio |
CC0 |
Distanza di arresto: Distanza desiderata a Velocità = 0 km/h, tra il veicolo in esame e quello che lo precede |
1,5 m |
|
CC1 |
Headway Temporale: Distanza temporale desiderata, in secondi, tra il veicolo in esame e quello che lo precede |
0,9 s |
|
|
CC2 |
Variazione del veicolo in esame: Distanza aggiuntiva alla distanza di sicurezza che un veicolo richiede |
4,0 m |
|
|
CC3 |
Soglia per l’entrata nello stato di Following: Tempo in secondi prima che un veicolo inizia a rallentare per raggiungere la distanza di sicurezza (negativo) |
-8,0 |
|
|
Velocità |
CC4 |
Soglia negativa per lo stato di Following: Specifica variazione di velocità tra il veicolo in esame e quello che lo precede |
-0,35 |
|
CC5 |
Soglia positiva per lo stato di Following: Specifica variazione di velocità tra il veicolo in esame e quello che lo precede |
+0,35 |
|
|
CC6 |
Velocità dipende dall’oscillazione: Influenza della distanza sulle oscillazioni di velocità |
11,4 |
|
|
Accelerazione |
CC7 |
Oscillazione dell’accelerazione: Accelerazione durante il processo di oscillazione |
0,25 m/s2 |
|
CC8 |
Accelerazione da fermo: Accelerazione desiderata partendo da fermo |
3,5 m/s2 |
|
|
CC9 |
Accelerazione a 50 mph: Accelerazione desiderata a 50 mph (80,47 km/h) |
1,5 m/s2 |
I parametri da CC0 a CC6 sono utilizzati per determinare le soglie degli stati del modello.
Differenza di velocità tra due veicoli:
![]()
Distanza tra due veicoli calcolata dal paraurti anteriore al paraurti anteriore:
![]()
Dove Ln-1 è la lunghezza del veicolo che precede.
Distanza minima tra veicoli fermi:
![]()
Distanza minima desiderata:
![]()
![]()
![]()
Distanza massima desiderata:
![]()
Soglia alla quale il veicolo in esame riconosce che si sta avvicinando ad un veicolo più lento:
![]()
Soglia per la differenza di velocità in un processo di avvicinamento di due veicoli durante lo stato di following:
![]()
Soglia per la differenza di velocità in un processo di allontanamento di due veicoli durante lo stato di following:
![]()
Dove δ è una variabile dicotomica e vale:
![]()
Queste soglie danno luogo ai seguenti regimi:
Guida libera: Il veicolo si trova sopra tutte le soglie del diagramma e il viaggio non è influenzato dal traffico circostante ([Dv < SDV e Dx ≥ SDX] o [Dv < OPDV e Dx ≥ ABX]). Il veicolo utilizza la sua massima accelerazione per raggiungere la velocità desiderata.
![]()
![]()
Dove vmax è la velocità massima del veicolo, BMAXmult e FAKTORVmult sono due parametri di calibrazione.
Avvicinamento: si verifica quando un veicolo, che si trova nel regime di guida libera, passa la soglia di percezione (CLDV > Dv ≥ SDV e Dx ≥ ABX). Il veicolo decelera secondo l'equazione:
![]()
Molto vicino: si verifica solo quando un veicolo che si trova nel regime di avvicinamento, passa soglia di velocità in un processo di avvicinamento di due veicoli (Dv ≥ CLDV e Dx ≥ ABX). In VISSIM questo regime viene ignorato, quindi la decelerazione è ancora calcolata l'equazione del regime di avvicinamento.
Following: questo regime (OPDV ≤ Dv < SDV o ABX ≤ Dx < SDX) prevede due sotto regimi, uno di decelerazione e uno di accelerazione. L'accelerazione è negativa e calcolata come:
![]()
Dove BNULLmult è un parametro di calibrazione, RND4n rappresenta l’abilità del guidatore di controllare l’acceleratore e deriva da una distribuzione normale, NRND è un numero casuale distribuito anch’esso secondo una distribuzione normale.
Following - Decelerazione: si verifica quando un veicolo, che si trova nel regime di avvicinamento o in un regime molto vicino, passa la soglia di percezione SDV o un veicolo, che si trova nel regime di accelerazione, passa la seconda soglia di percezione SDX. L'accelerazione è negativa e calcolata come:
![]()
Following - Accelerazione: si verifica quando un veicolo, che si trova nel regime di decelerazione, passa la soglia OPDV della differenza di velocità in un processo di allontanamento, o un veicolo, che si trova nel regime di emergenza, passa la soglia ABX della distanza minima desiderata. L'accelerazione è positiva e calcolata come:
![]()
Se un veicolo, che si trova in questo regime, supera la soglia della distanza massima desiderata, entrerà nel regime di guida libera.
Regime di emergenza: si verifica quando la distanza fra i veicoli è inferiore a ABX (Dx < ABX), e il conducente adotta una decelerazione per evitare la collisione con il veicolo che precede:
![]()
Dove la decelerazione massima del veicolo è calcolata come:
![]()
Dove BMINadd e BMINmult sono parametri di calibrazione, mentre RND3n è un parametro del guidatore distribuito secondo una distribuzione normale.
4.4.2 Modello di Lane Changing
Ciascun conducente stabilisce, istante per istante, l’opportunità o meno della manovra di cambio corsia sulla base della necessità, della desiderabilità e dell’attuabilità della manovra. L’altra modellizzazione importante da fare riguarda il comportamento di cambio corsia che è anche una componente vitale dei modelli microscopici di simulazione del traffico. I cambi possono verificarsi ogni volta che c'è un bisogno di movimento maggiore, aumento di velocità sulle autostrade o per evitare i veicoli in uscita. Le possibilità di cambio di corsia sono disponibili in condizioni di traffico leggero, dove non si verifica la congestione. Un cambio di corsia è considerato fattibile se c'è un gap di dimensioni sufficienti nella corsia di destinazione in modo che il veicolo possa spostarvisi in modo sicuro, senza forzare gli altri veicoli presenti in essa o farli rallentare in modo significativo. Per questo caso si è scelto di utilizzare il modello matematico di Giofrè. Esso è un modello di cambio corsia, sviluppato presso il Dipartimento di Ingegneria Civile dell’Università della Calabria, nel quale gli aspetti predominanti sono le distanze tra i veicoli delle corsie adiacenti a quella in esame. Affinché avvenga il cambio di corsia si deve avere abbastanza spazio sia tra il veicolo in esame e il suo futuro leader che fra lo stesso e quello che si trova dietro nella futura. Inoltre, è presente un controllo che fa sì che l’auto che viaggia su una corsia che si perde, deve passare obbligatoriamente sulla corsia inferiore o fermarsi in attesa di avere lo spazio necessario ad effettuare la manovra.
4.4.3 Modello di Overtaking
Ciascun conducente stabilisce, istante per istante, l’opportunità o meno della manovra di sorpasso sulla base della necessità, della desiderabilità e dell’attuabilità della manovra.Per questo caso si è scelto di utilizzare il modello matematico di Giofrè 2016.Se la strada possiede una corsia per senso di marcia ed è di tipo bidirezionale, allora nell’ipotesi che vi sia uno o più veicoli che precedono a velocità basse, alcuni utenti sentiranno la necessità di eseguire una manovra di sorpasso. Con questo modello ciò può avvenire solo nelle ipotesi in cui la strada sia di tipo bidirezionale con una sola corsia per senso di marcia, che la distanza di inserimento sia abbastanza ampia, che l’utente sia desideroso di andare a una %V0 superiore all’unità, che la distanza col veicolo che procede nel senso opposto sia superiore a quella necessaria per eseguire la manovra di sorpasso e che la distanza col veicolo che precede nello stesso senso di marcia, sia inferiore a quella di sicurezza, altrimenti l’eseguire la manovra non avrebbe senso.
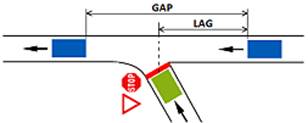
4.4.4 Modello di Gap-Acceptance
Ciascun conducente stabilisce quando eseguire una manovra (cambiare corsia, attraversare un’intersezione, inserirsi in un flusso di traffico, entrare in una rotatoria, ecc.) valutando se esiste l’intervallo temporale minimo necessario per la manovra, sulla base delle velocità relative degli altri veicoli. Questo modello entra principalmente in gioco quando un veicolo giunge ad una intersezione. Affinché il veicolo in esame possa accedere all’arco successivo e completare la manovra di svolta è necessario che ci siano dei GAP e LAG adeguati alla sua velocità.
4.4.5 Modello di Generazione del Traffico
Altro fattore rilevante durante una simulazione è il modello con cui si generano i veicoli sulla rete, in quanto questi possono essere immessi principalmente in tre modi differenti, costante, uniforme, esponenziale, ed influenzano in maniera significativa il risultato della simulazione. L'intervallo di tempo τ tra due arrivi consecutivi di veicoli è governato da una distribuzione casuale del modello di assegnazione. Il tempo medio ∆t tra due arrivi è paria a:
Δt = (Tf – Ti) / Fveicoli = 1 / λ
Per questo caso si è scelto di utilizzare la distribuzione constant
Con questo tipo di distribuzione gli intervalli di tempo tra due arrivi consecutivi sono sempre costanti e l'algoritmo per il calcolo del tempo di progressione è il seguente:
τ = Δt = 1 / λ
4.4.6 Modello di Scelta del Percorso
Tassello fondamentale della modellizzazione di una rete stradale è il calcolo dei percorsi minimi che di solito avviene mediante l’algoritmo iterativo di Dijkstra che calcola, per ogni centroide di origine della rete, i percorsi di minimo costo per raggiungere i centroidi di destinazione. Tale metodo viene utilizzato sia come scelta iniziale del percorso da assegnare a ogni veicolo e sia durante la guida nel caso di simulazioni con cambio di percorso dinamico. Per quanto riguarda la struttura dei dati, l’esecuzione dell’algoritmo di Dijkstra richiede 4 variabili da aggiornare ad ogni iterazione, ossia:
· un elenco di etichette e;
· una lista L di dimensione variabile (al massimo N), detta anche serbatoio;
· un vettore di costi c (di dimensione N);
· un vettore di predecessori p (di dimensione N).
Il primo step dell’algoritmo (inizializzazione) consiste nel tracciamento di archi fittizi di costo infinito che congiungono il nodo radice alle altre destinazioni. Ad ogni iterazione viene estratto dalla lista il primo nodo contenuto nella lista. Per ogni nodo j-esimo appartenente alla stella in uscita dal nodo corrente i-esimo, viene verificata la condizione di Bellmann j i ij c > c + c , dove:
· cj costo corrente per raggiungere il nodo j dal nodo radice;
· ci costo corrente per raggiungere il nodo i dal nodo radice;
· cij costo dell’arco ij.
Se la condizione di Bellmann è verificata si procede all’etichettatura del nodo j-esimo con il nuovo valore ej = cj. I costi ed i predecessori relativi ai nodi etichettati verranno aggiornati nel corso della medesima iterazione. Infine, si procede all’inserimento nella lista L dei nodi etichettati (sempre che non siano già contenuti nella lista), riordinando la lista stessa per costi crescenti. Una volta esaminata la stella in uscita dal nodo corrente, provveduto all’etichettatura ed all’aggiornamento della lista e dei vettori p e c, si rimuove il nodo corrente da L e si passa all’iterazione successiva. L’algoritmo ha termine quando la lista è vuota: tutti i nodi del grafo sono stati esaminati.
CAPITOLO 5 – SAFETY AUDIT
Il Safety Audit è un approccio pianificato, indipendente, documentato e sistematico per determinare il livello di successo del sistema di gestione della sicurezza. Esso implica la raccolta di dati, la loro elaborazione ed analisi e il confronto degli stessi con gli obiettivi di sicurezza che l’infrastruttura deve rispettare. In particolare, questa procedura consente di identificare i problemi di sicurezza emergenti prima che essi diventino potenzialmente pericoli per gli utenti. E’ possibile effettuare diverse tipologie di analisi:
· Audit di conformità: viene anche chiamato condition inspection. Questo tipo di audit si concentra maggiormente sulle condizioni non sicure, considerando tre fattori: conformità, tenuta dei registri e addestramento.
· Audit del programma: questo tipo di audit pesa la strategia dei programmi di sicurezza e la sua attuazione.
· Audit del sistema di gestione: questo tipo di audit valuta l'efficacia e l'impegno della direzione in termini di conformità alla sicurezza, programmi, misure di controllo dei rischi e coinvolgimento dei dipendenti.
Ogni singolo difetto rappresenta quindi un insieme di scenari esistenti riferiti al sito analizzato che costituiscono dei potenziali generatori di danno per insicurezza stradale. Per ogni scenario è fornita una sua rappresentazione emblematica con rilievo fotografico con una sintetica descrizione del problema analizzato nell’ottica delle condizioni di decadimento delle prestazioni in termini di sicurezza stradale rispetto ad uno scenario ideale di sicurezza infrastrutturale. Ogni caso di analisi è caratterizzato da: · descrizione del problema in cui si fornisce una descrizione sintetica riferita al tipo di danno che può essere provocato e dei difetti che lo determinano o aggravano
· rilievo fotografico con riferimento ad uno o più casi rappresentativi del problema descritto
Per agevolare la localizzazione dei casi descritti, ogni punto del tracciato campionato è stato localizzato in coordinate GPS ( WGS-84 ).
5.1 Safety Audit 2010
|
SEFTY AUDIT STATO 2018 (2010) |
|
id. |
M1 |
||
|
PROBLEMA |
Muretto a ridosso della carreggiata |
|
|||
|
LATITUDINE |
39,036111° |
||||
|
LONGITUDINE |
17,067627° |
||||
|
STRADA |
Strada Statale 106 Jonica |
||||
|
DESCRIZIONE |
|||||
|
Il muretto in cls si presenta in prossimità della linea di demarcazione destra della carreggiata privo di sistemi di ritenuta atti a prevenire gli urti con essa |
|||||
|
SEFTY AUDIT STATO 2018 (2010) |
|
id. |
M2 |
||
|
PROBLEMA |
Muro di sostegno a ridosso della carreggiata |
|
|||
|
LATITUDINE |
39,036508° |
||||
|
LONGITUDINE |
17,069875° |
||||
|
STRADA |
Strada Statale 106 Jonica |
||||
|
DESCRIZIONE |
|||||
|
Il muro di sostegno a gabbioni si presenta a ridosso della carreggiata separato da essa da un cordolo in cls di altezza 1 m |
|||||
|
SEFTY AUDIT STATO 2018 (2010) |
|
id. |
M3 |
||
|
PROBLEMA |
Muretto in cls a ridosso della carreggiata |
|
|||
|
LATITUDINE |
39,037641° |
||||
|
LONGITUDINE |
17,071113° |
||||
|
STRADA |
Strada Statale 106 Jonica |
||||
|
DESCRIZIONE |
|||||
|
Il muretto in cls alto 1 m si presenta ad una distanza di 1,90 m dalla linea di demarcazione della carreggiata con totale assenza di sistemi di ritenuta atti a prevenire gli urti con essa |
|||||
|
SEFTY AUDIT STATO 2018 (2010) |
|
id. |
M4 |
||
|
PROBLEMA |
Muretto a ridosso della carreggiata |
|
|||
|
LATITUDINE |
39,045869° |
||||
|
LONGITUDINE |
17,726361° |
||||
|
STRADA |
Strada Statale 106 Jonica |
||||
|
DESCRIZIONE |
|||||
|
Il muretto in cls alto 1 m si presenta ad una distanza di 60 cm dal margine destro della carreggiata con assenza di sistemi di ritenuta atti a prevenire urti con esso |
|||||
|
SEFTY AUDIT STATO 2018 (2010) |
|
id. |
M5 |
||
|
PROBLEMA |
Muretto sporgente |
|
|||
|
LATITUDINE |
39,046763° |
||||
|
LONGITUDINE |
17,072475° |
||||
|
STRADA |
Strada Statale 106 Jonica |
||||
|
DESCRIZIONE |
|||||
|
Il muretto il cls delimita la carreggiata dall’ ingresso al lotto attiguo ,esso risulta sporgente nella parte inferiore e privo di sistemi di ritenuta atti a prevenire gli urti con essa |
|||||
|
SEFTY AUDIT STATO 2018 (2010) |
|
id. |
M6 |
||
|
PROBLEMA |
Muretto affiorante |
|
|||
|
LATITUDINE |
39,043211° |
||||
|
LONGITUDINE |
17,068516° |
||||
|
STRADA |
Via Nazionale |
||||
|
DESCRIZIONE |
|||||
|
Il muretto in cls di altezza 60 cm a ridosso della linea di demarcazione della carreggiata ricoperto da vegetazione risulta inadeguato a svolgere il compito di barriera con la fiumara sottostante |
|||||
|
SEFTY AUDIT STATO 2018 (2010) |
|
id. |
G1 |
||
|
PROBLEMA |
Guardrail sporgente |
|
|||
|
LATITUDINE |
39,043538° |
||||
|
LONGITUDINE |
17,069530° |
||||
|
STRADA |
Via Nazionale |
||||
|
DESCRIZIONE |
|||||
|
Il sistema di ritenuta risulta sporgente sulla linea di demarcazione della carreggiata |
|||||
5.2 Safety Audit 2018
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
M1 |
||
|
PROBLEMA |
Muro a ridosso della carreggiata |
|
||
|
LATITUDINE |
39,034473° |
|||
|
LONGITUDINE |
17,067627° |
|||
|
STRADA |
Strada Statale 106 Jonica |
|||
|
DESCRIZIONE |
||||
|
Il muro di sostegno in cls armato rivestito presenta una sporgenza a spigolo vivo ed una totale assenza di elementi di ritenuta atti a prevenire gli urti con essa |
||||
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
M2 |
||
|
PROBLEMA |
Muro di sostegno a ridosso della carreggiata |
|
||
|
LATITUDINE |
39,036509° |
|||
|
LONGITUDINE |
17,069874° |
|||
|
STRADA |
Strada Statale 106 Jonica |
|||
|
DESCRIZIONE |
||||
|
Il muro di sostegno a gabbioni si presenta a ridosso della carreggiata separato da essa da un cordolo in cls di altezza 1 m |
||||
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
M3 |
||
|
PROBLEMA |
Muretto in cls a ridosso della carreggiata |
|
||
|
LATITUDINE |
39,037642° |
|||
|
LONGITUDINE |
17,071115° |
|||
|
STRADA |
Strada Statale 106 Jonica |
|||
|
DESCRIZIONE |
||||
|
Il muretto in cls alto 1 m si presenta ad una distanza di 1,90 m dalla linea di demarcazione della carreggiata con totale assenza di sistemi di ritenuta atti a prevenire gli urti con essa |
||||
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
M4 |
||
|
PROBLEMA |
Muretto a ridosso della carreggiata |
|
||
|
LATITUDINE |
39,045869° |
|||
|
LONGITUDINE |
17,072635° |
|||
|
STRADA |
Strada Statale 106 Jonica |
|||
|
DESCRIZIONE |
||||
|
Il muretto in cls alto 1 m si presenta ad una distanza di 60 cm dal margine destro della carreggiata con assenza di sistemi di ritenuta atti a prevenire urti con esso |
||||
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
M5 |
||
|
PROBLEMA |
Muretto sporgente |
|
||
|
LATITUDINE |
39,046763° |
|||
|
LONGITUDINE |
17,072475° |
|||
|
STRADA |
Strada Statale 106 Jonica |
|||
|
DESCRIZIONE |
||||
|
Il muretto il cls delimita la carreggiata dall ingresso al lotto attiguo, esso risulta sporgente nella parte inferiore e privo di sistemi di ritenuta atti a prevenire gli urti con essa |
||||
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
M6 |
||
|
PROBLEMA |
Muretto affiorante |
|
||
|
LATITUDINE |
39,043212° |
|||
|
LONGITUDINE |
17,068516° |
|||
|
STRADA |
Strada Statale 106 Jonica |
|||
|
DESCRIZIONE |
||||
|
Il muretto in cls di altezza 60 cm a ridosso della linea di demarcazione della carreggiata ricoperto da vegetazione risulta inadeguato a svolgere il compito di barriera con la fiumara sottostante |
||||
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
G1 |
||
|
PROBLEMA |
Guardrail sporgente |
|
||
|
LATITUDINE |
39,039199° |
|||
|
LONGITUDINE |
17,072353° |
|||
|
STRADA |
Strada Statale 106 Jonica |
|||
|
DESCRIZIONE |
||||
|
Il sistema di ritenuta si presenta sporgente verso il margine della carreggiata a causa di un elevato tasso di deterioramento |
||||
|
SEFTY AUDIT STATO 2018 (2018) |
id. |
G2 |
||
|
PROBLEMA |
Guardrail sporgente |
|
||
|
LATITUDINE |
39,043539° |
|||
|
LONGITUDINE |
17,568516° |
|||
|
STRADA |
Via Nazionale |
|||
|
DESCRIZIONE |
||||
|
Il sistema di ritenuta risulta sporgente sulla linea di demarcazione della carreggiata |
||||
CAPITOLO 6 - Risultati
Attraverso il Software di micro-simulazione Tritone ed attraverso il Software Zombie Drive è stato possibile non solo provvedere al calcolo ed alla valutazione delle prestazioni in fase di esercizio ma anche alle condizioni di criticità relative alla sicurezza dell’infrastruttura. Una volta ottenuti i risultati delle simulazioni si è provveduto alla loro elaborazione attraverso Excel al fine di evidenziare nel miglior modo possibile quale scenario, tra quello relativo all’anno 2010 e quello 2018, desse risultati migliori in termini di parametri riguardanti la sicurezza stradale.
6.1 Risultati Prestazionali della rete
Tali risultati sono stati ottenuti attraverso la simulazione di scenari virtuali effettuata dal software Tritone.
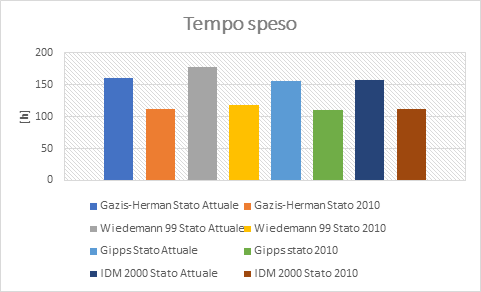
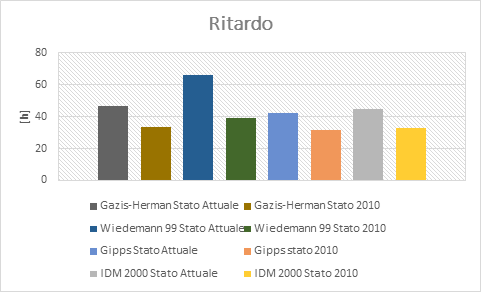
Si definisce tempo speso, la somma di tutti i tempi di percorrenza dei singoli veicoli, mentre viene definito ritardo la somma del tempo perso dai singoli veicoli nel percorrere la rete in condizioni di traffico reale alla velocità desiderata. Scendendo nel dettaglio è possibile notare come i risultati ottenuti dai vari modelli di simulazione relativamente al tempo speso risultano superiori per lo scenario 2018. Analizzando successivamente i risultati relativi al Ritardo, è evidente come il modello Wiedemann 99 risulta superiore agli altri in quanto si basa su una distanza tra i veicoli inferiore agli altri modelli..
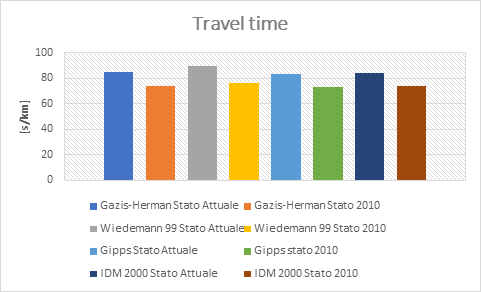
Dai dati elaborati risulta un aumento del Travel Time per lo scenario 2018 a causa delle modifiche apportate alla rete, tuttavia l’aumento risulta proporzionale per ogni modello utilizzato risultando massimo per il modello Wiedemann 99.
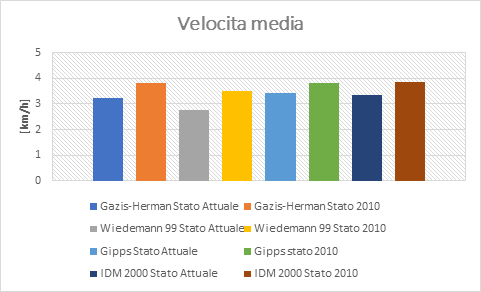
Analizzando il grafico della velocità media, si può osservare come tutti i modelli, in riferimento allo scenario 2018 risultano inferiori a quello del 2010. Ciò è dovuto in particolar modo all’introduzione della nuova rampa di accesso-egresso collocata ad EST.
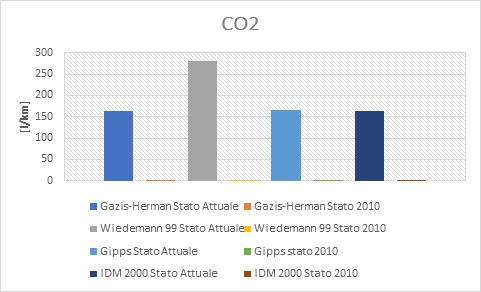
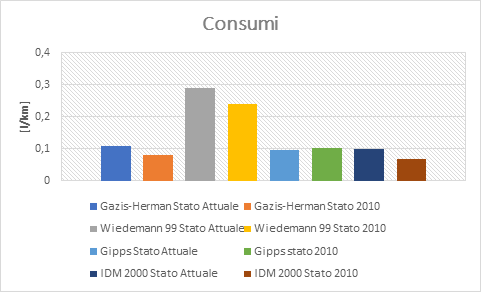
Si può osservare come, nell’ambito della rappresentazione del grafico di CO2 e dei consumi, i modelli tendono a convergere verso un valore costante sia per quanto riguarda lo scenario al 2010 che per quello 2018, ad eccezione per il risultato ottenuto con il modello Wiedemann 99 relativo allo scenario 2010 che risulta essere nettamente maggiore.
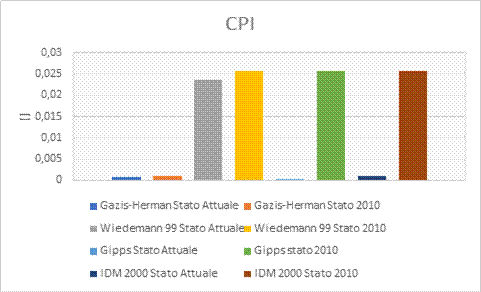
I valori di CPI risultano bassi per tutti i modelli e scenari, raggiungendo un massimo valore di 0.26.Dai grafici è possibile notare come i valori relativi ai modelli Wiedemann 99 risultino entrambi superiori alla media.
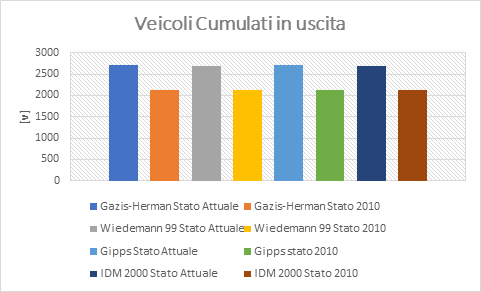
Dal grafico si nota come i modelli gestiscono la rete in modo proporzionale
6.2 Analisi SSAM
Mediante la funzione aggiuntiva implementata in TRITONE è stato possibile effettuare l’analisi SSAM in automatico, la quale ci ha permesso di analizzare gli indicatori TTC, PET, DeltaS e numero di Conflitti, secondo le prescrizioni di questo algoritmo. Di seguito sono riportati i risultati ottenuti
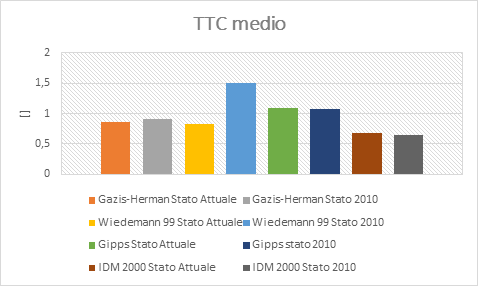
Questo grafico ci consente di evidenziare come la rete risulta essere critica in ambito di sicurezza stradale, in quanto, nonostante sono stati utilizzati diversi modelli di car-following, i risultati sono tutti sotto la soglia critica stimata da diversi autori (Hirst e Graham 3,5 secondi, Van Der Horst 4 secondi), sia per l’anno 2010 che 2018
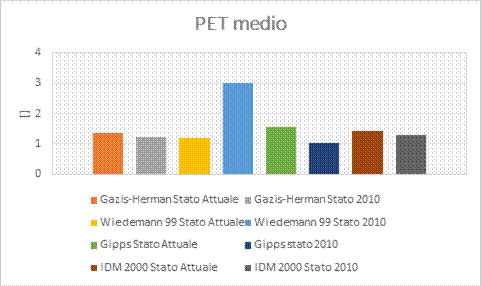
Per quanto riguarda l’analisi del PET, si può notare che il valore migliore risulta essere quello ottenuto medianti le simulazioni effettuate con Gipps anche se risulta essere un valore al di sotto del valore critico riportato da alcuni autori.
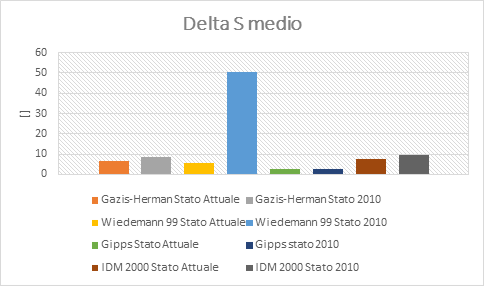
Il deltaS è la differenza dei vettori velocità, con il modello Wiedemann 99 per lo scenario 2010 risultano collisioni più pericolose per entrambi gli scenari.
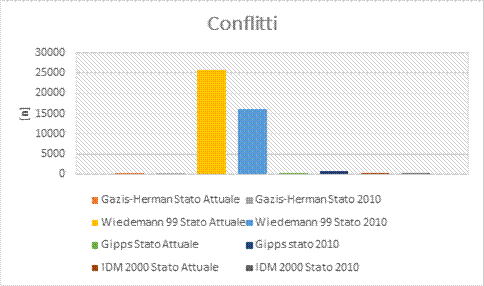
Il grafico dei conflitti evidenzia come con Wiedemann99 i conflitti risultano essere maggiori degli altri modelli, mentre gli altri modelli restituiscono valori più bassi. Nasce qui, analizzando i conflitti totali, il problema che in tutti i casi non si riesce a capire quale sia lo scenario migliore e quale il peggiore tra il 2010 o il 2018 a parità di modello utilizzato. Sezionando il grafico ad un valore indicativo di 500 è possibile notare :
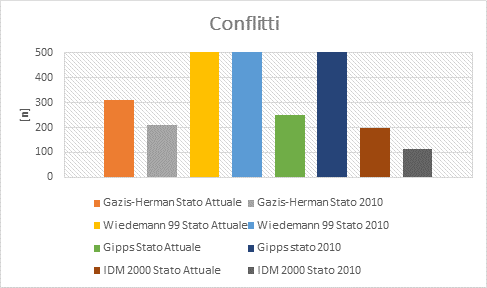
6.3 Procedura Zombie Drive
Una volta simulati attraverso Tritone gli scenari riguardanti la rete in esercizio per tutti i modelli esplicitati in precedenza si è provveduto all’estrazione dei file traiettoria che rappresentano i punti assunti dal veicolo durante il moto istante per istante. Successivamente essi ed i sistemi di ritenuta elastici ed inelastici sono stati importati in Zombie Drive attraverso il menù Main ed una volta impostati tempo massimo di distrazione e scala grafica è stato possibile far partire la simulazione dal menù Analysis
Fig.6.3 Zombie Drive
Una volta terminate le simulazioni in riferimento alle due condizioni poste sotto osservazione 2010 e stato 2018 il software fornisce come output attraverso dati e mappe tematiche :
· Aree di Collisione
· Aree di Collisione Veicolo-Ostacolo
· Aree di Collisione Veicolo-Veicolo
· Aree di Massima Energia
· Area di Massima Energia impatti Veicolo-Ostacolo
· Area di Massima Energia impatti Veicolo-Veicolo
· Aree di Energia Media Veicolo-Veicolo
· Aree di Energia Media Veicolo-Ostacolo
· Aree soggette a rischio feriti
· Aree soggette a rischio feriti impatti Veicolo-Veicolo
· Aree soggette a rischio feriti impatti Veicolo-Ostacolo
· Aree soggette a rischio morte
· Aree soggette a rischio morte impatti Veicolo-Veicolo
· Aree soggette a rischio morte impatti Veicolo-Ostacolo
· Aree di velocita media
· Collisioni
· Occorrenze per distrazione
· Occorrenze per energia
· Occorrenze per gravità
· Tipologia di sbandamenti
In seguito, sono riportati i grafici più significativi derivanti dall’elaborazione:
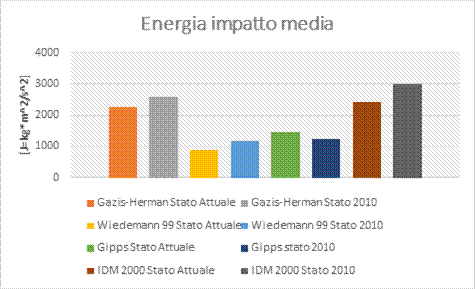
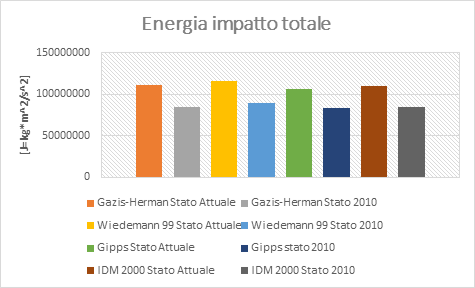
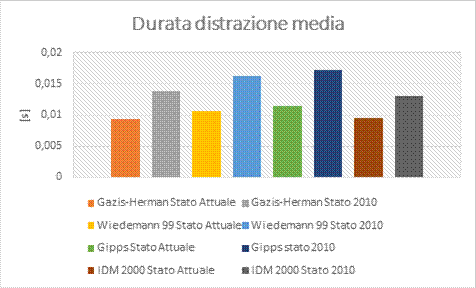
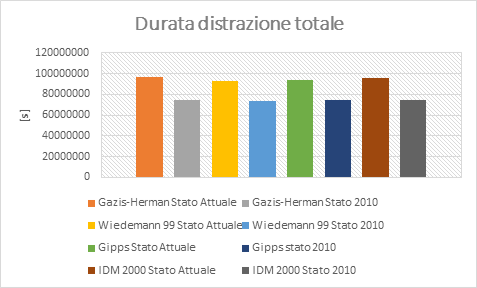
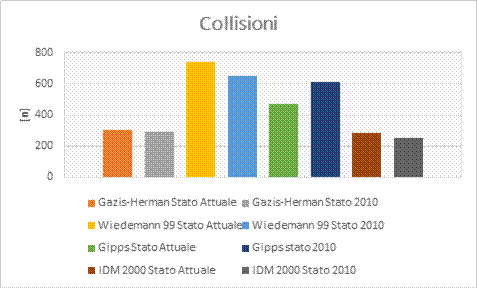
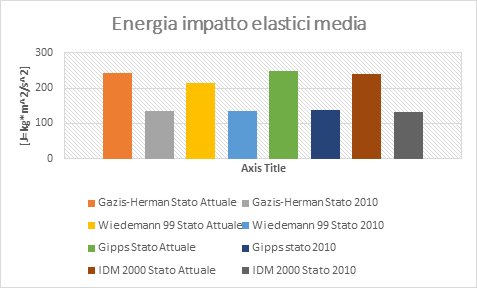
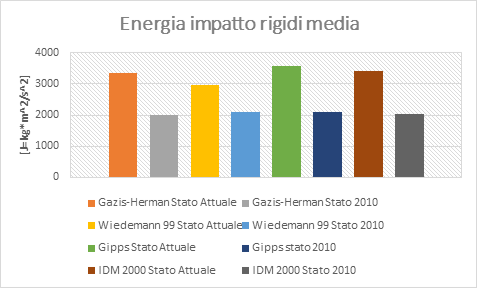
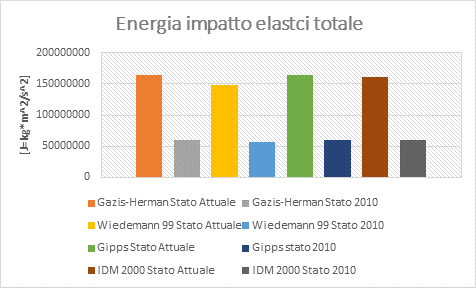
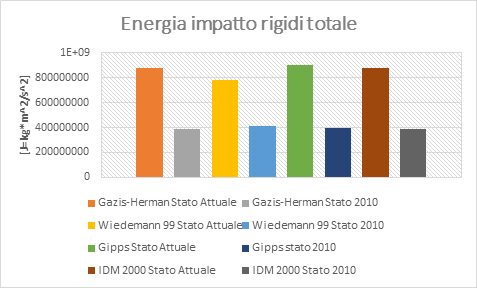
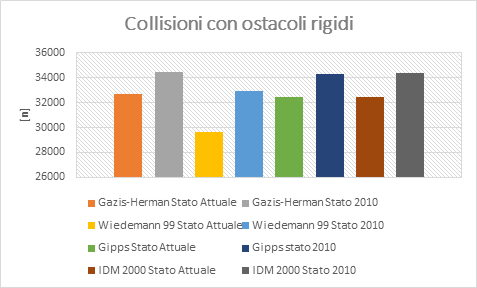
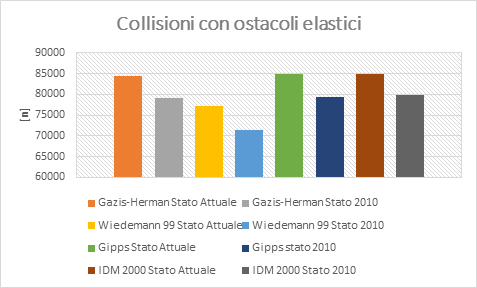
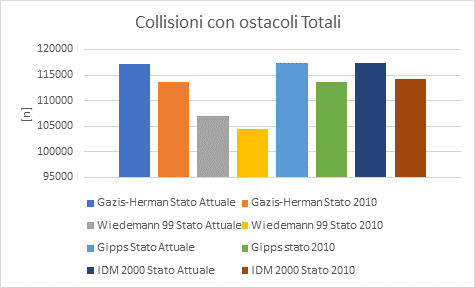
6.4 Confronto SAAM Zombie Drive
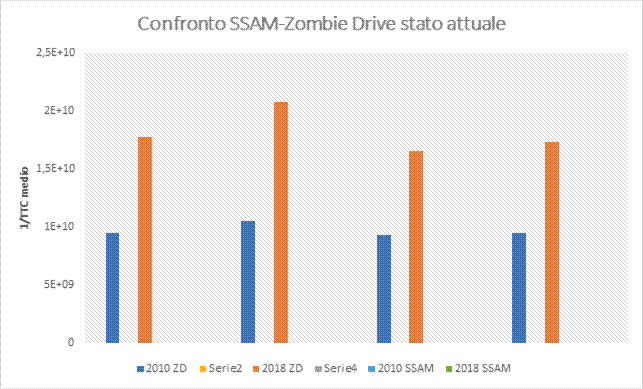
Dall’analisi del grafico di confronto tra il principale indicatore fornito da Zombie Drive ovvero l’energia totale d’impatto, ed il reciproco del valore principale fornito da SSAM ovvero il TTC è immediato notare come l’introduzione della nuova rampa l’immissione ha provocato un abbassamento del livello di sicurezza. Analizzando i valori di energia si vede come l’aumento della stessa è evidenziato in tutti i modelli con picco maggiore per quanto riguarda il modello Wiedemann 99 con un incremento di 10219776410 kg/m^2/s^2.Prendendo in considerazione invece i valori derivanti dall’analisi SSAM è possibile notare come la diminuzione della sicurezza per lo stato 2018 viene segnalata esclusivamente nei modelli di Gazis-Herman e Wiedemann99 con un incremento del valore rispettivamente di 0.06 e 0.53. Nel modello di Gipps il valore 1/TTC 2018 risulta inferiore di quello 2010 di 0.0076 e nell’ IDM 2000 di 0.095. In conclusione dall’osservazione è possibile affermare come il software Zombie Drive fornisce con una precisione del 100% lo scenario più pericolo al contrario dell’analisi SSAM che fornisce una percentuale del 50%
6.5 Distribuzione dell’energia di collisione
Durante il processo di analisi con Zombie Drive si sono valutate le occorrenze, ovvero per ogni collisione è stato segnato il suo valore come mostrato in figura:
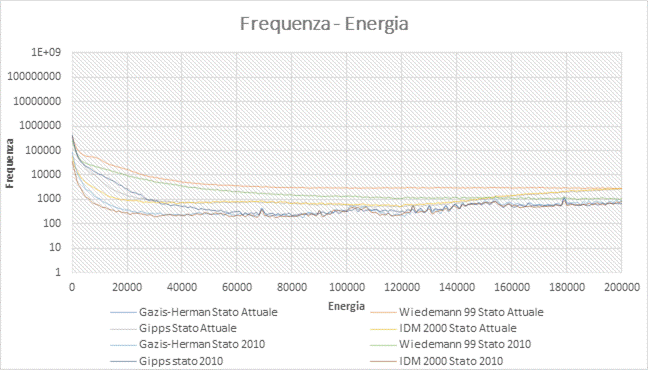
Analizzando il grafico che mette in relazione la Frequenza con l’Energia, possiamo notare come tutte le frequenze hanno lo stesso andamento. Si evidenziano molti valori bassi e pochissimi valori alti. Sono state individuate tre soglie sull’asse dell’Energia, la prima a 100000, la seconda a 250000 e la terza a 500000, che ci hanno permesso di definire gli spazi con eventi simili, ovvero la prima parte con energia molto bassa evidenzia collisioni lievi, la seconda parte collisioni intermedie che potrebbero non indurre a morti ma solo danni a cose ed una terza parte, con energia superiore a 500000, dove invece si dovrebbero verificare danni a persone.
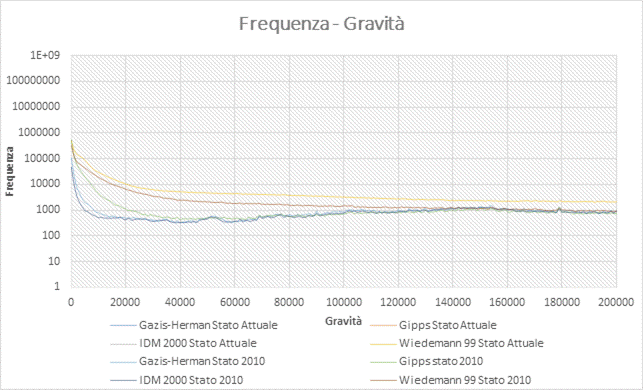
Analizzando il grafico che mette in relazione la Frequenza con la Gravità, possiamo notare come tutte le frequenze anche in questo caso hanno lo stesso andamento. Si evidenziano molti valori bassi e pochissimi valori alti. Sono state individuate tre soglie sull’asse delle gravità, la prima a 100000, la seconda a 250000 e la terza a 500000, che ci hanno permesso di definire gli spazi con eventi simili, ovvero la prima parte con gravità molto bassa evidenzia collisioni lievi , la seconda parte collisioni intermedie che potrebbero non indurre a morti ma solo danni a cose ed una terza parte, con gravità superiore a 500000, dove invece si dovrebbero verificare danni a persone in quanto la gravità della collisione è nettamente elevata.
CAPITOLO 7 - Analisi in dettaglio dei Black-Point
7.1 Aree di Collisione Veicolo-Veicolo
|
Modello Gazis-Herman STATO 2010 |
Modello Gazis-Herman STATO 2018 |
|
|
|
7.2 Aree di Energia Totale
|
Modello Gipps STATO 2010 |
Modello Gipps STATO 2018 |
|
|
|
|
Modello Wiedemann 99 STATO 2010 |
Modello Wiedemann 99 STATO 2018 |
|
|
|
|
Modello IDM 2000 STATO 2010 |
Modello IDM 2000 STATO 2018 |
|
|
|
|
Modello Gazis-Herman STATO 2010 |
Modello Gazis-Herman STATO 2018 |
|
|
|
|
Modello Gipps STATO 2010 |
Modello Gipps STATO 2018 |
|
|
|
|
Modello Wiedemann 99 STATO 2010 |
Modello Wiedemann 99 STATO 2018 |
|
|
|
|
Modello IDM 2000 STATO 2010 |
Modello IDM 2000 STATO 2018 |
|
|
|
7.3 Aree di Energia Impatto Veicolo-Veicolo Totale
|
Modello Gazis-Herman STATO 2010 |
Modello Gazis-Herman STATO 2018 |
|
|
|
|
Modello Gipps STATO 2010 |
Modello Gipps STATO 2018 |
|
|
|
|
Modello Wiedemann 99 STATO 2010 |
Modello Wiedemann 99 STATO 2018 |
|
|
|
|
Modello IDM 2000 STATO 2010 |
Modello IDM 2000 STATO 2018 |
|
|
|
7.4 Collisioni
|
Modello Gazis-Herman STATO 2010 |
Modello Gazis-Herman STATO 2018 |
|
|
|
|
Modello Gipps STATO 2010 |
Modello Gipps STATO 2018 |
|
|
|
|
Modello Wiedemann 99 STATO 2010 |
Modello Wiedemann 99 STATO 2018 |
|
|
|
|
Modello IDM 2000 STATO 2010 |
Modello IDM 2000 STATO 2018 |
|
|
|
CAPITOLO 8 - Conclusioni
Il seguente lavoro di tesi ha analizzato il tratto della Strada Statale 106 Jonica nell’area di S.Anna (KR), confrontando le condizioni di sicurezza dello scenario 2010 con quelle dello scenario 2018. In prima istanza si è provveduto alla modellizzazione ed alla simulazione in esercizio della rete, considerando le modifiche apportate negli anni ed in particolare la nuova rampa d’accesso lato EST attraverso il software di micro-simulazione Tritone. È stata utilizzata la teoria dell’inseguitore ovvero il Car - following, che simula il comportamento di un veicolo influenzato esclusivamente dal veicolo che lo precede lungo la medesima corsia. I modelli di car - following utilizzati sono stati modelli basati sulla classica teoria delle code e modelli basati sui fattori psico-fisici dei guidatori. In questa tesi si è valutata la capacità, di ciascun modello di car - following utilizzato, di produrre stime ragionevoli in termini di indicatori di sicurezza stradale (conflitti totali, media TTC, PET, ecc.) e in termini di collisioni mediante il calcolo dell’energia di collisione. Successivamente si è provveduto al caricamento delle traiettorie e dei sistemi di ritenuta sul software Zombie Drive, sviluppato dall’Ing Giofrè, ed all’effettuazione delle simulazioni. Una volta ottenuti i dati relativi alle collisioni, alle frequenze, alle energie d’impatto, alla distrazione ed alla gravità è stato possibile elaborarli attraverso Excel e confrontarli ai dati relativi all’analisi SSAM. Da tale confronto è emerso che l’introduzione della nuova rampa d’accesso ha diminuito gli indici di sicurezza, ma che solo attraverso l’utilizzo dell’software Zombie Drive è possibile determinarlo. Il software a differenza dell’analisi SSAM ha segnalato in tutti i modelli relativi allo stato 2018 un aumento di energia ottenendo quindi un grado di precisione del’ 100% sui quattro modelli analizzati. L’ analisi SSAM ha evidenziato lo stesso dato soltanto in due modelli sui quattro analizzati ottenendo quindi un’accuratezza del dato del 50%.
Bibliografia
Allen, B.L., Shin, B.T. e Cooper, D. J. 1978. “Analysis of Traffic Conflicts and Collision.”
Archer, J. 2005a. “Indicators for Traffic Safety Assessment and Prediction and Their Application in Micro-Simulation Modelling: A Study of Urban and Suburban Intersections.”
Archer, J. 2005b. “Methods for the Assessment and Prediction of Traffic Safety at Urban Intersection and Their Application in Microsimu-Lation Modeling.” Royal Institute of Technolo-gy, Sweden.
Astarita, Vittorio and Vincenzo Giofré. 2018. “From Traffic Conflict Simulation to Traffic Crash Simulation: Introducing Traffic Safety Indicators Based on the Explicit Simulation of Potential Driver Errors.”
Astarita, Vittorio, Vincenzo Pasquale Giofrè, Giuseppe Guido, Alessandro Vitale, D. C. Festa, R. Vaiana, T. Iuele, D. W. E. Mongelli, Daniele Rogano, and Vincenzo Gallelli. 2017. “New Features of Tritone for the Evaluation of Traffic Safety Performances.” Aiit International Congress on Transport Infrastructure and Systems (Tis 2017), Rome, Italy, 10-12 April 625–32.
Cavallo, V e Laurent, M. 1988. “Visual Information and Skill Level in Time-to-Collision Estimation.”
Chandler, R. E., R. Herman, and E. W. Montrol. 1958. “Traffic Dynamics: Studies in Car-Following.” Operation Research 6(2):118–65.
Farber, B. “Designing a distance warning system from the user point of view”. APSIS report, Glonn-Haslach, 1991.
Federal Highway Administration. “Surrogate Safety Assessment Model and Validation: Final Report. s.l.”: Federal Highway Administration. FHWA-HRT-08-051.
Fellendorf, Martin and Peter Vortisch. 2010. “Microscopic Traffic Flow Simulator VISSIM.” in International Series in Operations Research and Management Science.
Fritzsche, Hans-thomas and Daimler-benz Ag. 1994. “A Model for Traffic Simulation.” Traffic Engineering and Control 35:317–21.
Gazis, Denos C., Robert Herman, and Renfrey B. Potts. 1959. “Car-Following Theory of Steady-State Traffic Flow.” Http://Dx.Doi.Org/10.1287/Opre.7.4.499.
Gazis, Denos C., Robert Herman, and Richard W. Rothery. 1961. “Nonlinear Follow-the-Leader Models of Traffic Flow.” Operations Research.
Gettman, Douglas, Tarek Sayed, Lili Pu, and Steve Shelby. 2008. “Surrogate Safety Assessment Model and Validation.” Fhwa-Hrt-08--51.
Giofrè, V. P., M. Maciejewski, A. Merkisz-Guranowska, B. Piątkowski, and V. Astarita. 2013. “Real Road Network Application of a New Microsimulation Tool: TRITONE.” Archives of Transport 27–28(3–4).
Giofrè, Vincenzo Pasquale and Vittorio Astarita. 2014. “Tritone - Un Microsimulatore per La Sicurezza Stradale.” Strade & Autostrade 4(106):158–59.
Giofrè, Vincenzo Pasquale, M. Maciejewski, A. Merkisz-Guranowska, Vittorio Astarita, and B. Piątkowski. 2015. “TRITONE Studio Di Vari Modelli Di Car-Following.” EDI-CEM Srl - Strade & Autostrade 1(109):148–51.
Gipps, P. G. 1981. “A Behavioural Car-Following Model for Computer Simulation.” Transportation Research Part B.
Hayward, John C. 1972. “Near-Miss Determination through Use of a Scale of Danger.” Highway Res. Rec.
Herman, R. and R. W. Rothery. 1969. “Frequency and Amplitude Dependence of Disturbance in a Traffic Stream.” 4° International Symposium on the Theory of Traffic Flow, Germany.
Herman, Robert, Elliott W. Montroll, Renfrey B. Potts, and Richard W. Rothery. 1959. “Traffic Dynamics: Analysis of Stability in Car Following.” Operations Research.
Hirst S. e Graham, R. 1997. “The Format and Presentation of Collision Warnings.”
Hogema, J.H., Janssen, W.H., Coemet, M. e Soeteman, H. J. 1996. “‘Effects of Intelligent Cruise Control on Driving Behaviour, a Simulator Study.’”
Incidenti Stradali 2017. “Istat”
Van der Horst, R. and J. Kraay. 1986. “The Dutch Conflict Observation Technique - DOCTOR.” in Traffic Conflicts and Other Intermediate Measures in Safety Evaluation, Budapest, Hungary.
Hydén, C. 1996. “Traffic Conflicts Technique: State-of-the-Art.” in Topp H.H. (Ed.), (1996). Traffic Safety Work with Video-Processing. University Kaiserslautern. Transportation Department, 1996, Green Series No.43, Kaiserslauten, Germany.
Hyden, Christer. 1987. “The Development of a Method for Traffic Safety Evaluation: The Swedish Traffic Conflict Technique.” Bulletin 70, Lund University of Technology, Lund.
Maretzke, J e Jacob, U. 1992. “‘Distance Warning and Control as a Means of Increasing Road Safety.’” Pp. 105–14 in.
Nilsson. 1989. “Safety for Different Road-User Groups. Data Collection, Problems, Consequences and Costs”.”
Treiber, Martin, Ansgar Hennecke, and Dirk Helbing. 2000. “Microscopic Simulation of Congested Traffic.” Traffic and Granular Flow ’99.
VISSIM. 2012. VISSIM 5.40-01, User Manual, Planung Transport Verkehr AG, Karlsruhe, Germany.
Wiedemann, Rainer. 1974. “Simulation Des Straßenverkehrsflusses, Schriftenreihe Des Instituts Für Verkehrswesen Der Universität Karlsruhe, Germany.”
Wiedemann, Rainer. 1991. Modelling of RTI-Elements on Multi-Lane Roads.